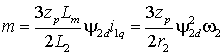2.2.1.2 Модель АД, управляемого током статора

В синхронной системе координат , ориентированной по магнитному полю ротора (), уравнение ротора имеет вид

В это уравнение в качестве переменной входит неконтролируемый ток ротора. Для исключения  из выражения  для потокосцепления найдем 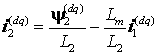. Тогда, подставляя его в исходное выражение и опуская далее индексы системы координат, получим

.

Преобразуем это уравнение по Лапласу и введем в него электромагнитную постоянную времени ротора ,

.

Отсюда найдем проекции вектора тока статора с учетом того, что

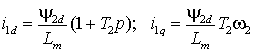                           (1)

а также потокосцепление и угловую частоту ротора

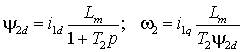.                            (2)

Таким образом, с помощью продольной проекции тока статора  можно независимо управлять потокосцеплением ротора и передаточная функция этого канала соответствует апериодическому звену с постоянной времени равной постоянной времени ротора. Продольная составляющая тока статора  играет в АД роль тока возбуждения машины постоянного тока или синхронной машины. Поперечная проекция  при постоянном потоке ротора позволяет безинерционно управлять частотой ротора .

Подставляя  в выражение электромагнитного момента, получим

(3)

т.е. частота ротора  или поперечная составляющая тока статора  при заданном потокосцеплении определяют электромагнитный момент АД. Следовательно, составляющая  является аналогом тока якоря машины постоянного тока.

Подстановкой  выражение (3) можно преобразовать и получить уравнение механической характеристики вида

,

где 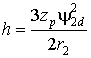  жесткость характеристики, определяемая величиной потокосцепления  и активным сопротивлением ротора . Выражение для жесткости идентично жесткости характеристики ДПТ, если в нем под сопротивлением якоря понимать . При  механическая характеристика линейна и по характеру полностью соответствует характеристике ДПТ с независимым возбуждением.

Из выражений (2.14) можно определить электромеханическую характеристику АД . Для статического режима справедливо

,

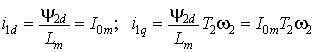где  – амплитуда тока холостого хода. Отсюда с учетом

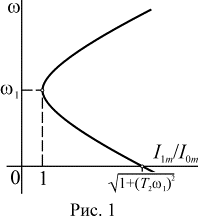
. Эта характеристика представляет собой параболу симметричную относительно частоты холостого хода (рис. 1), изменение которой будет приводить к параллельному смещению кривой. Увеличение мощности АД обычно соответствует увеличению постоянной времени ротора , что будет приводить к росту относительного пускового тока  и в целом к сближению ветвей параболы.

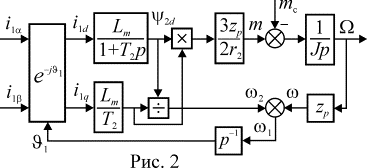Выражения (2)-(3) совместно с уравнением движения электропривода позволяют построить структурную схему АД представленную на рисунке 2. Входными величинами здесь являются проекции вектора тока статора  и , а также момент сопротивления на валу АД . Однако в реальном АД ток статора формируется в неподвижной системе координат  в виде синусоидальных функций времени, а ток во вращающихся координатах  получается в результате преобразования , где  текущий угол системы координат, определяемый как результат интегрирования угловой частоты статора . Функцию эту выполняет внутренний блок вращения вектора тока или ротатор ( на рис. 2).

Выражения (1) и приведенная на рисунке 2 структурная схема соответствуют проекциям вектора тока на ортогональные оси системы координат, что эквивалентно двухфазной машине. В действительности большинство АД трехфазные, поэтому в случае необходимости использования при анализе фазных токов уравнения и структурная схема должны быть дополнены безинерционным блоком преобразования числа фаз.