2.2.1.1 Выбор уравнения электромагнитного момента АД и системы координат

Для построения систем векторного управления АД могут быть использованы любые пары векторов, с помощью которых можно представить электромагнитный момент обобщенной электрической машины. Однако от выбора векторов в значительной мере зависит степень сложности системы. Желательно, чтобы величины, представленные векторами в уравнении момента были наблюдаемы, т.е. чтобы их можно было непосредственно измерить и воздействовать на них при управлении моментом. У короткозамкнутого АД есть только две такие величины – это напряжение и ток статора, и только одна из них, а именно ток статора, может входить в уравнение момента. Тогда другой величиной может быть только ток ротора или какое-либо потокосцепление. Ток ротора принципиально ненаблюдаем, а устройства его идентификации по наблюдаемым параметрам сложны и ненадежны. Поэтому для выбора остаются три потокосцепления: статора, ротора и основное, т.е. магнитный поток в зазоре АД. Потокосцепление статора и рабочий поток АД можно непосредственно измерить и использовать этот сигнал в системе управления, что часто и делается при создании приводов высокого качества. В массовых же изделиях разработчики стараются использовать сигналы, доступные без установки датчиков, т.е. все те же ток и напряжение статора, по мгновенным значениям которых можно вычислить, например, потокосцепление статора как . Однако при выборе потокосцепления статора или основного потокосцепления передаточные функции системы управления получаются довольно сложными и мало подходящими для практического использования.

Простейший вид имеют уравнения электромагнитных процессов в АД в случае представления их через вектор потокосцепления ротора . То обстоятельство, что  невозможно измерить не является препятствием для выбора, т.к. магнитный поток ротора легко вычисляется по потоку статора или по рабочему потоку. Поэтому в дальнейшем мы ограничимся рассмотрением наиболее распространенных систем, использующих для регулирования электромагнитного момента ток статора и потокосцепление ротора и соответствующее уравнение момента.

Поскольку форма уравнений потокосцеплений инвариантна к выбору системы координат, то в произвольной системе  уравнение момента будет иметь вид

            (1)

Векторы  и  вращаются в пространстве с угловой частотой . Поэтому если для описания процессов выбрать неподвижную систему координат или систему координат, вращающуюся синхронно с ротором АД, то проекции векторов будут синусоидальными функциями времени и регулирование таких величин будет сложной технической задачей. В случае же выбора системы координат вращающейся в пространстве с синхронной частотой , проекции векторов будут постоянными величинами, и управление ими будет не сложнее, чем управление токами якоря и возбуждения машины постоянного тока.

Задачу управления можно еще более упростить, если совместить какую-либо ось системы координат с одним из двух векторов. Тогда проекция опорного вектора на эту ось будет равна его модулю, а другая проекция будет равна нулю. При этом в уравнении электромагнитного момента (1) исчезнет соответствующее слагаемое в правой части.

Таким образом, если для управления электромагнитным моментом АД выбрать векторы потокосцепления ротора и тока статора и синхронную систему координат , совместив ось  с вектором , то уравнение (1) примет вид

,                                             (2)

который в принципе ничем не отличается от соответствующего выражения для машины постоянного тока и основной задачей системы управления будет идентификация проекций  и . Если при этом построить управление так, чтобы потокосцепление ротора сохранялось во всех режимах постоянным, то регулирование момента АД будет осуществляться изменением поперечной составляющей тока статора , выполняющей в такой системе функцию тока якоря.

Следует заметить, что в ориентированной по магнитному полю системе координат не только исключается влияние продольной составляющей тока статора  на векторное произведение, т.е. на электромагнитный момент АД, но с помощью этой проекции становится возможным управлять магнитным потоком. Это объясняется с тем, что ток статора в короткозамкнутом АД определяет все процессы в машине и если одна из его компонент не влияет на момент, то она тем или иным способом должна быть связана с магнитным потоком. В то же время, система координат  ортогональна, поэтому изменение одной из проекций тока никоим образом не влияет на другую, и управление моментом и потоком может производиться независимо.

Таким образом, принцип трансвекторного управления заключается в раздельном управлении магнитным потоком и моментом АД с помощью независимых составляющих тока статора, соответствующих проекциям вектора тока на оси системы координат, ориентированной по направлению вектора магнитного потока.

Это определение полностью подходит и для ДПТ, если токи возбуждения и якоря объединить в вектор, представленный в системе координат, ориентированной по оси главных полюсов. Отличие АД от ДПТ заключается только в том, что в АД система координат вращается вместе с потоком, а в ДПТ она неподвижна. Реальные же токи статора АД протекают в неподвижных обмотках и соответствуют проекциям вектора тока на неподвижную систему фазных осей координат. Поэтому при трансвекторном управлении АД необходимы координатные преобразования.

В неподвижной системе координат продольная и поперечная составляющие определяют амплитуду и фазу тока статора АД по отношению к магнитному потоку совершенно аналогично тому, как активная и реактивная составляющие определяют эти параметры по отношению к напряжению. Если задать значение продольной составляющей , соответствующим требуемому магнитному потоку, а поперечной  – требуемому моменту на валу, то тем самым будет определен вектор тока статора в синхронной системе координат. После этого, в соответствии с выражениями (1.7), можно преобразовать синхронную систему координат  в неподвижную  и разложить вектор тока на фазные проекции, в результате чего образуются синусоидальные сигналы, соответствующие фазным токам которые нужно сформировать в обмотках статора, чтобы получить заданный электромагнитный момент.

Преобразование системы координат невозможно без информации о пространственном положении опорного вектора  в каждый момент времени. Эту информацию можно получить непосредственным измерением магнитного потока статора или рабочего потока с помощью датчиков, а затем вычислить , или вычислить его по мгновенным значениям фазных напряжений и токов статора.

Трансвекторное управление реализуется техническими устройствами с различными функциями и алгоритмами, но суть его при этом остается неизменной и в дальнейшем мы рассмотрим несколько таких вариантов.
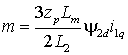