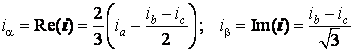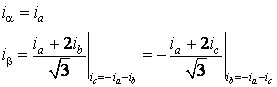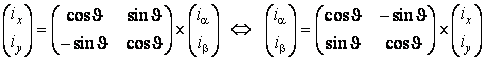1.1. Понятие обобщённого пространственного вектора

Современная теория электрических машин и электропривода строится на основе представления электромагнитных величин векторами. Это позволяет не только получить компактную запись уравнений, но также построить высокоэффективные системы управления, базирующиеся на векторных понятиях.

Большинство электрических машин переменного тока предназначено для работы в трехфазных сетях, поэтому они строятся с симметричными трехфазными обмотками на статоре, причем МДС этих обмоток распределены в пространстве по закону близкому к синусоидальному, т.е. МДС, создаваемая -й обмоткой в точке, отстоящей от оси этой обмотке на угол  равна –, где  – МДС, соответствующая оси -й обмотки.

Синусоидальность распределения позволяет представить МДС или пропорциональные им токи обобщённым пространственным вектором на плоскости, перпендикулярной оси ротора машины. В дальнейшем под обобщённым вектором будем понимать вектор, проекции которого на оси фазных обмоток в любой момент времени равны мгновенным значениям представляемых этим вектором фазных величин.

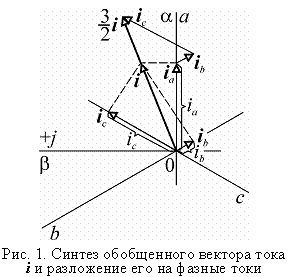Если ток в каждой обмотке представить вектором ( рис. 1), модуль которого равен мгновенному значению тока (), а направление совпадает с осью обмотки, и сложить эти векторы, то мы получим пространственный вектор тока . Модуль этого вектора будет в полтора раза больше модуля вектора , проекции которого на оси фазных обмоток равны мгновенным значениям фазных токов . Следовательно, для того, чтобы этот вектор соответствовал данному выше определению, его нужно уменьшить в полтора раза, умножив на коэффициент 2/3. В общем случае -фазной системы обмоток модуль суммарного вектора в -раз больше модуля обобщённого вектора и, соответственно, коэффициент, на который нужно умножать результат суммирования равен .

Для упрощения математических операций координаты точек любой плоскости можно объединить в комплексные числа. Тогда, совместив вещественную ось плоскости обобщённых векторов с осью обмотки фазы , можно записать описанные выше операции построения обобщённого вектора тока в виде

                              (1)

где 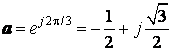 – оператор трёхфазной системы,  – векторы фазных токов, а  – мгновенные значения токов соответствующих обмоток. Обозначение вектора строчным символом принято для указания на то, что его координаты являются функциями времени аналогично тому, как строчные символы при обозначении скалярных величин указывают на мгновенное значение.

Основное свойство симметрии фазных величин заключается в равенстве нулю суммы фазных операторов. Для трехфазной системы это очевидно из равенства – .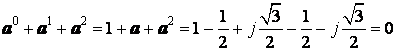

При симметричном питании фазные токи равны

.

Подставляя эти значения в (1), мы получим годограф вектора тока

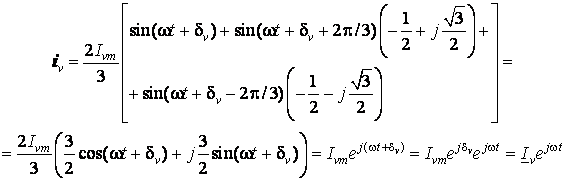  (2)

где  – временной вектор. Следовательно, в этом случае конец вектор тока перемещается в пространстве по окружности с радиусом равным амплитуде фазного тока  с угловой частотой . При этом в начальный момент времени () его угол с осью обмотки фазы  составляет .

При изменении порядка следования фаз токов их мгновенные значения будут определяться функциями

,

и обобщённый вектор тока будет равен

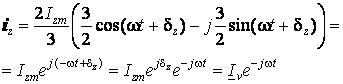,                  (3)

т.е. он будет описывать на плоскости окружность радиусом , вращаясь при этом в отрицательном направлении.

Из курса электротехники известно, что любую несимметричную трехфазную систему питания можно представить суммой трех симметричных составляющих: прямой, обратной и нулевой последовательности

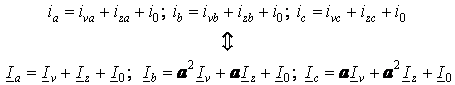,              (4)

значения которых через временные векторы или комплексные амплитуды фазных токов определяются как

. (5)

Подставляя фазные токи (4) в (1), мы получим с учетом (2) и (3) пространственный вектор тока

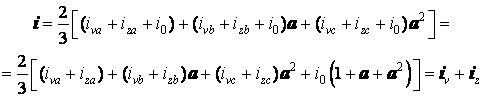
Это означает, что обобщённый вектор тока не содержит нулевой составляющей и ее при анализе нужно учитывать особо. Иными словами, при любом виде асимметрии обобщённый вектор будет содержать только симметричные составляющие прямой и обратной последовательности, т.е. .

Пусть начальные фазы обеих составляющих равны нулю (), тогда

.

Это выражение представляет собой параметрическое уравнение эллипса с полуосями, равными сумме и разности модулей составляющих прямой и обратной последовательности. При ненулевых начальных фазах в некоторый момент времени вектор тока займет положение, соответствующее большой оси эллипса. При этом должно выполняться условие  или . Значит, большая ось эллипса годографа вектора тока будет располагаться на биссектрисе угла между начальными фазами, т.е. под углом  к оси обмотки фазы .

Таким образом, при несимметричных фазных токах годографом пространственного вектора является эллипс, соотношение осей которого определяется степенью асимметрии. Предельным состоянием этого годографа при отсутствии асимметрии будет окружность, а при равенстве составляющих прямой и обратной последовательности – отрезок прямой с длиной равной двойному значению их модуля.

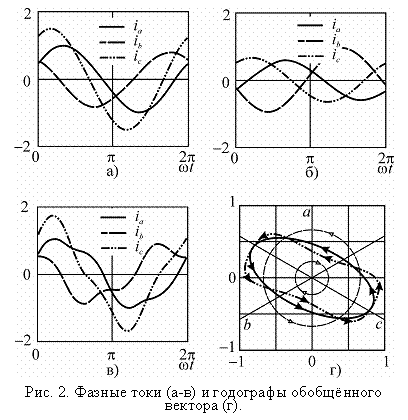
Рассмотрим в качестве примера случай некоторых произвольных фазных токов

,

показанных на рисунке 2 а). В соответствии с (5) симметричные составляющие этой системы равны

Следовательно, годографом вектора тока будет эллипс с большой и малой полуосями  и наклоном большой оси . Он показан на рис. 2 г) вместе с годографами симметричных составляющих (штриховые линии).

Если теперь выполнить суммирование , а затем определить проекции результирующего вектора на фазные оси (см. ниже), то мы получим новые функции фазных токов

показанные на рис. 2 б). Эти токи не содержат нулевой составляющей, поэтому существенно отличаются от исходных.

Для несинусоидальных величин также можно построить годограф обобщённого вектора. Пусть, например, рассмотренные выше несимметричные токи содержат еще и третью гармонику

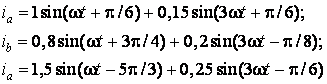
(рис. 2. в). Подставляя эти значения в (1) для интервала углов , мы получим координаты вектора  и построим его годограф. Он показан на рис. 2 г) штрих-пунктирной линией. Проводя касательные к этому годографу перпендикулярно фазным осям, можно и в этом случае убедиться, что амплитудные значения фазных токов, полученные из обобщённого вектора, существенно отличаются от исходных.

Обобщённый вектор, как и любой вектор на плоскости, можно представить через координаты точки его конца или, что то же самое, через его проекции на оси координат, алгебраической формой записи комплексного числа. Если оси вещественных и мнимых составляющих обозначить, как  и (рис. 1), то обобщённый вектор тока будет равен

.

Подставляя в выражение (1) значения оператора системы, записанные в алгебраической форме, и разделяя вещественную и мнимую части, получим

Переход от представления обобщённого вектора проекциями на оси фазных обмоток к представлению его проекциями на ортогональные оси комплексной плоскости эквивалентно преобразованию трехфазной системы обмоток в двухфазную. В матричной форме эти преобразования координат с учетом  можно записать в виде

При отсутствии нулевого провода . Тогда для определения проекций на оси  достаточно использовать два фазных тока, т.к.

                              (6)

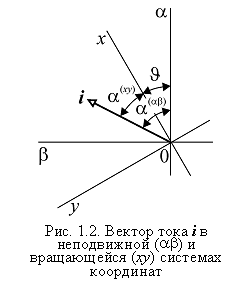
Пользуясь известными геометрическими понятиями, обобщённый вектор можно представить также во вращающейся системе координат. Если вектор тока представлен в неподвижной системе координат , то переход к новой системе координат , развернутой относительно исходной на некоторый угол  (рис. 2), осуществляется из очевидного соотношения аргументов комплексных чисел в виде

При этом следует заметить, что на угол  не накладывается никаких ограничений, т.е. он может иметь постоянное значение, но может также изменяться произвольным образом. Для системы координат вращающейся с угловой частотой  он равен – . Таким образом, если под  понимать оператор вращения, то переход к неподвижной системе координат  осуществляется умножением на оператор прямого вращения , а к вращающейся  – умножением на оператор обратного вращения

В развернутом виде преобразование координат  можно записать как

.

Отсюда можно представить связь между составляющими обобщённого вектора тока в различным системах координат в виде

           (7)

Преобразование системы координат является одной из важнейшей функций, используемых в современных системах управления приводом, которая позволяет изменить характер фазных величин. Пусть, например, рассматриваемая нами система токов содержит только составляющую прямой последовательности с частотой , т.е. фазные токи симметричны и . Тогда умножением на оператор вращения  вектор тока можно представить в синхронно вращающейся системе координат

.

В результате в синхронной системе координат фазные токи или проекции на координатные оси будут постоянными величинами

.

Если же синхронную систему координат сориентировать по вектору тока, т.е. использовать оператор вращения , то проекция  будет равна нулю, а -проекция станет равной модулю вектора .

С помощью обратных преобразований можно синтезировать вектор с заданными параметрами, т.е. модулем, начальной фазой и частотой вращения. Для этого нужно задать значения  и  проекций, а затем преобразовать их в неподвижную систему координат в соответствии с (1.7), где . При этом постоянные величины  и  в новой системе координат станут синусоидальными функциями времени с амплитудой , частотой  и начальной фазой  – .

При асимметрии фазных токов переход к прямо вращающейся системе координат даст нам проекции

т.е. фазные проекции будут содержать помимо постоянных значений, соответствующих составляющей тока прямой последовательности, также и синусоидальные функции времени с двойной частотой, соответствующие составляющей обратной последовательности.

Обобщёнными векторами можно представить также ЭДС , напряжения  и потокосцепления , при этом все свойства рассмотренного выше обобщённого вектора тока будут присущи и этим векторам