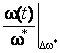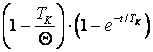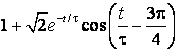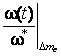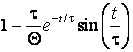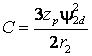Приложение 1.

Основное свойство симметричных m-фазных систем

В симметричной -фазной системе сумма мгновенных значений фазных величин равна нулю. Это свойство симметрии находит свое отражение в равенстве нулю суммы всех фазных операторов, т.е.

,

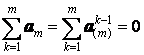где:  – оператор -й фазы;  – оператор системы, а  – целое число, определяющее порядок следования фаз.

В этом можно убедиться следующим образом. Запишем сумму фазных операторов в виде , полагая , т.к. для суммирования порядок следования фаз безразличен. Затем умножим обе части равенства на  и, преобразовав результат с учетом того, что , получим

.

Так как , то это равенство возможно только при условии .

Приложение 2.

Обобщённый вектор в симметричной m–фазной системе

Обобщённым называется вектор, проекции которого на оси фазных обмоток в любой момент времени равны мгновенному значению соответствующих фазных величин. Его можно построить суммированием векторов, направление которых совпадает с осями фазных обмоток, а модули равны мгновенным значениям. Назовем эти векторы – фазными. Аналитически операцию суммирования фазных векторов (например, векторов тока) можно представить в виде

где:  – мгновенное значение тока в -й фазе;  – оператор -й фазы;  – оператор симметричной системы фазных токов.

Пусть для произвольного момента времени задан обобщённый вектор тока , где  – угол между вектором  и вещественной осью. Тогда по определению фазные токи и фазные векторы равны

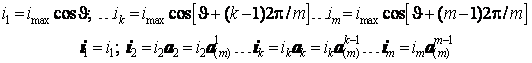
Отсюда вектор, полученный геометрическим суммированием фазных токов, будет равен

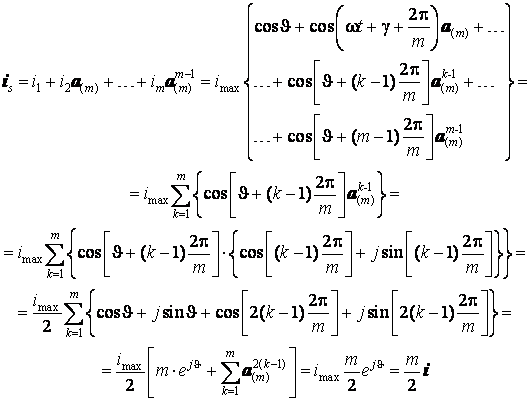   (п.2.1)

Последнее преобразование суммы справедливо потому, что множитель 2 в показателе степени фазного оператора определяет порядок следования фаз и не влияет на результат суммирования, т.е. 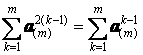, а из основного свойства симметричных систем (см. приложение 1) следует, что .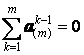

Таким образом, вектор , полученный в результате суммирования, превосходит по модулю обобщённый вектор  в  раз, поэтому в -фазной системе для получения обобщённого вектора результат суммирования нужно умножить на коэффициент , т.е. .

Из выражений (п.2.1) следует, что

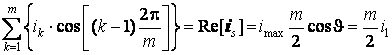.                                 (п.2.2.)

Приложение 3.

Индексы систем координат принятые в пособии

Индекс системы	Частота вращения	Ориентация вещественной оси	Название  системы
	0	по оси обмотки фазы  статора	неподвижная
		по оси обмотки фазы  ротора	синхронная с ротором
		произвольная	синхронная с магнитным полем
		по вектору потокосцепления  ротора	синхронная с магнитным полем
	произв.	произвольная	произвольная

Приложение 4.

Передаточные функции и переходные характеристики при различных настройках регулятора скорости в трансвекторной системе

Функции	Тип регулятора
	П	ПИ
;  ;   ;