2.1.1 Влияние частоты питания на электромагнитные процессы в АД.

Изучение влияния изменения частоты питания начнем с электромагнитных процессов в АД. Для этого запишем векторное уравнение цепи статора обобщенной электрической машины в неподвижной системе координат (), опуская индекс системы:

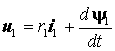                                                                   (1)

Далее представим полное потокосцепление статора в виде суммы потокосцепления рассеяния и основного потокосцепления . Потокосцепление рассеяния создается током статора и его можно представить как . Подставляя эти выражения в (1), получим

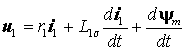.                                                 (2)

Уравнение (2) не содержит ЭДС вращения, поэтому уравнения фазных напряжений будут иметь точно такой же вид. В символической форме уравнение фазного напряжения можно записать в виде

.                             (3)

Здесь потокосцепление  представлено через эффективное число витков обмотки статора  и комплексную амплитуду основного магнитного потока , а множители  соответствуют операции дифференцирования в уравнении (2). Отсюда комплексная амплитуда потока

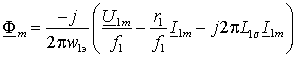.                     (4)

Если принять , то амплитуда основного магнитного потока будет равна 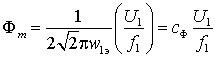, т.е. будет определяться соотношением , которое в данном случае будет выполнять функцию аналогичную току возбуждения машины постоянного тока. Поэтому для поддержания постоянного основного магнитного потока при изменении частоты питания АД необходимо одновременно изменять напряжение питания.

Активное сопротивление обмотки статора  обычно относительно невелико, но все же имеет конечную величину. Поэтому второе слагаемое в (4) при уменьшении частоты увеличивается, снижая основной поток АД. Это снижение пропорционально также величине тока статора и увеличивается по мере увеличения нагрузки АД. Его можно компенсировать соответствующим увеличением напряжения , однако, при любом конечном значении  и  существует такое значение частоты питания , при котором поток снижается до нуля.

Третье слагаемое в уравнении (4) также по мере роста нагрузки снижает магнитный поток. Но, в отличие от второго, это снижение не зависит от частоты и определяется только током статора.

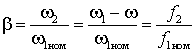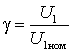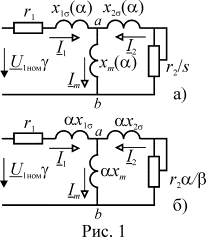
Введем относительные величины: частоту статора , частоту ротора  и напряжение статора . Тогда уравнения цепей статора и ротора, а также схему замещения АД в статическом режиме можно представить так, как показано на рис. 1 а,

где –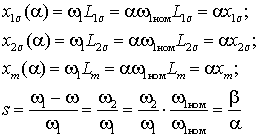

Используя эти выражения, преобразуем схему замещения к виду рис. 1 б, где все параметры соответствуют номинальной частоте питания.

Эта схема наглядно иллюстрирует рассмотренные выше изменения основного магнитного потока при изменении частоты. При уменьшении частоты все сопротивления схемы замещения, кроме , будут уменьшаться и входное напряжение перераспределяться между  и всей остальной частью цепи так, что  и .

Нетрудно заметить, что относительная частота ротора  в схеме замещения рис. 1 играет такую же роль, как относительное скольжение  при постоянной частоте. При переменной частоте скольжение  не может служить параметром однозначно определяющим режим двигателя, т.к. оно зависит от частоты () и в теории частотного управления относительная частота ротора  называется абсолютным скольжением.

Пользуясь схемой замещения рис. 1, можно определить зависимости всех величин (, , ,  и ) от регулируемых параметров .

Таблица 1

Величина	Значение при независимом напряжении	Значение при независимом магнитном потоке	Значение при независимом токе статора
		*
			*

В таблице 1 приняты следующие обозначения:

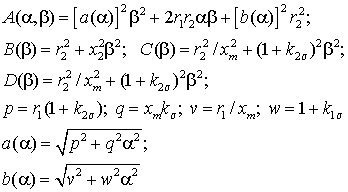
где  – конструктивная постоянная статора; – число витков и обмоточный коэффициент статора;  – коэффициенты рассеяния статора, ротора и общий;  – относительное значение магнитного потока в зазоре.

Преобразуем выражение для момента АД при независимом управлении напряжением, разделив числитель и знаменатель на , тогда

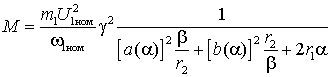.         (5)

Выражение (5) можно представить в форме Клосса

,                                            (6)

где: 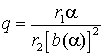;  – критическое абсолютное скольжение; 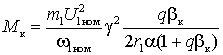 – критический момент.

Критическое скольжение  зависит только от частоты статора , а критический момент – также и от напряжения , причем, эта зависимость очень сильная (квадратичная).

Жесткость механической характеристики можно оценить касательной в точке холостого хода

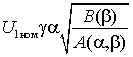
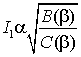
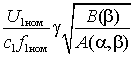
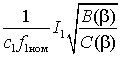
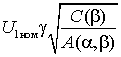
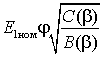
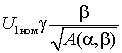
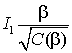
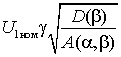
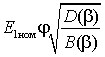
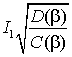
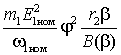
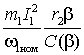
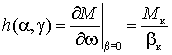.                                        (7)