1.2.4.3 Электромагнитный момент

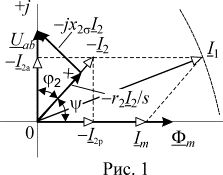
Определим электромагнитный момент АДУТ, воспользовавшись векторным представлением токов

,

где  – число фаз статора;  – число пар полюсов;  и  – пространственные векторы токов ротора и намагничивания;   и  – их модули или амплитуды соответствующих токов, а  – угол между векторами (рис. 1). Но . Учитывая это равенство и переходя к действующим значениям, получим

,

где  – активная составляющая тока ротора. Найти эту составляющую несложно, пользуясь схемой замещения и законом Ома в символической форме –

,

Тогда, с учетом , электромагнитный момент АД будет равен –

,                                                                 (1)

где 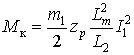 – критический момент,  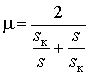– относительное значение момента, а  – критическое скольжение.

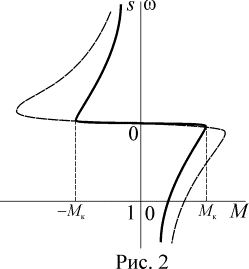
Нетрудно заметить, что выражение (1) представляет собой формулу Клосса, но в отличие от режима питания источником ЭДС, в ней отсутствуют элементы . Это вполне объяснимо, т.к. питание от источника тока исключает влияние на процессы в АД падения напряжения в цепи статора () и в этом смысле эквивалентно условию . Как следствие этого, критические моменты при токовом питании в двигательном и генераторном режимах одинаковы (сплошная линия на рис. 2) и вся механическая характеристика симметрична относительно точки холостого хода. Сравнивая критические моменты в двигательном режиме при двух видах питания и полагая, что ток статора равен номинальному, получим для их отношения

.

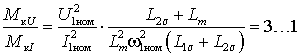Сопоставляя аналогично критические скольжения, получим

.

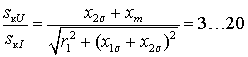При питании от источника тока АД развивает при прочих равных условиях больший электромагнитный момент, чем в случае питания от источника ЭДС. Для получения представления о количественном соотношении положим  и сопоставим критический момент с моментом , соответствующим номинальному скольжению при питании от источника ЭДС. Тогда для двигателей мощностью от 1 до 90 кВт получим

.

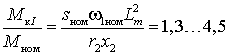На самом деле это отношение будет большим, т.к. номинальный момент здесь рассчитывается по значению тока ротора при условии приближенного равенства , в то время как . Способность АД развивать больший момент при питании от источника тока широко используется для разгона гиродвигателей.

Проанализируем влияние частоты источника питания. Для этого введём традиционные для теории частотного управления параметры, обозначив относительные частоты статора и ротора как  и , где  и  – действительные частоты, а  – номинальная частота тока статора АД. Тогда текущее и критическое скольжения можно представить в виде  и , полагая абсолютное критическое скольжение  равным критическому скольжению при номинальной частоте.

Подставив полученные выражения в уравнение механической характеристики (1), получим частотно независимое выражение

,

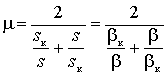а т.к. критический момент также не зависит от частоты, то механические характеристики при изменении частоты 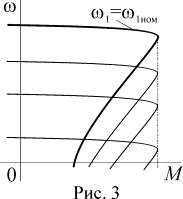будут просто смещаться параллельно естественной характеристике (рис. 3), сохраняя значения максимального момента и критического скольжения. Поэтому диапазон регулирования скорости вращения АД при питании от источника тока

,

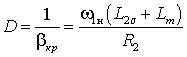будет существенно больше, чем при питании от источника ЭДС. В реальной машине этот диапазон будет несколько меньше, т.к. в ней сказывается влияние насыщения магнитопровода (уменьшение ) и нагрева обмотки ротора (увеличение ).