1.2.4.1 Круговая диаграмма АД при питании от источника тока

В последнее время в связи с развитие регулируемого асинхронного электропривода возникла необходимость изучения свойств АД при питании его от источника тока. Это объясняется тем, что значительная часть преобразователей частоты используемых в приводе обладает свойствами источника тока, т.к. формируют в фазах двигателя токи, не зависящие от режима работы машины и ее параметров.

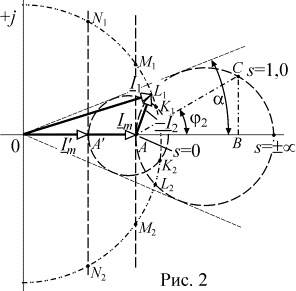
В этом случае схема замещения АД имеет вид, показанный на рис. 1. Построим векторную диаграмму этой цепи, совместив, как обычно, вектор основного магнитного потока Ф_m с вещественной осью (рис. 2). Тогда ток намагничивания  будет сонаправлен с потоком.

Напряжение  в ветви ротора уравновешивается суммой падений напряжений на  и  и при изменении скольжения вектор тока ротора  описывает окружность диаметром  с центром, расположенным в точке , где  – коэффициент рассеяния ротора.

Поскольку в исследуемой модели мы пренебрегаем потерями в магнитопроводе, то все точки, отделяющие на круговой диаграмме дуги, соответствующие режимам работы АД, будут симметричными относительно вещественной оси. Точки холостого хода () и бесконечно больших скольжений () расположатся на вещественной оси, а точка короткого замыкания () – на пересечении гипотенузы (или её продолжения) прямоугольного треугольника ABC, катетами которого в некотором масштабе являются  (AB) и  (BC).

Так как в АДУТ значение тока статора остаётся неизменным во всех режимах, то геометрическим местом точек конца вектора  является дуга окружности  с центром в начале координат и радиусом равным .

С другой стороны, ток  получается суммированием тока намагничивания и тока ротора, поэтому конец этого вектора должен располагаться в точке круговой диаграммы тока , соответствующей режиму работы АД (скольжению ). Следовательно, он будет располагаться в точке пересечения дуги окружности, соответствующей его модулю, с окружностью круговой диаграммы тока .

Изменение режима работы АД будет приводить к изменению полного сопротивления участка схемы замещения, что, при постоянном значении , вызовет изменение падения напряжения . С напряжением  линейно связаны ток намагничивания и диаметр окружности круговой диаграммы. Поэтому при изменении режима работы АД круговая диаграмма будет изменять диаметр и положение центра, оставаясь внутри касательных, образующих с вещественной осью угол 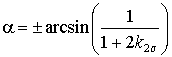. Это непосредственно следует из рассмотрения прямоугольного треугольника, гипотенузой которого является центр круговой диаграммы , а катетами – радиус круговой диаграммы 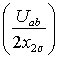 и касательная к ней, проведённая из начала координат. Отсюда –

На рис. 2 показаны два режима работы АД и соответствующие этим режимам круговые диаграммы. Чтобы не усложнять рисунок, векторы токов изображены только для одного из режимов. В первом случае вектор  находится в точке , расположенной на дуге двигательного режима АД. При увеличении скольжения двигатель переходит в режим торможения. Вследствие уменьшения  диаметр круговой диаграммы уменьшается, и она смещается к началу координат вдоль касательных, образуя новую точку конца вектора – . Точки и  соответствуют таким же скольжениям в генераторном режиме. Предельными положениями круговой диаграммы будут касания дуги тока снаружи (режим холостого хода) и внутри (режим бесконечно большого скольжения).

Существенным параметром, определяющим интенсивность трансформации векторной диаграммы токов, является коэффициент рассеяния ротора . В частности, он определяет величину дуги полуокружности тока , в пределах которой может находиться ток статора при всех возможных режимах работы АД (угол ).

Если пренебречь потоком рассеяния ротора, то окружности векторных диаграмм выродятся в прямые линии  и , проходящие через точки концов векторов тока намагничивания (рис. 2). При этом ток  потеряет реактивную составляющую.