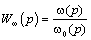.
Для анализа свойств электропривода с линейной механической характеристикой как объекта автоматического управления найдем передаточную функцию системы по управляющему воздействию:
.
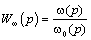Из рис. 7.1 можно записать:
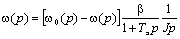
или
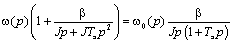
или
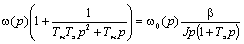
или
.
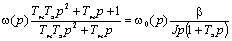Отсюда
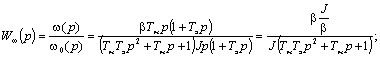
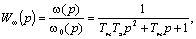(7.4)
где
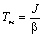(7.5) – электромеханическая
постоянная времени.
Передаточная функция по возмущающему воздействию - моменту статической нагрузки МС, имеет вид:
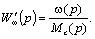
Из рис. 7.1 получаем:
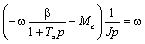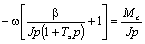или
или
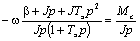, отсюда
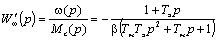(7.5)
Характеристическое уравнение системы:
.
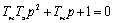Корни этого уравнения:
,
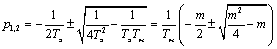где
.
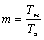Значение m определяет колебательность разомкнутой электромеханической системы.
Если m > 4, то p1= -α1; p2 = -α2.
Поэтому в этом случае:
; 
; 
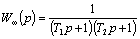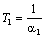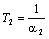(7.6)
Следовательно, при m > 4 рассматриваемый электропривод может быть представлен в виде последовательного соединения инерционных звеньев с постоянными времени Т1 и Т2.
При m = 4 характеристическое уравнение системы имеет два равных
отрицательных корня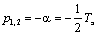 
. В этом случае:
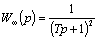(7.7)
где
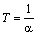
При m<4
характеристическое уравнение имеет комплексно-сопряженные корни
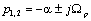и электропривод
представляет собой колебательное звено с коэффициентом затухания ξ меньшим или равным 1, уменьшающимся по мере уменьшения m.
В этом случае можно записать:
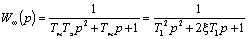(7.8)
; 
;
.
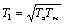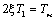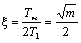Анализ частотных характеристик двигателей мощностью выше 10кВт показал, что передаточную функцию по управляющему воздействию можно представить в виде:
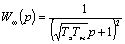(7.9)
т.е. заменить колебательное звено двумя апериодическими с постоянной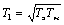 
.
Для многих электроприводов малой мощности m>4, при этом можно пренебречь электромагнитной инерцией, положив Тэ»0, тогда структурная схема асинхронного электропривода с линеаризованной механической характеристикой будет иметь вид (рис. 7.3):
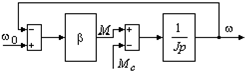
Рис. 7.3. Структурная
схема асинхронного электропривода с линеаризованной механической
характеристикой и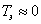 
.
Из рис. 7.3 после элементарных преобразований:
;
;
;
;
;
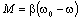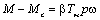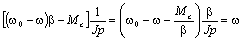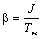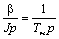
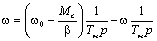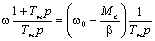
получаем:
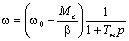(7.10.)
Полученное уравнение позволяет структурную схему асинхронной машины с линеаризованной механической характеристикой представить в виде (рис. 7.4):
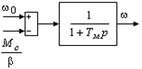
Рис. 7.4. Преобразованная структурная схема асинхронной машины с линеаризованной механической характеристикой.
Из преобразованной структурной схемы видно, что при Тэ»0 электропривод с линейной механической характеристикой приближенно можно представить в виде инерционного звена с постоянной времени Тм.
Переходную и весовую функции инерционного звена можно представить в виде:
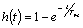(7.11)
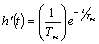(7.12)
По уравнениям
(7.11) и (7.12) на рис. 7.5 построены временные характеристики электропривода при .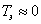
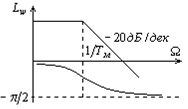
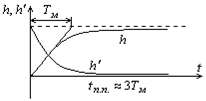
а) б)
Рис.7.5. Временные характеристики электропривода при .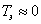
Из полученных временных характеристик можно сделать вывод: электромеханическая постоянная времени Тм представляет собой время, за которое электропривод достиг бы установившейся скорости, двигаясь равномерно ускоренно под действием постоянного динамического момента, равного начальному значению:
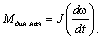(7.13)