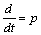
Для анализа динамических
характеристик машины постоянного тока в системе уравнений, описывающих
механические характеристики двигателя, произведем подстановку: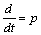
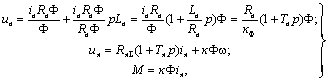(6.13)
где
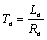- электромагнитная постоянная времени обмотки возбуждения;
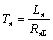- электромагнитная постоянная времени цепи якоря;
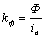- коэффициент, соответствующий линейной части кривой
намагничивания двигателя.
Структурная схема электромеханического преобразования энергии, соответствующая полученной системе уравнений:
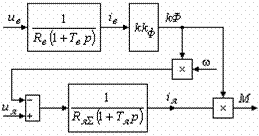
Рис. 6.2. Структурная схема электромеханического преобразователя энергии с независимым возбуждением и с двумя каналами управления: полем двигателя и напряжением якоря.
Из схемы видно, что при отсутствии реакции якоря на величину потока возбуждения, процессы в цепи возбуждения происходят независимо от процессов в цепи якоря. В то же время процессы изменения тока якоря и момента машины зависят от изменения магнитного потока.
При отсутствии добавочных резисторов в цепи возбуждения постоянная времени цепи возбуждения лежит в пределах (0,2..5)с, причем с увеличением мощности она возрастает.
Изменение магнитного потока приводит к нелинейности в третьем уравнении системы, описывающей электромеханическое преобразование энергии, даже при ненасыщенной магнитной цепи, поэтому при управлении по цепи возбуждения для анализа динамических свойств электропривода используются ЭВМ.
Рассмотрим случай питания двигателя постоянного тока с независимым возбуждением от источника напряжения. При этом Φ=const и уравнение механической характеристики двигателя можно получить из уравнения:
,
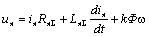отсюда:
;
;
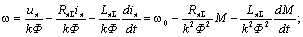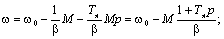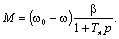(6.14)
Следовательно, динамические свойства электромеханического преобразователя с независимым возбуждением описываются структурной схемой:
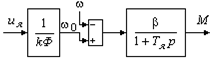
Рис. 6.3. Структурная схема электромеханического преобразователя энергии с управлением напряжением якоря.
Постоянная якорной цепи двигателя средней и большой мощности лежит в пределах Тя=(0,02..0,1)с, причем наибольшие значения соответствуют некомпенсированным или тихоходным двигателям большой мощности.
Динамическая характеристика двигателя постоянного тока зависит от характеристики механической части, начальных условий, уровня и характера возмущающих воздействий. Если нагрузка электродвигателя имеет пульсирующий характер:
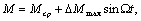(6.15)
то закон изменения скорости определим, выполнив преобразования:
.
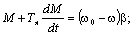
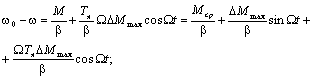
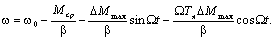Из
последнего уравнения (6.12) имеем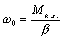 
.
Подставив выражение для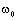 
в уравнение для
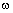, получим:
;
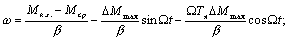
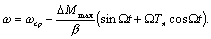
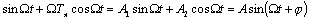
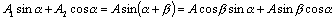
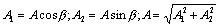
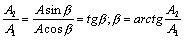
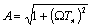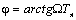
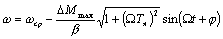(6.16)
По уравнению (6.16) на рис. 6.4 показана динамическая механическая характеристика двигателя с независимым возбуждением в режиме установившихся колебаний.
Динамическая характеристика (эллипс 1) отличается от статической характеристики (прямая 2). Отличие объясняется влиянием на вид динамической характеристики электромагнитной инерции якорной цепи, выраженной постоянной Тя. Уменьшение частоты вынужденных колебаний Ω или снижение постоянной времени Тя приводит к снижению отклонений динамических характеристик от статических, и в пределе при Тя или Ω, стремящихся к 0, динамическая характеристика сливается со статической.
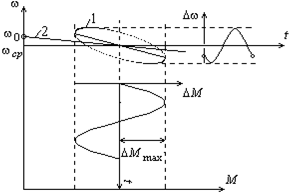
Рис. 6.4. Динамическая механическая характеристика двигателя с независимым возбуждением в режиме установившихся колебаний.
Используя структурную схему электромеханического преобразователя, определим передаточную функцию динамической жесткости механической характеристики:
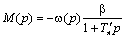
Из этого выражения получаем:
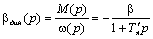(6.17)
Амплитудно-фазовую характеристику динамической жесткости получим подстановкой в полученное уравнение р=jΩ:
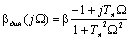(6.18)
Выражения для АЧХ и ФЧХ динамической жесткости:
;
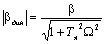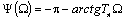(6.19)
Из амплитудно-фазовых характеристик (рис. 5.5) видно, что с увеличением частоты вынужденных колебаний Ω модуль динамической жесткости уменьшается. Сдвиг по фазе между кривыми колебания скорости и момента изменяется от значения -180°, соответствующего статической жесткости (Ω=0), до -270°при Ω, стремящемся к бесконечности;. Введение добавочных резисторов в цепь якоря уменьшает Тя и, если с увеличением частоты, величины модуля и фазы динамической жесткости изменяются незначительно, то можно без существенных погрешностей исследовать динамические процессы, пользуясь выражением для статической жесткости.
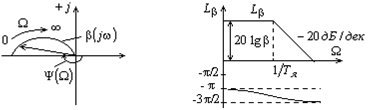
а) б)
Рис. 6.5. Частотные характеристики динамической жесткости двигателя с независимым возбуждением.
У двигателя постоянного тока с независимым возбуждением величина Тя относительно мала, поэтому они имеют высокие динамические характеристики. Сказанное справедливо лишь для двигателя с компенсационной обмоткой. При отсутствии последней вследствие реакции якоря величина потока машины может уменьшаться на величину, достигающую 20%. Изменения потока происходят с постоянной времени цепи возбуждения Тв, которая значительно выше Тя. Поэтому при проявлениях реакции якоря расхождения между статическими и динамическими характеристиками у двигателей без КО проявляются при меньших частотах.
При питании машины постоянного тока от источника тока, уравнения механической и электромеханической характеристик примут вид:
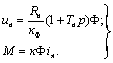(6.20)
После несложных преобразований имеем:
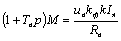
Структурная схема машины постоянного тока при питании ее от источника тока имеет вид (рис. 6.6):
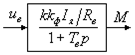
Рис. 6.6. Структурная схема электромеханического преобразователя постоянного тока при питании от источника тока.
Отсутствие зависимости тока якоря от скорости исключает проявление электромеханической связи, поэтому жесткость статической механической характеристики двигателя М=f(ω) при Uв=const равна нулю.
Как объект САУ, электромеханический преобразователь представляет собой апериодическое звено первого порядка с большой постоянной времени; управляющим воздействием является напряжение возбуждения. Электромеханический преобразователь является источником момента М=const, значение которого можно изменять, управляя величиной тока возбуждения.