5.3. Динамические свойства синхронного двигателя
При идеальном холстом ходе I1q=0 и вектор 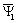 (рис. 5.1в) совпадает с осью d (Θэл=0).
Под нагрузкой ось ротора d и составляющая Ψ1 d , которая в основном определяется током возбуждения I в , отстают от оси вращающегося магнитного поля на угол Θэл.
Между постоянным магнитом, которым является возбужденный ротор, и вращающимся
магнитным полем возникают силы взаимодействия. При малых углах Θэл
эти силы изменяются по линейному закону. Это электромагнитное взаимодействие
подобно механической упругой связи между полем ротора
и результирующим полем машины. Поэтому по своим динамическим свойствам
синхронный двигатель подобен упругим механическим системам.
(рис. 5.1в) совпадает с осью d (Θэл=0).
Под нагрузкой ось ротора d и составляющая Ψ1 d , которая в основном определяется током возбуждения I в , отстают от оси вращающегося магнитного поля на угол Θэл.
Между постоянным магнитом, которым является возбужденный ротор, и вращающимся
магнитным полем возникают силы взаимодействия. При малых углах Θэл
эти силы изменяются по линейному закону. Это электромагнитное взаимодействие
подобно механической упругой связи между полем ротора
и результирующим полем машины. Поэтому по своим динамическим свойствам
синхронный двигатель подобен упругим механическим системам.
Рабочий
участок угловой характеристики M=f(Θэл)
можно с достаточной точностью для многих задач инженерной практики заменить
линейной зависимостью M=kΘэл,
проходящей через точку номинального режима:
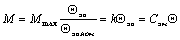 (5.11)
(5.11)
где
Cэм – коэффициент жесткости упругой
электромагнитной связи двигателя.
Продифференцировав выражение (5.11), получим:
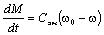 (5.12)
(5.12)
Аналогия между
электромагнитными взаимодействиями в синхронном двигателе и механической
пружине поясняет повышенную склонность синхронного двигателя к колебаниям. Для снижения
этой склонности реальные синхронные двигатели снабжаются демпферной или пусковой короткозамкнутой обмоткой, которая создает
асинхронный момент.
Результирующий
момент в асинхронной машине можно приближенно считать равным сумме синхронного Мсин и
асинхронного Мас
моментов:
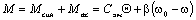 (5.13)
(5.13)
где
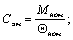 ;
;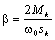 .
.
Уравнение
механической характеристики с учетом пренебрежения влиянием электромагнитной
инерции на асинхронный момент будет иметь вид:
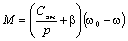 (5.14)
(5.14)
(Из выражения (5.12)
имеем
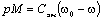 ;
;
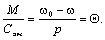
Подставив 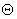 в выражение (5.13),
окончательно получим (5.14).)
в выражение (5.13),
окончательно получим (5.14).)
Структурная
схема электромеханического преобразователя, соответствующая этому уравнению
(рис. 5.3a):
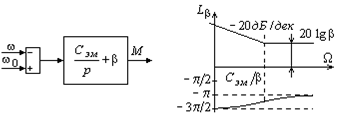
Рис.
5.3. Передаточная функция динамической жесткости синхронного двигателя (а) и
его ЛАЧХ (б).
При р=0 получаем
уравнение статической механической характеристики ω=ω0=const. В статическом
режиме изменения нагрузки на валу двигателя не приводят к изменениям скорости,
т.к. модуль статической жесткости равен бесконечности. При значениях нагрузки,
превышающих Mmax=λMном, двигатель выпадает из
синхронизма. Статическая механическая характеристика синхронного двигателя
имеет вид прямой 1 (рис. 5.4).
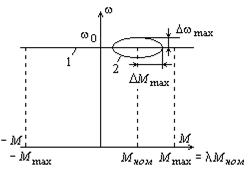
Рис.
5.4. Механические характеристики синхронного двигателя.
В динамических режимах механическая характеристика синхронного
двигателя не является абсолютно жесткой. В режиме установившихся колебаний
динамическая механическая характеристика имеет вид эллипса (кривая 2, рис.
5.4).
Передаточная
функция динамической жесткости определяется выражением:
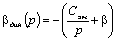 (5.15)
(5.15)
Следовательно АЧХ и ФЧХ динамической жесткости определяются
выражениями:
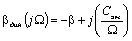 ;
;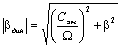 (5.16)
(5.16)
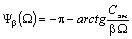 (5.17)
(5.17)
Используя
выражения (5.16) и (5.17) на рис. 5.3б, построены АЧХ и ФЧХ динамической
жесткости асинхронного двигателя.
Динамические
механические характеристики, соответствующие даже сравнительно медленным
изменениям момента двигателя, могут существенно отличаться от статических.
Важным
достоинством синхронного двигателя является возможность регулирования
реактивной мощности посредством изменения величины тока возбуждения Iв. При относительно небольшом токе возбуждения ток
статора I1 отстает от
приложенного напряжения на угол φ1 и
из сети потребляется реактивная мощность. Увеличивая ток возбуждения можно
добиться φ1=0, что соответствует
потреблению из сети только активной мощности. Дальнейшее увеличение тока
возбуждения Iв приводит к отдаче
реактивной мощности в сеть (рис.5.1в).
Увеличение
тока возбуждения, а значит и ЭДС Е
приводит к увеличению момента машины, а при неизменном моменте - к уменьшению
угла Θэл.
Как следует из выражения для угловой характеристики синхронной машины,
увеличение тока возбуждения приводит к увеличению перегрузочной способности
синхронного двигателя. Поэтому форсирование возбуждения при бросках нагрузки
позволяет повысить устойчивость работы двигателя в этих режимах.
ОГЛАВЛЕНИЕ
 (рис. 5.1в) совпадает с осью d (Θэл=0).
Под нагрузкой ось ротора d и составляющая Ψ1 d , которая в основном определяется током возбуждения I в , отстают от оси вращающегося магнитного поля на угол Θэл.
Между постоянным магнитом, которым является возбужденный ротор, и вращающимся
магнитным полем возникают силы взаимодействия. При малых углах Θэл
эти силы изменяются по линейному закону. Это электромагнитное взаимодействие
подобно механической упругой связи между полем ротора
и результирующим полем машины. Поэтому по своим динамическим свойствам
синхронный двигатель подобен упругим механическим системам.
(рис. 5.1в) совпадает с осью d (Θэл=0).
Под нагрузкой ось ротора d и составляющая Ψ1 d , которая в основном определяется током возбуждения I в , отстают от оси вращающегося магнитного поля на угол Θэл.
Между постоянным магнитом, которым является возбужденный ротор, и вращающимся
магнитным полем возникают силы взаимодействия. При малых углах Θэл
эти силы изменяются по линейному закону. Это электромагнитное взаимодействие
подобно механической упругой связи между полем ротора
и результирующим полем машины. Поэтому по своим динамическим свойствам
синхронный двигатель подобен упругим механическим системам. 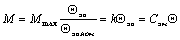 (5.11)
(5.11)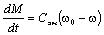 (5.12)
(5.12)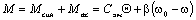 (5.13)
(5.13)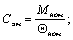 ;
;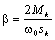 .
.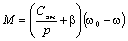 (5.14)
(5.14)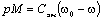 ;
;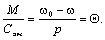
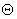 в выражение (5.13),
окончательно получим (5.14).)
в выражение (5.13),
окончательно получим (5.14).)

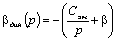 (5.15)
(5.15)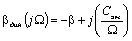 ;
;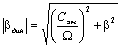 (5.16)
(5.16)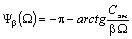 (5.17)
(5.17)