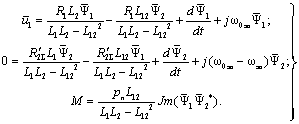
Как было показано ранее, при питании асинхронного двигателя от источника напряжения наиболее эффективные возможности управления обеспечиваются использованием в качестве управляющего воздействия в канале регулирования скорости частоты f, а в канале регулирования потока напряжения u.
Анализ динамических процессов преобразования энергии в асинхронном двигателе в виду сложности задачи, обусловленной нелинейностью уравнений, целесообразно вести с применением вычислительной техники.
Уравнения механической характеристики имеют вид:
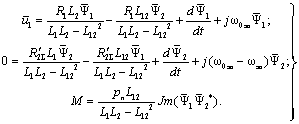
Каждое уравнение решим относительно производной потокосцепления:
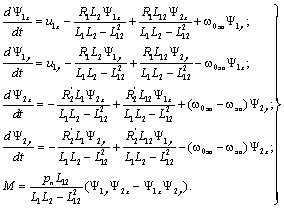(4.13)
Структурная схема электромеханического преобразования энергии в асинхронном электродвигателе при питании от источника напряжения изображена на рисунке 4.7.
Аналитическая оценка динамических свойств
асинхронного электромеханического преобразователя может быть получена для
режимов малых отклонений скорости от статического значения путем разложения
полученной системы в ряд Тейлора. Это правомочно для области рабочего участка
механической характеристики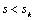 
в режимах, когда
магнитный поток машины изменяется незначительно. В этом случае предполагается,
что отклонения скорости от значения, определяемого статической характеристикой,
малы, а изменения токов не вызывают существенного изменения потокосцепления
статора Ψ1.
Для этих условий, положив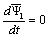 
, из уравнения (4.1) определим выражение для потокосцепления:
.
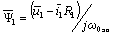При питании от источника напряжения и постоянстве
скорости вращения поля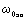 
изменения 
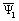вызываются лишь изменениями падения напряжения на активном
сопротивлении статора R1.
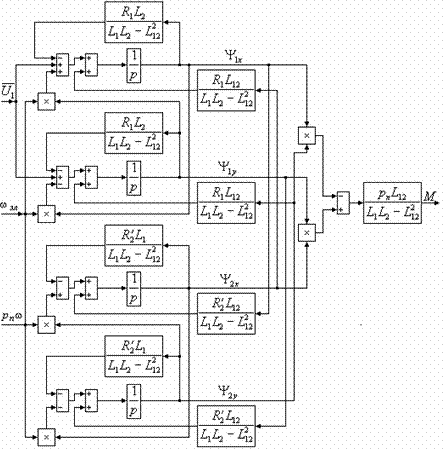
Рис. 4.7. Структурная схема электромеханического преобразованияэнергии в асинхронном двигателе.
Следовательно, при R1»0 для поддержания постоянства потокосцепления достаточно изменять напряжение питания пропорционально частоте:
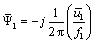(4.14)
т.е.
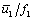не должно изменяться с
изменением частоты питания.
Пусть к обмоткам статора обобщенной машины
приложена система синусоидальных напряжений, которым соответствует вектор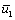 
, совпадающий по направлению с осью x, т.е. в
осях x, y:
u1x = u1max = const; u1y =0.
Тогда в соответствии с последним выражением:
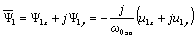
или
,
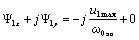отсюда:
; 
.
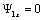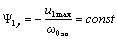Эти выражения можно получить, если подставить в первые два уравнения системы из пяти уравнений (4.13):
R1» 0; Ψ1x=0; Ψ1y=const; u1x = u1max = const; u1y = 0.
Выполним вспомогательные преобразования:
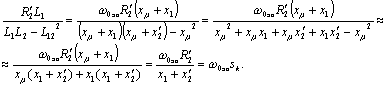
Здесь использовались следующие выражения:
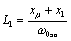
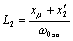
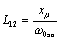(из схемы замещения);
;
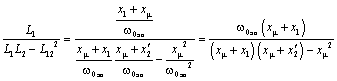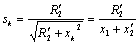при R 1 »0.
С учетом полученных соотношений, последние три уравнения системы, описывающей динамические свойства асинхронного двигателя, принимают следующий вид:
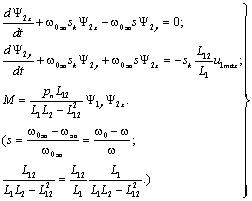(4.15)
Система нелинейна, т.к.
содержит произведения sΨ2x и sΨ2y. Однако в таком
виде, благодаря линейной зависимости момента от Ψ2x(Ψ1 y =const), можно путем
преобразований получить уравнение, непосредственно связывающее момент и
скольжение в динамических режимах. Положив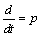 
, произведем преобразования уравнений системы, имея в виду,
однако, что эти уравнения нелинейны и поэтому
допустимы только такие их преобразования, при которых строго сохраняется
предусмотренный исходными уравнениями порядок дифференцирования переменных.
В начале из первого уравнения определим Ψ2 y :
.
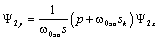Подставив полученное выражение для Ψ2 y во второе уравнение системы из трех уравнений (4.15), и соблюдая получающийся порядок дифференцирования переменных, получаем выражение для Ψ2 x :
.
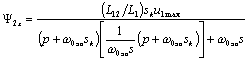Теперь подставив последнее выражение в третье уравнение системы (4.15), получим упрощенное уравнение динамической механической характеристики в виде:
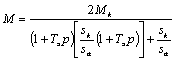(4.16)
здесь
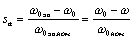(4.17)
–
абсолютное скольжение, равное отношению отклонения скорости двигателя ω от скорости поля ω0 при любой частоте f1 к скорости поля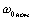 
при частоте f1ном;
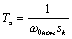(4.18)
электромагнитная постоянная времени;
.
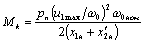С учетом выражения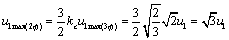 
, получаем:
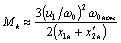(4.19)
Уравнение механической характеристики в статическом режиме работы, когда р=0, переходит в формулу Клосса:
.
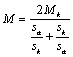Механические характеристики асинхронной машины, построенные по этой формуле, имеют вид (рис. 4.8):
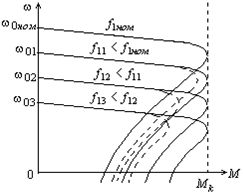
Рис. 4.8. Механические характеристики асинхронной машины.
Реально в выражении для механической характеристики величиной R1 можно пренебречь только при частотах, близких к номинальной и I1 меньше или равно 2Iн. При снижении частоты и пропорциональном снижении напряжения фазы u ф роль R1I1 непрерывно возрастает, что приводит к отличию расчетных кривых механической характеристики от реальных (пунктирные кривые на рисунке).
Продифференцируем выражение для М:
;
;
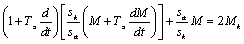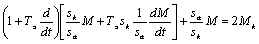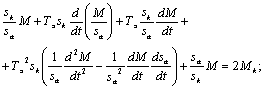
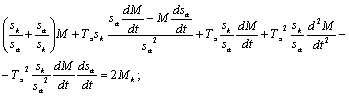
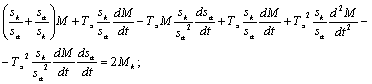
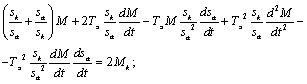
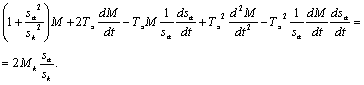
Раскладываем полученное уравнение в ряд Тейлора в окрестности точки M0, sa0.
(Пусть нелинейное дифференциальное уравнение имеет вид:
,
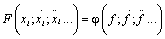где
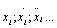- переменные системы и их производные по времени (i=1,2,3…);
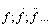- управляющие и возмущающие воздействия
и их производные по времени.
При линеаризации функция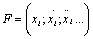 
раскладывается
в ряд по степеням отклонений переменных, причем производные рассматриваются как
самостоятельные переменные.
Линеаризованное уравнение (пренебрегают членами высшего порядка малости) имеет вид:
,
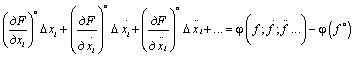где
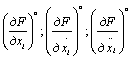– частные производные от F по соответствующим
переменным при значении переменных: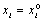 
, 
, 
.
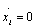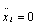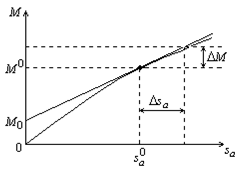
Рис. 4.9. К линеаризации механической характеристики асинхронной машины.
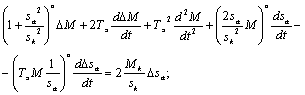
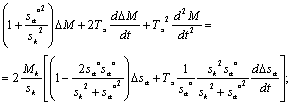
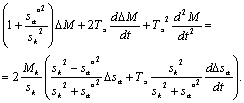
Положив в полученном выражении:
, 
, 
, 
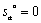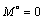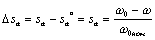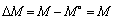, получим
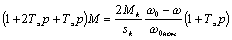
или, окончательно
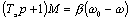(4.20)
где
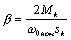(4.21) - модуль жесткости линеаризованной механической характеристики.
Пределы целесообразного использования этого выражения ограничиваются значениями момента
.
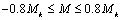Структурная схема асинхронного электромеханического преобразователя, линеаризованного в пределах рабочего участка механической характеристики двигателя, имеет вид (рис. 4.10):
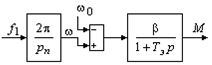
Рис. 4.10. Структурная схема асинхронного электромеханического преобразователя с линеаризованной механической характеристикой.
Эта структура показывает, что изменения скорости электропривода для электромеханического преобразователя являются возмущениями, определяющими изменения электромеханического момента при данном управляющем воздействии.
Передаточная функция электромеханического преобразователя по возмущению называется динамической жесткостью механической характеристики:
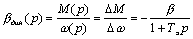(4.22)
Сравнивая уравнение механической характеристики асинхронного двигателя с аналогичными характеристиками двигателя постоянного тока с независимым возбуждением, можно заключить, что в пределах рабочего участка асинхронный двигатель имеет динамические свойства аналогичные двигателю постоянного тока с независимым возбуждением.
Так как критическое скольжение двигателей лежит в
пределах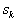 
=0.05..0.5, причем меньшие значения соответствуют более
мощным двигателям, электромагнитная постоянная Тэпри питании от источника напряжения
невелика:
,
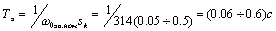(меньшие значения соответствуют двигателям малой мощности).
В случае питания асинхронного электромеханического преобразователя от источника тока выражение для его механической характеристики будет иметь вид:
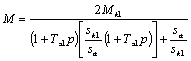(4.23)
где
.
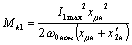Уравнение критического момента для трехфазной машины получим, заменив максимальное значение тока обобщенной машины I1 max действующим значением тока фазы трехфазного двигателя I1 с помощью уже применявшейся формулы:
.
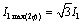Выполнив эту замену, получим:
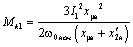(4.24)
Сравнив выражения механической характеристики асинхронной машины для двух случаев питания, можно установить, что они совпадают по форме и отличаются лишь выражениями критического момента и электромагнитной постоянной времени.
Следовательно, выполнив линеаризацию механической характеристики, получим приближенное линеаризованное уравнение:
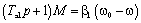(4.25)
где
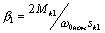(4.26) - жесткость механической характеристики асинхронной машины при ее питании от
источника тока.
Передаточная функция динамической жесткости:
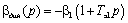(4.27)
Структурная схема электромеханического преобразователя энергии при питании от источника тока (рис.4.11)
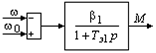
Рис. 4.11. Структурная схема электромеханического преобразователя энергии при питании от источника тока.
совпадает с аналогичной схемой для случая его питания от источника напряжения. Однако динамические свойства в этих режимах существенно отличаются в связи с тем, что при питании от источника тока поток, при I1=const, изменяется в широких пределах. Поэтому инерционность электромеханического преобразователя в случае питания от источника тока существенно выше.
;
.
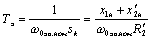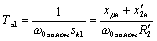Так как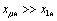 
, то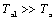 
.