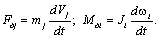 (2.37)
(2.37)
Правые части полученных выше уравнений движения электропривода представляют собой моменты инерции действующих сил в системе. В теории электропривода эти силы и моменты принято называть динамическими:
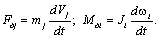 (2.37)
(2.37)
Уравнение движения приведённого жёсткого механического звена определяет суммарную динамическую нагрузку электропривода:
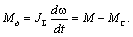 (2.38)
(2.38)
Нагрузки механического оборудования определяют его износ; причём наиболее неблагоприятно влияние нагрузок, содержащих знакопеременную составляющую. Поэтому ограничение максимальных нагрузок и уменьшение динамических колебательных нагрузок, обусловленных упругими связями, обеспечивает повышение надёжности и долговечности.
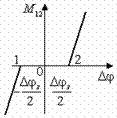
Динамические нагрузки в реальных установках в значительной мере возрастают из-за ударов, возникающих при выборе зазоров в передачах и сочленениях рабочего оборудования. С учётом кинематических зазоров двухмассовая схема механической части имеет вид:
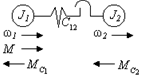
a) б)

в)
Рис. 2. 20. К анализу динамических нагрузок механической части с учетом зазоров в передачах ((а) – расчетная двухмассовая схема механической части с учетом кинематических зазоров; (б) – зависимость момента упругого взаимодействия между движущимися массами системы от угла поворота с учетом кинематических зазоров; (в) – структурная схема механической части электропривода с учетом механических зазоров).
Уравнения движения для этой системы имеют вид:
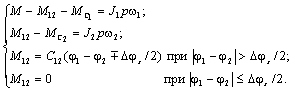
Из структурной схемы и уравнений движения видно, что при разомкнутом зазоре массы движутся независимо. Так как при этом М12=0, то при М=М1=const уравнения примут вид:
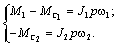
Как следствие,
к моменту соударения масс скорости ω1
и ω2 могут существенно отличаться.
Так, при реактивном 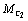 на первом этапе пуска (М12=0)
скорость ω2=0, а скорость ω1 быстро увеличивается, т.к.
на первом этапе пуска (М12=0)
скорость ω2=0, а скорость ω1 быстро увеличивается, т.к. 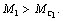 К моменту окончания выбора зазоров она успевает вырасти до
значения:
К моменту окончания выбора зазоров она успевает вырасти до
значения:
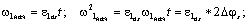
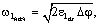
где
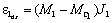 - ускорение при выборе зазоров.
- ускорение при выборе зазоров.
При реактивном
характере момента 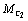 после выбора зазора скорость
после выбора зазора скорость 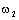 будет оставаться равной нулю до тех пор, пока момент М12 возрастая, не превысит
значения
будет оставаться равной нулю до тех пор, пока момент М12 возрастая, не превысит
значения 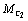 . За время нарастания момента M12 до
. За время нарастания момента M12 до 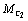 скорость ω1
дополнительно увеличится до значения
скорость ω1
дополнительно увеличится до значения 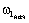 , которое, в конечном счёте, и определит динамическую
нагрузку передач после трогания второй массы.
, которое, в конечном счёте, и определит динамическую
нагрузку передач после трогания второй массы.
Из физических
соображений можно заключить, что накопленная за время выбора зазора первой
массы кинетическая энергия 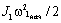 должна при ударе
реализоваться в дополнительных нагрузках передач. Для количественного анализа
получим зависимость М12=f(t) для третьего этапа процесса,
когда
должна при ударе
реализоваться в дополнительных нагрузках передач. Для количественного анализа
получим зависимость М12=f(t) для третьего этапа процесса,
когда 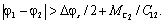
На третьем этапе уравнения движения можно представить в виде:
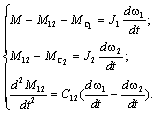
Умножим первое уравнение на 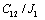 , а второе на
, а второе на 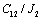 , а затем вычтем из первого
уравнения второе. Тогда, с учетом третьего выражения, правая часть становится
равной
, а затем вычтем из первого
уравнения второе. Тогда, с учетом третьего выражения, правая часть становится
равной 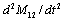 и после преобразований можно записать
и после преобразований можно записать
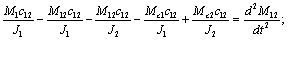
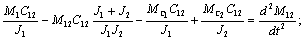
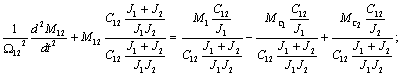
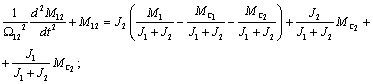
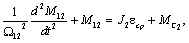
где
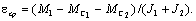
С учётом проведённого анализа предыдущих этапов выбора зазоров решение полученного уравнения следует искать при следующих начальных условиях (t=0):
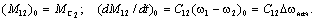
Общее решение
уравнения с учётом определяемого правой частью частного решения и корней 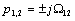 запишем в виде:
запишем в виде:
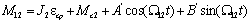 .
.
Для
определения коэффициентов 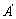 и
и 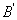 используем начальные условия:
используем начальные условия:
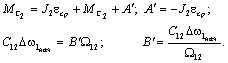 .
.
Следовательно,
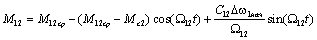 .
.
где
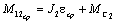 .
.
После преобразований получим:
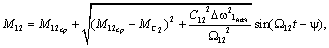 (2.39)
(2.39)
где
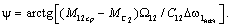 (2.40)
(2.40)
В соответствии с полученным выражением максимум нагрузки передач в рассматриваемом переходном процессе определяется соотношением:
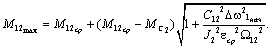 (2.41)
(2.41)
Таким образом,
динамические нагрузки, обусловленные упругими колебаниями, существенно
увеличивают нагрузки передач. При отсутствии колебательной составляющей в
выражении для М12 момент
нагрузки передач в процессе пуска равен 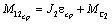 . За счёт упругих колебаний в соответствии с выражением для
(2.40) нагрузка возрастает; её превышение над средней нагрузкой называется
динамическим коэффициентом:
. За счёт упругих колебаний в соответствии с выражением для
(2.40) нагрузка возрастает; её превышение над средней нагрузкой называется
динамическим коэффициентом:
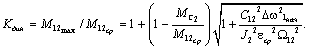 (2.42)
(2.42)
При
пуске с предварительно выбранными зазорами и выполнении равенства 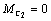 (и
(и 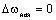 ) динамический коэффициент Кдин=2, т.е. упругие колебания вдвое увеличивают рабочие
нагрузки передач:
) динамический коэффициент Кдин=2, т.е. упругие колебания вдвое увеличивают рабочие
нагрузки передач:
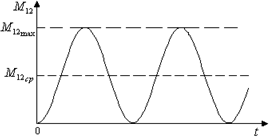
Рис.
2.21. Динамические нагрузки передач при пуске электропривода с
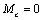 и
и 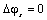 .
.
При наличии
зазоров (т.е.
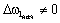 ) максимум нагрузок возрастает и может достигнуть опасных для
механической прочности передач значений. Если в формуле (2.42) для
) максимум нагрузок возрастает и может достигнуть опасных для
механической прочности передач значений. Если в формуле (2.42) для
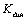 ,
выполнить преобразования:
,
выполнить преобразования:
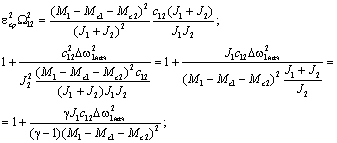
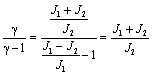
и учесть, что
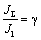
то выражение (2.42) для динамического коэффициента можно записать в виде:
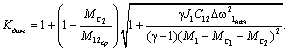
Нетрудно
видеть, что динамические коэффициенты, обусловленные упругими ударами, при
выборе зазоров тем больше, чем больше момент инерции ротора двигателя и жестко
с ним связанных элементов
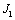 и чем больше жесткость
механической связи.
и чем больше жесткость
механической связи.
При условии,
что
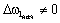 упругость передачи
является фактором, снижающим динамические нагрузки. В этом можно убедиться,
подставив в последнее выражение значение С12=∞
- ему соответствуют бесконечно большие динамические коэффициенты. Однако при
реальных конечных значениях С12
удары при выборе зазоров могут создавать недопустимые нагрузки или существенно
увеличивать износ механического оборудования. В этих случаях при проектировании
электропривода предусматриваются законы управления, обеспечивающие повышение
плавности выбора зазоров и снижение ударных нагрузок до допустимых значений
путём ограничения достигаемой при выборе зазоров скорости
упругость передачи
является фактором, снижающим динамические нагрузки. В этом можно убедиться,
подставив в последнее выражение значение С12=∞
- ему соответствуют бесконечно большие динамические коэффициенты. Однако при
реальных конечных значениях С12
удары при выборе зазоров могут создавать недопустимые нагрузки или существенно
увеличивать износ механического оборудования. В этих случаях при проектировании
электропривода предусматриваются законы управления, обеспечивающие повышение
плавности выбора зазоров и снижение ударных нагрузок до допустимых значений
путём ограничения достигаемой при выборе зазоров скорости
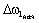 .
.
Динамические колебательные процессы в среднем не влияют на длительность переходных процессов пуска, реверса и торможения электропривода. Однако они во многих случаях отрицательно сказываются на условиях выполнения технологических операций, особенно на точности работы установки. Возникающие колебания практически всегда увеличивают динамические нагрузки и ускоряют его износ, т.е. являются одним из факторов, определяющих надёжность, долговечность и производительность машин.
Динамический коэффициент является важной характеристикой условий работы механического оборудования, а его значения определяются, главным образом, динамическими свойствами электропривода. При проектировании и наладке электроприводов задача уменьшения динамического коэффициента до значений, близких к единице, имеет большое значение. Для многих механизмов она определяет выбор структуры, настроек и параметров электропривода и при успешном решении обеспечивает увеличение срока службы механического оборудования.