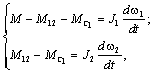
Полученные уравнения движения позволяют проанализировать механическую часть электропривода, как объект системы автоматического регулирования и управления и представить его в виде динамического звена.
Воспользовавшись уравнением движения двухмассовой механической системы (2.21):
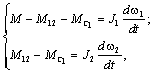
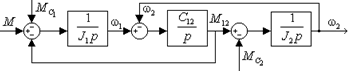
структурную схему двухмассовой упругой механической части без учёта внутреннего демпфирования можно представить в виде (рис.2.12):
а)
б)
в)
г)
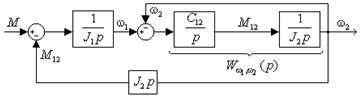
Рис. 2.12. Структурные схемы двухмассовой упругой механической части электропривода без учета внутреннего демпфирования
Для исследования свойств
рассматриваемой системы примем возмущения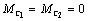 
и перенесём внутреннюю
связь по упругому моменту на выход системы (рис. 2.12б).
Теперь нетрудно определить передаточную функцию, связывающую выходную координату со скоростью ω1:
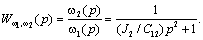
В соответствии со схемой рис. 2.12б передаточная функция прямого канала для координаты ω1:
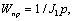
а обратной связи:
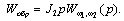
Следовательно, искомая передаточная функция определится как (рис. 2.13):
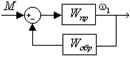
Рис. 2.13. Передаточная функция замкнутой системы.
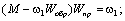
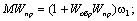
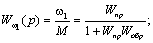
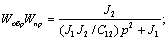
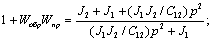
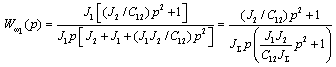
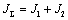
Следовательно, искомая передаточная функция может быть записана в виде:
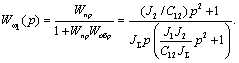(2.24)
Характеристическое уравнение системы:
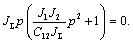
Корни характеристического уравнения:
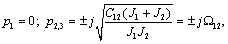
где
Ω1,2 – резонансная частота двухмассовой упругой системы.
Введём следующие обобщенные параметры двухмассовой упругой системы:
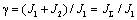- соотношение масс;
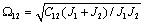- резонансная частота системы;
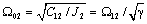- резонансная частота второй массы при жёсткой заделке первой ( 
).
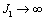С учётом этих обозначений можно записать:
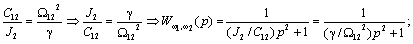
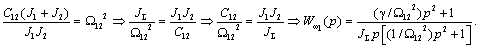
Таким образом, имеем:
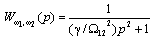(2.25)
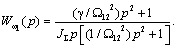(2.26)
Полученные
соотношения позволяют представить механическую часть как объект управления в
виде трёх звеньев, показанных на рис. 2.12в. Из этой схемы находим передаточную функцию системы по
управляющему воздействию при выходной переменной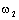 
:
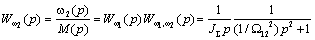(рис.2.12г)
Для
анализа системы найдём амплитудо-частотную (АЧХ) и фазо-частотную (ФЧХ)
характеристики, для чего подставим (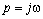 
) в выражение для выражения 
:
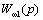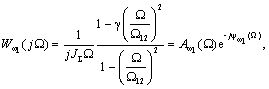(2.27)
где
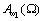- АЧХ;
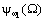- ФЧХ.
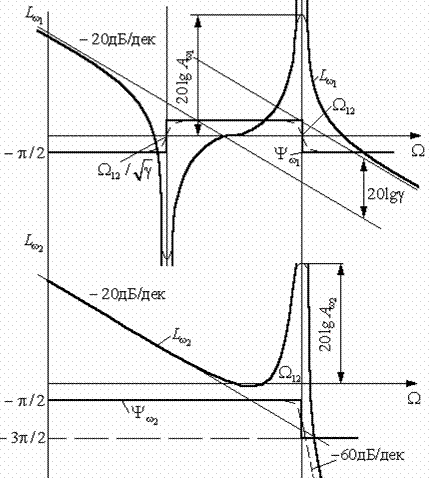
Асимптотические логарифмические характеристики могут быть построены непосредственно по полученным передаточным функциям (рис. 2.14).
В соответствии с выражением для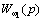 
система может быть представлена последовательным соединением
интегрирующего звена, формирующего звена второго порядка с частотой сопряжения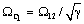 
и идеального
колебательного звена с резонансной частото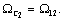й 
. При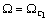 
имеет место нуль передаточной функции и ЛАЧХ терпит разрыв,
стремясь к (-∞) (lg0→-∞). При Ω=Ω12 имеет место полюс передаточной функции
и амплитуды стремятся к (+∞), образуя второй разрыв.
Низкочастотная асимптота определяется интегрирующим звеном с коэффициентом,
обратно пропорциональным JΣ и
соответственно имеет наклон –20 дБ/дек. Высокочастотная асимптота (Ω»Ω12)
соответствует также интегрирующему звену, но при коэффициенте в γ раз большем, чем в области низких частот. В этом
можно убедиться, устремив в ∞ частоту Ω в
(2.27).
В
низкочастотной области сдвиг между колебаниями составляет -90˚
и определяется интегрирующим звеном. При значениях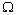 
, соответствующих выражению 
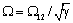, меняет знак числитель выражения (2.27), что соответствует
уменьшению фазового сдвига на 180˚ . Затем на частоте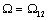 
аналогично изменяется
знак знаменателя, и фазовый сдвиг вновь принимает значение -90˚
в соответствии с высокочастотной асимптотой ЛАЧХ.
На рис. 2.14б
представлены логарифмические характеристики механической части электропривода
по управлению по выходной переменной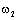 
. Они построены по передаточной функции 
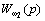. В низкочастотной области ЛАЧХ 
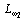совпадает с 
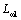, разрыв имеет место только на резонансной частоте 
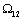и в высокочастотной
области стремится к асимптоте с наклоном -60дБ/дек. Соответственно фазовый
сдвиг при этом составляет -270˚.
Проанализируем
основные свойства механической части, воспользовавшись ее структурной схемой и
частотными характеристиками. При этом обратим внимание на различие во влиянии
упругости на движение первой и второй масс. Движение первой массы при небольших
частотах колебаний управляющего воздействия М определяется суммарным моментом
инерции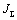 
, причем механическая часть ведет себя как интегрирующее
звено. В частности, при M=const скорость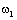 
изменяется по
линейному закону, на который накладываются колебания, обусловленные обратной
связью. Иными словами, интегрирующее звено характеризует условия движения
механической части в среднем.
При
приближении частоты колебаний момента к резонансной 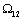, амплитуды колебаний скорости 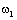возрастают и при выполнении равенства 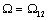стремятся к бесконечности.
Проявления
резонанса существенно зависят от параметров механической части в связи с
наличием в числителе передаточной функции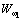 
форсирующего звена второго порядка. Можно выявить условия,
при выполнении которых влияние упругости на движение первой массы будет
незначительным.
Во-первых, из
выражения (2.27) непосредственно следует, что если механизм обладает небольшой
инерцией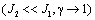 
, то движение первой массы близко к движению, определяемому
интегрирующим звеном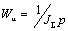 
. Во-вторых, из (2.27) видно, что при значениях 
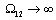в области малых и
средних частот движение первой массы определяется тем же интегрирующим звеном.
Отсюда вытекает важный практический вывод.
Если при
синтезе электропривода используются обратные связи только по переменным
двигателя, то при значениях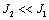 
или 
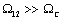, где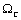 
- частота среза желаемой ЛАЧХ разомкнутого контура
регулирования, механическую часть электропривода можно представить жестким
механическим звеном, не учитывая влияния упругостей (рис. 2.15).
В соответствии
с передаточной функцией 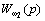и рис. 2.14б, колебательность
второй массы выше, чем первой. В низкочастотной области
асимптоты ЛАЧХ 
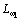и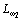 
совпадают, т.к. в среднем движение второй массы, как и
первой, определяется действием интегрирующего звена 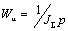. Однако при 
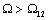наклон высокочастотной
асимптоты 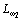составляет -60дБ/дек и
нет факторов, противодействующих развитию резонансных явлений при любых γ.
а)
б)
Рис. 2.14.
Логарифмические частотные характеристики двухмассовой
упругой системы по управляющему воздействию (а - при выходной переменной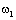 
; б - при выходной переменной ).
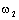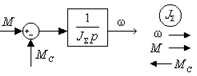
Рис. 2.15. Структурная схема механической части электропривода с жесткими механическими связями.
Следовательно, во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругости механических связей нельзя.
Учет естественного демпфирования существенно не сказывается на форме ЛАЧХ и ЛФЧХ системы, однако ограничивает резонансный пик конечными значениями (как показано на рисунках 2.14а и 2.14 б).
Сочетания параметров,
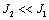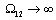при которых или достаточно
распространены. Поэтому во многих случаях, когда это допустимо, используется
представление механической части в виде жесткого приведенного звена.