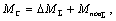(2.9)
Кроме электромагнитного момента на механическую часть электропривода действуют статические нагрузки, которые делятся на силы и моменты механических потерь и силы и моменты полезных нагрузок исполнительных механизмов:
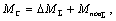(2.9)
где первая составляющая суммы является суммарными потерями в двигателе и в исполнительном механизме, а вторая – суммарным приведённым моментом полезной нагрузки.
По характеру взаимодействия с электроприводом различаются активные и реактивные силы и моменты.
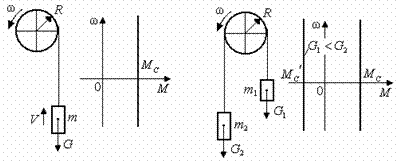
Активными силами и моментами называются силы и моменты, величина и направление которых не зависит от движения электропривода; например, силы и моменты, создаваемые перемещаемым по вертикали грузом. Механическая характеристика такого вида статической активной нагрузки изображена на рис. 2.5.
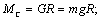
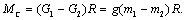
a) б)
Рис. 2.5. Активные нагрузки электропривода неуравновешенного (а) и уравновешенного (б) подъемных механизмов.
В зависимости от соотношения масс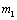 
и 
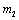двигатель работает в тормозном ( 
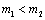) или двигательном ( 
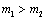) режимах.
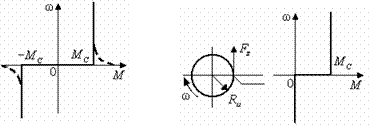
Силы и моменты, возникающие как реакции на движение электропривода, называются реактивными. Направление их всегда противоположно направлению движению электропривода. По характеру зависимости от скорости реактивных сил и моментов различают нагрузки типов сухого трения (рис. 2.6):
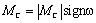
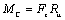
a) б)
Рис.
2.6. Реактивные нагрузки: сухое трение (а) и момент резания (б).
В момент трогания силы сухого трения могут превышать свои значения при движении (рис. 2.6а).
Силы и моменты вязкого трения зависят от скорости линейно (рис. 2.7):
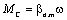(2.10)
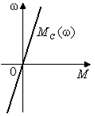
Рис.
2.7. Момент нагрузки типа вязкого трения.
Момент внутреннего вязкого трения:
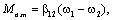(2.11)
где
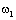и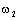 
– скорости на входе и
выходе деформируемого элемента.
По характеру влияния на механические колебания все силы и моменты делятся на консервативные и диссипативные.
При действии консервативных сил и моментов не происходит поглощение колебаний. Например, сила тяжести является консервативной силой, т. к. работа, осуществляемая этой силой за период колебаний, всегда равна нулю.
При действии диссипативных сил происходит
поглощение энергии колебаний. Примером является вязкое трение, т.к. при
изменении знака скорости изменяется и знак момента, а механическая мощность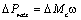 
сохраняет
положительный знак, что соответствует поглощению колебаний.
На практике распространённой является вентиляторная нагрузка (рис. 2.8):
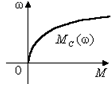
Рис. 2.8. Зависимость момента от скорости при вентиляторной нагрузке
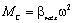(2.12)
Коэффициент полезного действия (КПД) механизма: ηмех=η1η2η3 .., где η1, η2, η3 – КПД элементов кинематической цепи.
Если известен полезный момент нагрузки механизма Mмех, то для прямого направления энергии приведённый к валу двигателя момент статической нагрузки можно определить из равенства:
( 
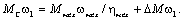
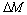– момент механических потерь в двигателе.)
Следовательно,
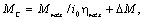(2.13)
где
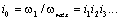- общее передаточное число от двигателя к рабочему органу
механизма.
При обратном направлении потока энергии, когда нагрузка является активной и двигатель должен работать в тормозном режиме, уравнение баланса мощностей можно записать как:
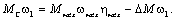
В этом случае
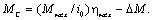(2.14)
Момент
механических потерь в двигателе невелик, он составляет 1-5% номинального
момента двигателя. Во многих практических случаях полагают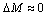 
, т.к. точность определения момента Mмех невелика и он
рассчитывается с некоторым запасом. При этом формулы приведения момента статической
нагрузки к валу двигателя принимают вид:
- для прямого направления передачи энергии (двигательный режим работы)
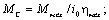(2.15)
- для обратного направления (тормозной режим работы)
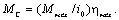(2.16)
Если рабочий орган движется поступательно, то уравнение баланса мощностей имеет вид (ΔМ=0):
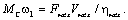
Тогда
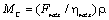(2.17)
Соответственно для обратного направления потока механической энергии
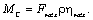(2.18)
Необходимо иметь в виду, что КПД передач зависит от нагрузки, а для червячного зацепления – и от направления передачи энергии, поэтому при расчётах следует использовать соответствующие зависимости η от полезной нагрузки передач.