Перейдем к рассмотрению переходных процессов в цепи с последовательным соединением резистора  и емкости . По второму закону Кирхгофа для этой цепи

Ток в емкости можно представить в виде . Отсюда

.

Решение этого дифференциального уравнения для напряжения на емкости также можно представить суммой свободной и установившейся составляющих . Свободную составляющую найдем из решения однородного уравнения () в виде . Подставим это выражение в уравнение и найдем значение

Выражение  представляет собой характеристическое уравнение, которое могло быть получено без подстановки общего выражения для свободной составляющей формальной заменой в однородном дифференциальном уравнении производных от напряжения на емкости на , где  - порядок производной.

Отсюда общее решение для напряжения на емкости

                (1)

где  - постоянная интегрирования, определяемая из начальных условий; - постоянная времени переходного процесса.

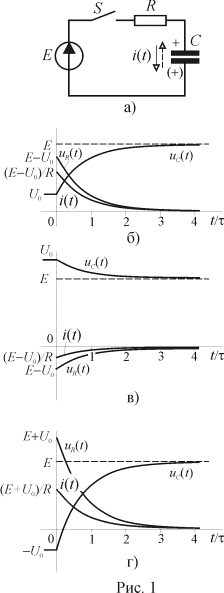Рассмотрим процесс подключения последовательной  цепи к источнику постоянной ЭДС  (рис. 1 а).

В отличие от индуктивности, емкость после накопления заряда может длительное время сохранять его. Поэтому начальное значение напряжения на емкости  может быть произвольным и иметь произвольный знак по отношению к ЭДС источника.

Установившееся значение напряжения на емкости после замыкания ключа   всегда будет равно , т.к. на постоянном токе в установившемся режиме  и , а . Поэтому из выражения (1) напряжение на емкости в общем виде будет равно

     (2)

Пусть напряжение на емкости до коммутации было  (знак + соответствует полярности напряжения на рис. 1 а без скобок). Тогда из выражения (2) для момента времени непосредственно после замыкания ключа найдем постоянную

,

а затем и выражение для напряжения на емкости в виде

           (3)

где - постоянная времени переходного процесса.

Отсюда можно найти ток в цепи и падение напряжения на резисторе

На рис. 1 б-г приведены временные диаграммы переходного процесса подключения  цепи к источнику постоянной ЭДС для трех вариантов начальных значений напряжения на емкости: 1) ; 2)  и 3)  Во всех случаях напряжение на емкости монотонно по экспоненте изменяется от до . В то время как ток и напряжение на резисторе в момент коммутации скачкообразно изменяются на величину пропорциональную разности или сумме  и , а затем монотонно уменьшаются до нуля. При этом если , то ток и падение напряжения на R отрицательны, т.е. происходит разряд емкости.

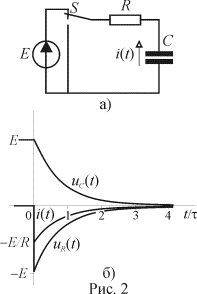Полный разряд емкости происходит при отсутствии внешних источников энергии (рис. 2 а). После переключения ключа  вся энергия, накопленная в электрическом поле емкости , преобразуется в тепло в резисторе .

Напряжение на емкости в переходном процессе будет иметь только свободную составляющую

и если цепь достаточно длительное время была подключена к источнику, то в момент переключения напряжение на емкости будет равно . Поэтому постоянная интегрирования  будет равна

,

а напряжение на емкости в переходном процессе –

Отсюда ток в цепи и напряжение на резисторе

Из этих выражений следует, что напряжение емкости после коммутации монотонно без разрывов спадает до нуля по экспоненте с постоянной времени  (рис. 2 б), в то время как, ток в цепи и напряжение на сопротивлении в момент коммутации скачкообразно изменяются, а затем также спадают до нуля. Отрицательное значение тока и напряжения на сопротивлении означает, что их направление противоположно направлению тока при заряде емкости.

Проверка решения по второму закону Кирхгофа дает очевидное тождество

.