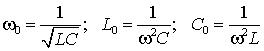Явление резонанса относится к наиболее важным с практической точки зрения явлениям в электрических цепях. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.

Общее условие резонанса для любого двухполюсника можно сформулировать в виде  или , где  и  комплексные сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.

Для определения условий возникновения режима резонанса в электрической цепи нужно:

Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.

Уравнение  может иметь несколько решений относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех его значениях имеющих физический смысл.

В электрических цепях резонанс может рассматриваться в задачах:

Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми характеристиками.

Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром. Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным, и оно может отсутствовать в цепи как отдельный элемент (резистор). Однако при определенных условиях его следует учитывать.

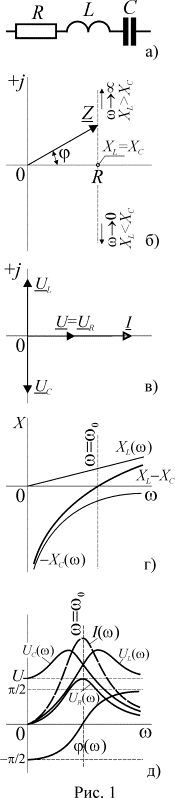Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно

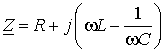
Из этого выражения условие резонанса будет иметь вид

Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления  когда индуктивное сопротивление  равно емкостному . Это состояние может быть получено вариацией любого их трех параметров - ,  и , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде

.

Частота  называется резонансной или собственной частотой цепи.

При резонансе векторы  и  равны по величине и направлены встречно друг другу (рис. 1 в). Поэтому вектор входного напряжения равен напряжению на сопротивлении .

Рассмотрим процессы в контуре при изменении частоты питания.

При изменении частоты резистивная составляющая комплексного сопротивления цепи  остается постоянной, а реактивная изменяется. Поэтому конец вектора  на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку  вещественной оси (рис. 1 б). В режиме резонанса мнимая составляющая  равна нулю и , т.е. полное сопротивление при резонансе соответствует минимальному значению и равно резистивной составляющей комплексного сопротивления.

Индуктивное  и емкостное сопротивления являются частотно-зависимыми параметрами и изменяются так, как показано на рис. 1 г. Равенство сопротивлений  и  наступает в режиме резонанса при частоте . При частотах ниже резонансной частоты реактивное сопротивление контура  имеет емкостной характер, а при частотах превышающих резонансную– индуктивный (рис. 1 г).

При постоянном напряжении на входе контура  изменение сопротивления будет приводить к изменению тока, а т.к. при резонансе полное сопротивление минимально, то ток будет максимальным и равным  (рис. 1 д). По этому признаку с помощью амперметра можно определить режим резонанса. Кривую

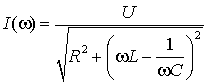
принято называть амплитудно-частотной характеристикой или резонансной кривой тока.

Частотная зависимость фазового сдвига тока относительно напряжения

называется фазо-частотной или фазовой характеристикой (рис. 1 д). При частоте стремящейся к нулю , и . При бесконечном возрастании частоты - , а .

При изменении частоты изменяются также падения напряжения на элементах контура (рис. 1 д). Напряжение на сопротивлении  повторяет в некотором масштабе резонансную кривую тока , достигая при резонансной частоте максимума, равного входному напряжению . Частотные характеристики  и  легко получить с помощью закона Ома

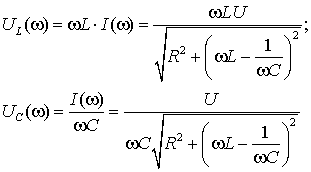
Они имеют одинаковые максимумы, расположенные слева и справа от резонансной частоты.

Определим напряжения на элементах контура в режиме резонанса. По закону Ома, с учетом полученных ранее соотношений, они равны

где 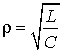- величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.

Следовательно, при резонансе

Отношение волнового сопротивления к резистивному , называется добротностью контура, а величина обратная  - затуханием. Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому в режиме резонанса на реактивных элементах цепи могут возникать опасные перенапряжения. Усиление напряжения является особенностью режима резонанса в последовательном контуре, вследствие чего этот вид резонанса получил название резонанса напряжений.

 

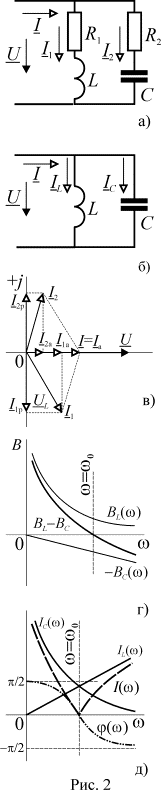Параллельный резонансный контур может содержать резистивные сопротивления (рис. 2 а), соответствующие потерям энергии в катушке индуктивности и конденсаторе. В этом случае комплексные проводимости ветвей будут равны , где

,

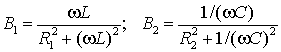а общая проводимость .

Отсюда условие резонанса

.

Раскрывая это выражение, получим резонансную частоту

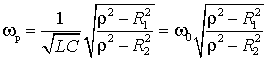                          (1)

где 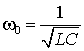- резонансная частота в параллельном контуре без потерь (рис. 2 б), т.е. при , а 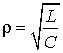- волновое сопротивление параллельного контура без потерь.

Из выражения (1) следует, что резонанса можно достичь изменением пяти параметров .

Наличие в выражении (1) множителя при  создает ряд особенностей резонанса в этой цепи. При разных резистивных сопротивлениях  резонанс возможен только, если оба сопротивления одновременно больше или меньше . В противном случае выражение под корнем отрицательно, резонансная частота мнимая и не имеет физического смысла.

Если , то , т.е. резонанс наступает при той же частоте, что и в простейшем контуре без потерь (рис. 2 б).

Однако при этом условии возможен вариант, когда . В этом случае подкоренное выражение в (1) становится неопределенным (0/0) и это означает, что резонанс может наступать при любой частоте. Входное сопротивление контура при этом чисто активное и равно .

На рис. 2 в приведена векторная диаграмма цепи в режиме резонанса. Из нее следует, что входной ток контура равен сумме активных составляющих токов первой и второй ветви, которые определяются величиной активных сопротивлений. В идеальном случае отсутствия потерь (, рис. 2 б) входной ток становится равным нулю и входное сопротивление цепи равным бесконечности. При этом токи в индуктивности и емкости могут быть весьма значительными. Поэтому резонанс в параллельном контуре называют резонансом токов.

Для идеализированного контура характер частотных зависимостей реактивных проводимостей показан на рис. 2 г. При низких частотах до резонансной частоты проводимость цепи имеет индуктивный характер, а при частотах выше резонансной – емкостной.

На рис 2 д показаны частотные характеристики контура без потерь. При постоянном входном напряжении зависимости токов от частоты определяются законом Ома

.

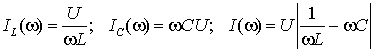Фазо-частотная характеристика  при отсутствии потерь в контуре представляет собой константу , скачкообразно изменяющую знак при резонансной частоте. При учете потерь эта характеристика имеет вид, показанный на рис. 2 д.