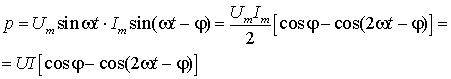Понятие потенциала или разности потенциалов u позволяет определить работу, совершаемую электрическим полем при перемещении элементарного электрического заряда , как . В то же время, электрический ток равен . Отсюда , следовательно, скорость совершения работы, т.е. мощность в данный момент времени или мгновенная мощность равна

                                                       (1)

где  и  - мгновенные значения напряжения и тока.

Величины тока и напряжения, входящие в выражение (1), являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной и для ее оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период  работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.

.

Пусть  и , тогда мгновенная мощность будет равна

,            (2)

а средняя мощность –

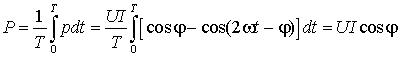.                         (3)

Величина  называется коэффициентом мощности.

Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока  и напряжения , но и от разности фаз  между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению . При сдвиге фаз между током и напряжением в  средняя мощность равна нулю. Максимальные значения напряжения и тока любой электрической машины определяются ее конструкцией, а максимальная мощность, которую они могут развивать - произведением этих величин. Если электрическая цепь построена нерационально, т.е. сдвиг фаз  имеет значительную величину, то источник электрической энергии и нагрузка не могут работать на полную мощность. Поэтому в любой системе источник-нагрузка существует т.н. "проблема ", которая заключается в требовании возможного приближения коэффициента мощности к единице.

Выражение (3) можно представить также с помощью понятий активных составляющих тока  и напряжения  в виде

                           (4)

Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную составляющую комплексного сопротивления цепи как  или , выражение (4) можно записать также в форме

Среднюю мощность  называют также активной мощностью и измеряют в ваттах [Вт].

Из выражения (2) следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей  равной средней или активной мощности.

При  () , т.е. для цепи, обладающей чисто резистивным сопротивлением справедливы выражения

                                                  (5)

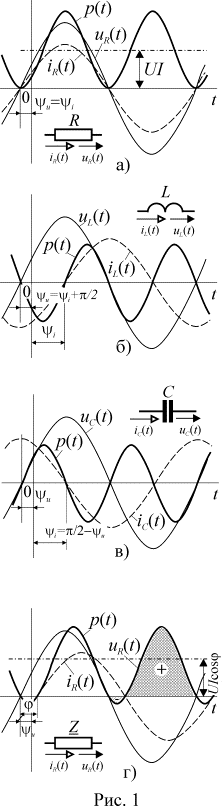Временные диаграммы, соответствующие этому случаю приведены на рис. 1 а.

Положительные значения мгновенной мощности соответствуют поступлению энергии от источника в электрическую цепь. Следовательно, при резистивной нагрузке вся энергия поступающая от источника преобразуется в ней в тепло.

При  () , т.е. для чисто реактивной цепи

               (6)

Временные диаграммы, соответствующие чисто индуктивной и чисто емкостной нагрузке приведены на рис. 1 б и в. Из выражений (6) и временных диаграмм следует, что мощность колеблется относительно оси абсцисс с двойной частотой, изменяя свой знак каждые четверть периода. Это означает, что в течение четверти периода () энергия поступает в электрическую цепь от источника и запасается в магнитном или электрическом поле, а в течение следующей четверти () она целиком возвращается из цепи в источник. Так как площади, ограниченные участками с положительной мощностью и с отрицательной одинаковы, то средняя мощность отдаваемая источником нагрузке равна нулю и в цепи не происходит преобразования энергии.

В общем случае произвольной нагрузки  () и

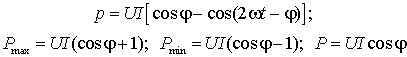Как следует из временных диаграмм рис. 1 г, большую часть периода мощность потребляется нагрузкой (), но существуют также интервалы времени, когда энергия запасенная в магнитных и электрических полях нагрузки возвращается в источник. Участки с положительным значением  независимо от характера реактивной составляющей нагрузки всегда больше участков с отрицательным значением, поэтому средняя мощность P положительна. Это означает, что в электрической цепи преобладает процесс преобразования электрической энергии в тепло или механическую работу.

Как уже отмечалось выше, средняя за период мощность реактивных элементов цепи равна нулю, т.к. в течение четверти периода энергия потребляется от источника питания цепи и накапливается в магнитном или электрическом полях, а в следующую четверть целиком отдается в источник. Однако проанализировать обмен энергией между источником питания и реактивными элементами цепи возможно только в простейших случаях. На практике для оценки энергии, не преобразуемой в электрической цепи, пользуются понятием реактивной мощности, которая вычисляется по формуле

и является мерой потребления реактивного тока.

Реактивную мощность также можно представить через реактивные составляющие тока или напряжения

В отличие от всегда положительной активной мощности, реактивная мощность положительна при  и отрицательна при .

Кроме активной и реактивной мощности в цепях переменного тока пользуются понятием полной или кажущейся мощности . Физического смысла это понятие не имеет, но может быть определено как максимально возможная активная мощность, т.е. мощность чисто резистивной цепи при данном напряжении и токе ().

Между активной реактивной и полной мощностью существуют очевидные соотношения

, образующие понятие комплексной мощности  и треугольника мощностей, который можно описать с помощью комплексных чисел и изобразить векторами на комплексной плоскости в виде

где - сопряженный комплексный ток.

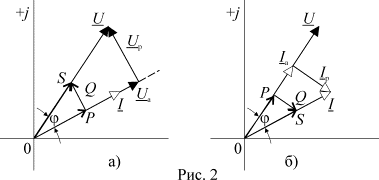Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4)), треугольник мощностей можно построить в двух вариантах (рис. 3 а и б). В первом случае активная и реактивная составляющие полной мощности выражаются через активную и реактивную составляющие напряжения  и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а). Во втором случае (рис. 2 б), построение выполнено с помощью активной и реактивной составляющих тока .

Очевидно, что все виды мощности имеют одинаковую размерность, поэтому для их отличия от активной мощности, измеряемой в ваттах [Вт], для полной мощности введена единица, называемая вольт-амперы [ВА], а для реактивной мощности - вольт-амперы реактивные [ВАр]

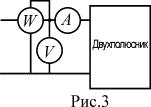Выражение для активной мощности  позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.

Для этого на вход цепи включают приборы по схеме рис. 3 и по их показаниям определяют коэффициент мощности в виде

где ,  и  - мощность, напряжение и ток, отсчитанные по показаниям соответственно ваттметра , вольтметра и амперметра  действующих значений. Из этого выражения можно также определить угол сдвига фаз  между током и напряжением на входе двухполюсника.