В любой электрической цепи независимо от ее состояния и характера внешнего воздействия в каждый момент времени должны выполняться условия, формулируемые как законы Кирхгофа. Это связано с тем, что эти законы являются одной из форм общего закона сохранения энергии и, следовательно, не допускают каких-либо исключений.

В цепях переменного тока условия законов Кирхгофа для узлов и контуров можно записать для мгновенных значений токов и напряжений точно так же, как это было обосновано и сделано для цепей постоянного тока, т.е. в виде

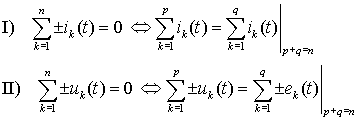
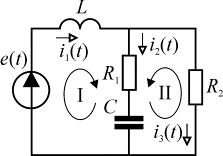(1)

Различие для цепей постоянного и переменного токов заключается только в том, что в цепях переменного тока направления токов, напряжений и ЭДС, указываемые на схемах электрической цепи, считают условно положительными. В остальном алгоритм их составления полностью идентичен. Рассмотрим его на примере цепи приведенной на рисунке.

Токи и ЭДС в этой цепи являются синусоидальными функциями времени. Произвольно зададим положительные направления токов во всех трех ветвях. Положительное направление ЭДС источника так же как в цепях постоянного тока указывает стрелка условного обозначения.

Исходная цепь не содержит источников тока, поэтому общее число уравнений равно числу ветвей. Из них одно уравнение можно составить, пользуясь первым законом Кирхгофа, и два – вторым.

В соответствии с выбранными положительными направлениями токов

.

Для составления уравнений по второму закону произвольно выберем два замкнутых контура ( и ) так, чтобы каждая ветвь была включена, по крайней мере, в один контур. Произвольно зададим направления обхода контуров (см. рис.) и составим для них уравнения, используя выражения для падений напряжения на элементах цепи,

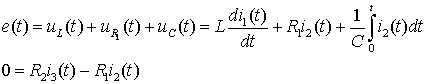
Решение этих уравнений во временной области (для синусоидальных функций) обычно затруднительно. Поэтому их преобразуют в символическую форму, находят решение для изображений искомых величин, а затем преобразуют их к оригиналам функций.

Используя понятия комплексных сопротивлений можно составлять уравнения Кирхгофа сразу в символической форме, минуя этап составления уравнений во временной области. Такой порядок расчета для рассмотренной выше цепи приведен в численном примере.