В последовательное соединение в цепях переменного тока кроме резисторов могут входить реактивные элементы - индуктивности и емкости, а также источники ЭДС (рис. 1 а).
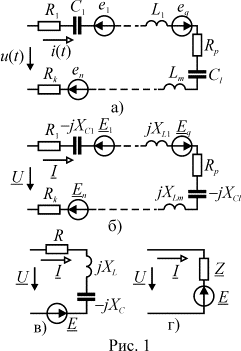 Преобразуем
цепь, представив ее элементы комплексными
сопротивлениями (рис. 1 б), и запишем для контура уравнение по второму
закону Кирхгофа
Преобразуем
цепь, представив ее элементы комплексными
сопротивлениями (рис. 1 б), и запишем для контура уравнение по второму
закону Кирхгофа
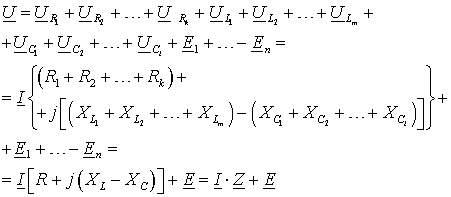
Таким образом, в последовательном соединении все резистивные,
индуктивные и емкостные сопротивления можно заменить эквивалентными суммами 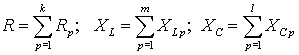 , а источники ЭДС – эквивалентным источником, с ЭДС равной
алгебраической сумме
, а источники ЭДС – эквивалентным источником, с ЭДС равной
алгебраической сумме  , где положительный знак соответствует ЭДС, направление
которых встречно по отношению к направлению тока в соединении
, где положительный знак соответствует ЭДС, направление
которых встречно по отношению к направлению тока в соединении ![]() .
.
Объединяя активное и реактивные сопротивления в комплексное сопротивление ![]() , где
, где ![]() , окончательно получим, что последовательное соединение
, окончательно получим, что последовательное соединение ![]() ,
, ![]() ,
, ![]() и источников ЭДС
и источников ЭДС ![]() , можно заменить последовательным соединением эквивалентного
комплексного сопротивления
, можно заменить последовательным соединением эквивалентного
комплексного сопротивления ![]() и источника ЭДС
и источника ЭДС ![]() (рис. 1 г).
(рис. 1 г).
Из выражений для эквивалентных комплексных реактивных сопротивлений можно
исключить угловую частоту ![]() . Тогда мы получим выражения для эквивалентных параметров
последовательного соединения –
. Тогда мы получим выражения для эквивалентных параметров
последовательного соединения –
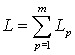 и
и 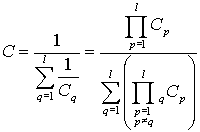 .
.
Мнимая часть комплексного сопротивления ![]() может быть
положительной или отрицательной в зависимости от того, какое сопротивление
больше, индуктивное
может быть
положительной или отрицательной в зависимости от того, какое сопротивление
больше, индуктивное ![]() или емкостное
или емкостное ![]() . Соответственно и сдвиг фаз между током и напряжением в этой
цепи может изменяться в пределах
. Соответственно и сдвиг фаз между током и напряжением в этой
цепи может изменяться в пределах ![]() .
.
Следует заметить, что при наличии в цепи реактивных элементов обоих типов
(индуктивности и емкости) в эквивалентной цепи один или оба реактивных элемента
будут отсутствовать. Если ![]() , то в эквивалентной цепи не будет емкости. В противном
случае будет отсутствовать индуктивность. При равенстве
, то в эквивалентной цепи не будет емкости. В противном
случае будет отсутствовать индуктивность. При равенстве ![]() в эквивалентной цепи
вообще не будет реактивных элементов.
в эквивалентной цепи
вообще не будет реактивных элементов.
При отсутствии каких-либо элементов в исходной схеме, например резисторов или источников ЭДС, будут отсутствовать и соответствующие компоненты эквивалентного представления.
 В
параллельное соединение (рис. 2) могут входить резистивные и реактивные
элементы, а также источники тока.
В
параллельное соединение (рис. 2) могут входить резистивные и реактивные
элементы, а также источники тока.
Источники ЭДС не могут соединяться параллельно, т.к., если два источника ![]() и
и ![]() подключены к узлам
соединения, то
подключены к узлам
соединения, то ![]() и
и ![]() , что возможно только при
, что возможно только при ![]() .
.
В соответствии с первым законом Кирхгофа общий ток, протекающий через соединение в целом, можно представить в виде суммы токов, протекающих через отдельные элементы
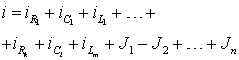
Перейдем к изображениям токов, представив элементы цепи их комплексными проводимостями (рис. б)
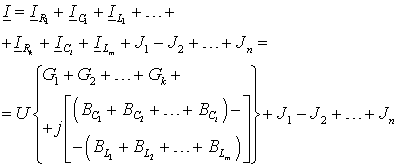
Таким образом, в параллельном соединении все резистивные, индуктивные и емкостные
проводимости можно заменить эквивалентными суммами 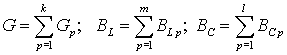 , а источники тока – эквивалентным источником, ток которого равен
алгебраической сумме
, а источники тока – эквивалентным источником, ток которого равен
алгебраической сумме  , где положительный знак соответствует ЭДС, направление
которых встречно направлению тока
, где положительный знак соответствует ЭДС, направление
которых встречно направлению тока ![]() относительно узла соединения.
относительно узла соединения.
Объединяя активную и реактивные проводимости в комплексную проводимость ![]() , где
, где ![]() , окончательно получим, что параллельное соединение
, окончательно получим, что параллельное соединение ![]() ,
, ![]() ,
, ![]() и источников тока
и источников тока ![]() , можно заменить параллельным соединением эквивалентного
комплексной проводимости
, можно заменить параллельным соединением эквивалентного
комплексной проводимости ![]() и источника тока
и источника тока ![]() (рис. 2 г).
(рис. 2 г).
Из выражений для эквивалентных комплексных реактивных проводимостей можно
исключить угловую частоту ![]() . Тогда мы получим выражения для эквивалентных параметров параллельного
соединения –
. Тогда мы получим выражения для эквивалентных параметров параллельного
соединения –
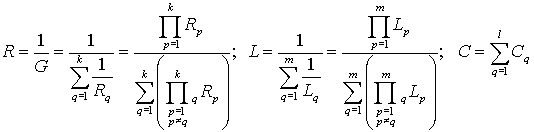 .
.
Из этих выражений следует, что параллельное подключение резистора или индуктивности уменьшает их эквивалентные значения, а параллельное подключение емкости - увеличивает эквивалентную емкость.
Мнимая часть комплексной проводимости ![]() может быть
положительной или отрицательной в зависимости от того, какая проводимость
больше, емкостная
может быть
положительной или отрицательной в зависимости от того, какая проводимость
больше, емкостная ![]() или индуктивная
или индуктивная ![]() . Соответственно и сдвиг фаз между током и напряжением в этой
цепи может изменяться в пределах
. Соответственно и сдвиг фаз между током и напряжением в этой
цепи может изменяться в пределах ![]() .
.
Примечание:
отрицательный знак в выражении для ![]() связан с тем, что
этот угол в соответствии с законом Ома отсчитывается от напряжения.
связан с тем, что
этот угол в соответствии с законом Ома отсчитывается от напряжения.
Также как в последовательном соединении, при наличии в цепи реактивных
элементов обоих типов (индуктивности и емкости) в эквивалентной цепи один или
оба реактивных элемента будут отсутствовать. Если ![]() , то в эквивалентной цепи не будет емкости. В противном
случае будет отсутствовать индуктивность. При равенстве
, то в эквивалентной цепи не будет емкости. В противном
случае будет отсутствовать индуктивность. При равенстве ![]() в эквивалентной цепи
вообще не будет реактивных элементов.
в эквивалентной цепи
вообще не будет реактивных элементов.
При отсутствии каких-либо элементов в исходной схеме, например резисторов или источников тока, будут отсутствовать и соответствующие компоненты эквивалентного представления.
Эквивалентная цепь рис. 2 г представляет собой источник электрической энергии с внутренним источником тока. Очевидно, что ее можно преобразовать в эквивалентный источник с внутренним источником ЭДС (рис. 2 д).
Для цепи рис. 2 г справедливо ![]() , а для цепи рис. 2.д –
, а для цепи рис. 2.д – 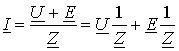 . Вычитая из одного выражения другое, получим условие
преобразования эквивалентных источников
. Вычитая из одного выражения другое, получим условие
преобразования эквивалентных источников
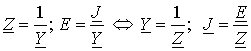 .
.
Таким образом, после преобразования эквивалентная цепь параллельного соединения будет идентична эквивалентной цепи последовательного соединения.
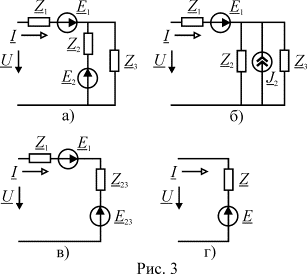 Рассмотрим
теперь общий случай смешанного соединения ветвей электрической цепи.
Рассмотрим
теперь общий случай смешанного соединения ветвей электрической цепи.
Любая ветвь по определению не
содержит узлов и образует последовательное соединение
элементов, которое всегда может быть представлено эквивалентным соединением комплексного
сопротивления ![]() и источника ЭДС
и источника ЭДС ![]() или только
сопротивления. На рис.3 а показана ветвь 1 (
или только
сопротивления. На рис.3 а показана ветвь 1 (![]() ) и последовательно с ней параллельное соединение ветвей 2 (
) и последовательно с ней параллельное соединение ветвей 2 (![]() ) и 3 (
) и 3 (![]() ).
).
Ветвь 2 с помощью эквивалентного преобразования может быть
представлена параллельным соединением ![]() (рис. 3 б), где
(рис. 3 б), где ![]() , а затем параллельное соединение
, а затем параллельное соединение ![]() – последовательным
– последовательным ![]() , где
, где 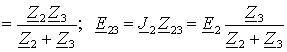 .
.
Полученное последовательное соединение (рис. 3 в) окончательно
преобразуется в источник ЭДС ![]() и комплексное
сопротивление
и комплексное
сопротивление ![]() (рис. 3 г)
(рис. 3 г)