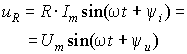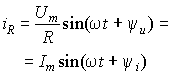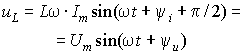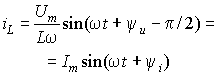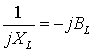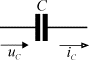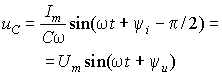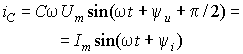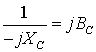Для электрической цепи переменного тока справедливы все соотношения и параметры установленные ранее, исходя из энергетических преобразований. Поэтому для получения основных зависимостей на переменном токе достаточно в эти выражения ввести соответствующие величины.
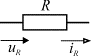
Пусть напряжение в цепи с сопротивлением ![]() изменяется по закону
изменяется по закону ![]() . Тогда в соответствии с таблицей 1 ток в
ней будет
. Тогда в соответствии с таблицей 1 ток в
ней будет
![]() (1)
(1)
 Отсюда следует, что начальные фазы тока и напряжения на этом
участке одинаковы
Отсюда следует, что начальные фазы тока и напряжения на этом
участке одинаковы ![]() , а амплитуда тока равна
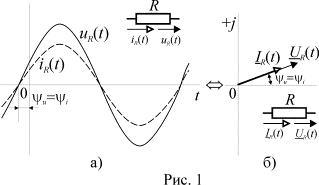
, а амплитуда тока равна ![]() . Временные диаграммы, соответствующие этим отношениям
приведены на рис. 1 а). Там же показано изображение сопротивления на электрических
схемах с условно положительными направлениями тока и напряжения.
. Временные диаграммы, соответствующие этим отношениям
приведены на рис. 1 а). Там же показано изображение сопротивления на электрических
схемах с условно положительными направлениями тока и напряжения.
Амплитудные и действующие
значения синусоидальных величин связаны между собой постоянным коэффициентом,
поэтому, разделив на ![]() выражение для
амплитуды тока получим соотношение действующих значений тока и напряжения на
сопротивлении
выражение для
амплитуды тока получим соотношение действующих значений тока и напряжения на
сопротивлении ![]() или
или ![]() .
.
Синусоидальные функции выражения (1) можно представить их изображениями в виде векторов и соответствующих им комплексных чисел
и изобразить их на векторной диаграмме (рис. 1 б).
В электрических цепях с синусоидальными переменными токами и напряжениями помимо статических явлений, свойственных цепям постоянного тока, появляются динамические эффекты, т.е. эффекты связанные с изменением этих величин во времени.
Так на любом участке электрической цепи, по которому протекает переменный
ток ![]() будет действовать ЭДС самоиндукции
будет действовать ЭДС самоиндукции ![]() , наводимая изменяющимся во времени магнитным потоком, и
равное ей, но направленное в противоположную сторону падение напряжения
, наводимая изменяющимся во времени магнитным потоком, и
равное ей, но направленное в противоположную сторону падение напряжения ![]()
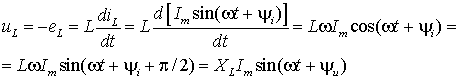 (3)
(3)
 Величина
Величина ![]() , имеет размерность сопротивления и называется индуктивным
сопротивлением. Амплитуда напряжения, возникающего за счет ЭДС
самоиндукции, равна
, имеет размерность сопротивления и называется индуктивным
сопротивлением. Амплитуда напряжения, возникающего за счет ЭДС
самоиндукции, равна ![]() , а начальная фаза
, а начальная фаза ![]() больше начальной фазы
протекающего тока на
больше начальной фазы
протекающего тока на ![]() , т.е. напряжение опережает по фазе ток на
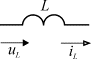
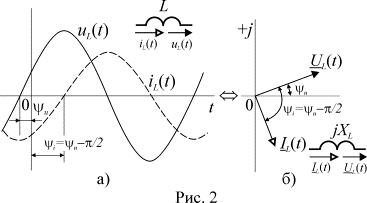
, т.е. напряжение опережает по фазе ток на ![]() . Временные диаграммы, соответствующие выражению (3),
приведены на рис. 2 а.
. Временные диаграммы, соответствующие выражению (3),
приведены на рис. 2 а.
Из выражения для амплитуды падения напряжения на индуктивности можно
определить его действующее значение ![]() или действующее
значение тока
или действующее
значение тока ![]() , где величина
, где величина ![]() называется индуктивной
проводимостью.
называется индуктивной
проводимостью.
Индуктивное сопротивление по сути своей является распределенным параметром, т.к. магнитный поток существует везде, где протекает электрический ток, и на всех участках электрической цепи будет наводиться ЭДС самоиндукции, пропорциональная соответствующему индуктивному сопротивлению. Однако на практике индуктивность всей цепи или отдельного участка считают сосредоточенной в отдельном элементе, изображаемом на схемах в виде рис. 2 а.
Пользуясь таблицей 2, выражение (3) можно представить векторами в комплексной форме в виде:
где ![]() - комплексное
индуктивное сопротивление.
- комплексное
индуктивное сопротивление.
Векторная диаграмма и схема замещения для выражения (2) приведены на рис. 2 б.
Из выражения (4) можно определить комплексное значение тока через падение напряжения
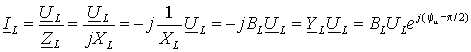
где ![]() - комплексная
индуктивная проводимость.
- комплексная
индуктивная проводимость.
Пусть напряжение на емкости изменяется во времени по синусоидальному закону ![]() . Тогда из таблицы 1 ток в
емкости определится в виде
. Тогда из таблицы 1 ток в
емкости определится в виде
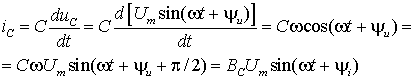 (5)
(5)
Произведение ![]() имеет размерность
проводимости [1/Ом=См] и называется
емкостной проводимостью. Отсюда амплитуда тока равна
имеет размерность
проводимости [1/Ом=См] и называется
емкостной проводимостью. Отсюда амплитуда тока равна ![]() , а начальная фаза –
, а начальная фаза – ![]() . Таким образом, ток в емкости опережает падение
напряжения на ней на
. Таким образом, ток в емкости опережает падение
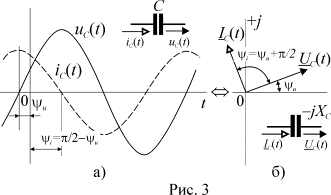
напряжения на ней на ![]() . Временные диаграммы, соответствующие этим соотношениям
тока и напряжения на емкости приведены на рис. 3 а.
. Временные диаграммы, соответствующие этим соотношениям
тока и напряжения на емкости приведены на рис. 3 а.
 Пользуясь связью между амплитудными и действующими значениями, для
тока и падения напряжения на емкости можно записать
Пользуясь связью между амплитудными и действующими значениями, для
тока и падения напряжения на емкости можно записать ![]() или
или ![]() , где величина
, где величина 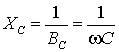 называется емкостным
сопротивлением.
называется емкостным
сопротивлением.
Из выражения (5) следует, что всякое изменение потенциалов в электрической цепи будет вызывать появление токов, приводящих к перераспределению зарядов. Причем, под токами в этом процессе следует понимать как токи проводимости, так и токи смещения, возникающие между всеми участках цепи. Поэтому емкостная проводимость, как и емкость, является распределенным параметром, но для расчетов ее, аналогично индуктивности, представляют сосредоточенной в отдельном элементе, который изображается на схеме в виде рис. 3 а.
Связь между напряжением и током в емкости можно представить также векторами (рис. 3 б) и соответствующими комплексными числами в виде
где ![]() - комплексная
емкостная проводимость.
- комплексная
емкостная проводимость.
Отсюда можно также определить комплексное падение напряжения на емкости
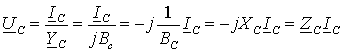
где ![]() - комплексное
емкостное сопротивление.
- комплексное
емкостное сопротивление.
Индуктивность L и емкость C называются реактивными элементами электрической цепи. Реактивными называются также соответствующие сопротивления и проводимости. Это связано с тем, что падение напряжения на индуктивности и ток через емкость появляются только как следствие или реакция на изменение тока или разности потенциалов.
В резисторе падение напряжения не связано с изменением тока, поэтому его сопротивление, в отличие от реактивного, называется активным или резистивным сопротивлением.
Сведем полученные выше результаты в таблицу.
|
Элемент цепи |
Оригиналы функций |
Изображения функций |
||||
|
Напряжение |
Ток |
Комплексное
сопротивление |
Комплексная проводимость |
Напряжение |
Ток |
|
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|||