Принцип наложения и основанный на нем метод расчета является следствием понятия линейной электрической цепи. Для такой цепи уравнения Кирхгофа образуют линейную систему алгебраических уравнений, которая в матричной форме записи имеет вид

.

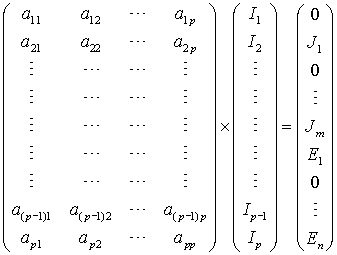Вектор свободных членов этой системы состоит из нулей, токов и ЭДС источников электрической энергии. Причем, под и будем понимать алгебраическую сумму токов и ЭДС источников объединенных в -м узле и -м контуре электрической цепи, т.е. 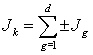и .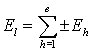

Общее решение этой системы уравнений для -го тока может быть найдено по формуле Крамера в виде

, (1)

где некий безразмерный коэффициент, а – коэффициент, имеющий размерность проводимости. Если в -м узле и -м контуре цепи объединяются несколько источников, то соответствующее слагаемое в правой части решения распадается на алгебраическую сумму слагаемых с одинаковыми коэффициентами и .

Таким образом, каждое слагаемое в правой части решения (1) соответствует составляющей -го тока, создаваемой каким-либо одним источником электрической энергии при отсутствии остальных источников. Поэтому решение для любого тока в электрической цепи можно найти в виде суммы частных решений, полученных при воздействии на цепь каждого действующего в ней источника в отдельности.

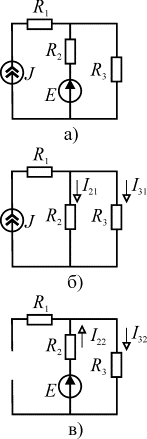Рассмотрим применение метода наложения на примере определения тока в электрической цепи приведенной на рис а.

В этой цепи два источника электрической энергии, поэтому искомый ток определится в виде суммы двух частичных токов.

Исключим вначале источник ЭДС в цепи, заменив его внутренним сопротивлением (). В результате цепь преобразуется к виду, показанному на рис. б.

Ток , создаваемый источником, разветвляется на два тока и . По закону Ома с учетом параллельного соединения и

.

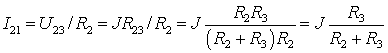Исключим теперь источник тока (рис. в). Ветвь с будет иметь бесконечно большое сопротивление и ток в ней будет равен нулю. Поэтому второй частичный ток определится по закону Ома для контура –

.

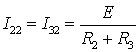Полный ток в с учетом того, что частичные токи протекают в различных направлениях, будет равен

.

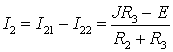Истинное направление тока зависит от соотношения величин в числителе этого выражения. Если он положителен, то направление полного тока соответствует направлению .