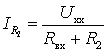 Метод
эквивалентного генератора используется для расчета электрических цепей в том
случае, если требуется найти напряжение или ток в каком-либо одном сопротивлении.
В этом случае вся электрическая цепь, кроме этого сопротивления заменяется эквивалентным
источником электрической энергии (генератором), а затем искомая величина
определяется по закону Ома.
Метод
эквивалентного генератора используется для расчета электрических цепей в том
случае, если требуется найти напряжение или ток в каком-либо одном сопротивлении.
В этом случае вся электрическая цепь, кроме этого сопротивления заменяется эквивалентным
источником электрической энергии (генератором), а затем искомая величина
определяется по закону Ома.
Возможность замены любой электрической цепи эквивалентным генератором можно доказать следующими рассуждениями.
Пусть требуется определить ток ![]() в некотором сопротивлении
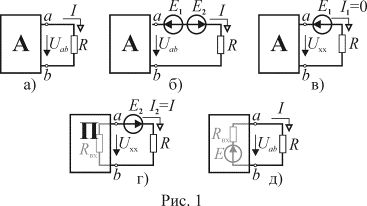
в некотором сопротивлении ![]() . Всю электрическую цепь, кроме этого сопротивления можно
представить активным двухполюсником (А рис.1), т.е. двухполюсником
содержащим кроме сопротивлений источники электрической энергии.
. Всю электрическую цепь, кроме этого сопротивления можно
представить активным двухполюсником (А рис.1), т.е. двухполюсником
содержащим кроме сопротивлений источники электрической энергии.
Включим последовательно с сопротивлением ![]() два одинаковых источника ЭДС (
два одинаковых источника ЭДС (![]() ), соединенных встречно (рис. 1 б). Так как их внутреннее
сопротивление равно нулю, а встречные ЭДС компенсируют друг друга, то подключение
не вызовет изменения режима электрической цепи.
), соединенных встречно (рис. 1 б). Так как их внутреннее
сопротивление равно нулю, а встречные ЭДС компенсируют друг друга, то подключение
не вызовет изменения режима электрической цепи.
Отключим источник ![]() , а величину ЭДС
, а величину ЭДС ![]() подберем таким
образом, чтобы ток
подберем таким
образом, чтобы ток ![]() в сопротивлении
в сопротивлении ![]() в этом режиме работы
цепи стал равным нулю (рис. 1 в). При этом ЭДС
в этом режиме работы
цепи стал равным нулю (рис. 1 в). При этом ЭДС ![]() будет полностью
компенсировать напряжение, создаваемое двухполюсником А при отсутствии тока на
его выходе
будет полностью
компенсировать напряжение, создаваемое двухполюсником А при отсутствии тока на
его выходе ![]() , т.е. в режиме холостого хода. Соответственно этому
, т.е. в режиме холостого хода. Соответственно этому ![]() .
.
Подключим теперь источник ![]() и одновременно
отключим все остальные источники электрической энергии. В этом случае
двухполюсник будет пассивным (П на рис. 1 г) и всегда может быть представлен эквивалентным
или входным сопротивлением
и одновременно
отключим все остальные источники электрической энергии. В этом случае
двухполюсник будет пассивным (П на рис. 1 г) и всегда может быть представлен эквивалентным
или входным сопротивлением ![]() . При этом в сопротивлении
. При этом в сопротивлении ![]() будет протекать ток
будет протекать ток 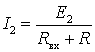 (рис. 1 г).
(рис. 1 г).
Если теперь, пользуясь принципом наложения (суперпозиции), представить
искомый ток в ![]() в виде суммы токов,
создаваемых в двух рассмотренных выше режимах, то, с учетом установленных ранее
соотношений, он окажется равным
в виде суммы токов,
создаваемых в двух рассмотренных выше режимах, то, с учетом установленных ранее
соотношений, он окажется равным
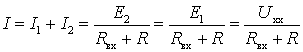 .
.
Таким образом, всю электрическую цепь по отношению к любому сопротивлению
![]() можно заменить эквивалентным
генератором (рис. 1 д), ЭДС которого
можно заменить эквивалентным
генератором (рис. 1 д), ЭДС которого ![]() равна напряжению в
точках подключения
равна напряжению в
точках подключения ![]() в режиме холостого
хода, а внутреннее (входное) сопротивление – эквивалентному сопротивлению цепи
относительно этих точек.
в режиме холостого
хода, а внутреннее (входное) сопротивление – эквивалентному сопротивлению цепи
относительно этих точек.
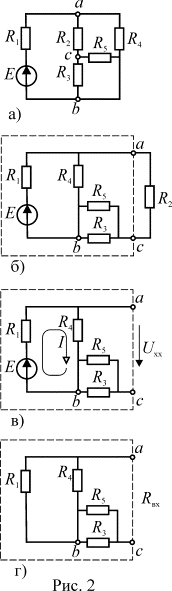 Рассмотрим
применение этого метода к задаче определения тока в сопротивлении
Рассмотрим
применение этого метода к задаче определения тока в сопротивлении ![]() на рис. 2 а.
на рис. 2 а.
Изобразим исходную цепь, выделив в ней ![]() так, как это показано
на рис.2 б.
так, как это показано
на рис.2 б.
Найдем теперь напряжение между точками ![]() в режиме холостого
хода.
в режиме холостого
хода.
При отсутствии сопротивления ![]() ток в цепи
ток в цепи ![]() будет замыкаться по
контуру
будет замыкаться по
контуру ![]() (рис. 2. в) и
напряжение
(рис. 2. в) и
напряжение ![]() будет равно падению
напряжения на
будет равно падению
напряжения на ![]() , т.к. в параллельном соединении
, т.к. в параллельном соединении ![]() ток отсутствует и
падение напряжения на нем равно нулю. Поэтому по закону Ома
ток отсутствует и
падение напряжения на нем равно нулю. Поэтому по закону Ома
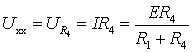 .
.
Схему для определения входного сопротивления цепи (рис. 2 г)
получим, заменив источник ЭДС ![]() его внутренним
сопротивлением (
его внутренним
сопротивлением (![]() ). Она представляет собой последовательное соединение двух
пар параллельных соединений –
). Она представляет собой последовательное соединение двух
пар параллельных соединений – ![]() и
и ![]() . Отсюда
. Отсюда
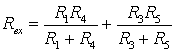 .
.
Теперь ток в ![]() можно найти как
можно найти как