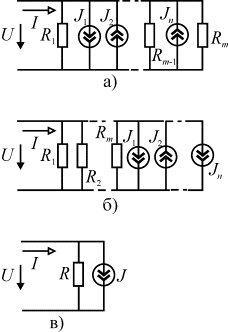
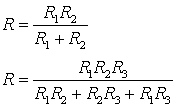В любое параллельное соединение может входить произвольное число сопротивлений (резисторов) и источников тока, а также не более одного источника ЭДС. Наличие более одного источника ЭДС в соединении исключается вследствие логического противоречия, т.к. в параллельном соединении на всех все элементах одинаковое падение напряжения и оно равно ЭДС источника. Если же источников ЭДС несколько, то они должны формировать несколько различных ЭДС, что невозможно по характеру соединения. Присутствие источника ЭДС в соединении означает лишь то, что падение напряжения в соединении задано, поэтому без ущерба для общности выводов источник ЭДС можно вынести за пределы соединения и не рассматривать. Тогда в общем случае в соединение будут входить сопротивлений и источников тока (рис а). Не изменяя режима работы соединения, их можно переместить так, чтобы образовались две группы элементов: сопротивления и источники тока (рис. б). Для этой цепи можно написать уравнение Кирхгофа в виде:

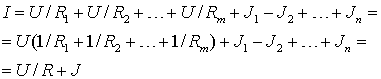
Таким образом, любое параллельное соединение элементов можно представить параллельным соединением одного сопротивления и одного источника тока . Причем, общее сопротивление соединения определяется через сумму проводимостей, входящих в множитель – 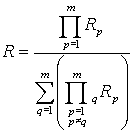, а общий ток источника равен алгебраической сумме 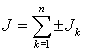, где положительный знак имеют токи, направления которых по отношению к узлу соединения противоположны направлению тока в соединении .

Для наиболее часто встречающихся соединений двух и трех сопротивлений выражения для общего сопротивления имеют вид –