2.3.2.3 Пространственно-векторная модуляция
Метод пространственно-векторной модуляции (ПВМ) был
разработан в середине 90-х годов в связи расширением возможностей систем
микропроцессорного управления. Традиционные методы ШИМ основаны на сравнении
сигнала задания с сигналом линейной развертки (пилообразным напряжением) в
результате чего в обмотках АД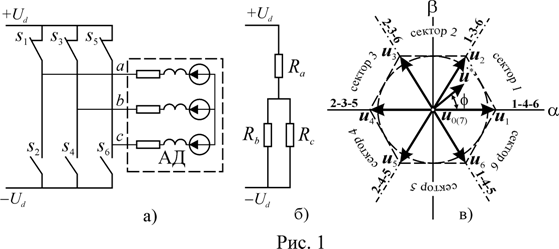 
формировалась последовательность прямоугольных
импульсов, скважность которых изменялась в соответствии с сигналом задания.
Однако из-за влияния электромагнитных процессов (прежде всего ЭДС вращения)
характер изменения токов в обмотках не имеет однозначной связи с законом
изменения сигнала управления и сильно зависит от режима работы АД.
Алгоритм управления ключами автономного инвертора (И)
в режиме ПВМ основан на формировании на каждом временном интервале требуемого
положения вектора напряжения в пространстве. В случае аналогового источника
питания для решения этой задачи достаточно сформировать в каждой обмотке
напряжение, соответствующее проекции заданного вектора на ось обмотки. В
импульсном источнике питания, к которым относится автономный инвертор (рис. 1
а), возможно формирование только восьми состояний (положений) вектора
напряжения (рис. 1 в), включая два нулевых, формируемых инвертором при
замыкании нечетных (
) и четных (
) ключей. Эти векторы
называют базовыми векторами.
Модуль ненулевого базового вектора можно определить,
пользуясь понятием обобщенного вектора. Пусть задано какое-либо замкнутое
состояние ключей, например, 1-4-6. Тогда обмотки статора будут подключены к
источнику постоянного тока по схеме рис. 1 б). В силу симметрии обмоток и с
учетом направления (в 
от начала к концу, в 
и 
от конца к началу)
напряжения на них составят – 
. Отсюда модуль вектора напряжения или
базового вектора равен
.
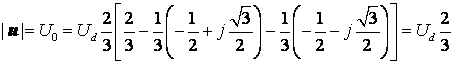Очевидно, что для всех других состояний ключей мы получим тот же результат.
Формирование вектора с заданным
средним значениям модуля и пространственного угла производится поочередным
формированием базовых векторов, образующих границы сектора, в котором находится
результирующий вектор, и нулевого вектора.
Определим длительность этих интервалов, полагая, что модули
граничных векторов равны средним значениям. Пусть требуется сформировать вектор
рис. 1 в). Он находится в первом секторе, ограниченном базовыми
векторами 
и 
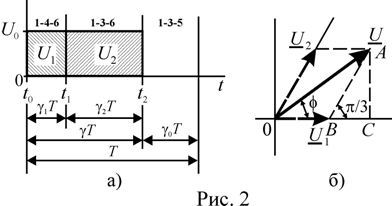
. На первом интервале (
рис. 2 а)
формируется вектор (ключи 1-4-6), на втором (
) – вектор
(ключи
1-3-6). И, наконец, замыкаются ключи 1-3-5 и формируется короткое замыкание
статора АД. Тогда средние значения граничных векторов равны
(1)
где 
– относительные длительности
коммутации при заданном модуле результирующего вектора 
с относительным
значением 
; 
– относительные
длительности коммутации при заданном модуле базового вектора 
.
Результирующий пространственный вектор равен геометрической сумме граничных
векторов со средними модулями 
и 
. Из прямоугольного
треугольника 
рис. 2 б), найдем их модули
(2)
Тогда из выражений (1) и (2) относительные длительности коммутации будут равны
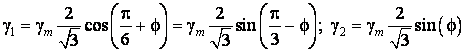(3)
Зная относительные
длительности коммутации можно найти относительную длительность паузы как 
, где 
(4)
– суммарная относительная длительность формирования
ненулевых векторов. На границах сектора (
) относительная длительность 
принимает
значение относительного модуля результирующего вектора 
, а при 
и 
косинусная
функция 
(рис.
3 а) имеет максимум, равный 
, что в принципе невозможно, т.к. 
.
Следовательно, при у функции появится линейный
участок 
(рис.
3 а), отграниченный условием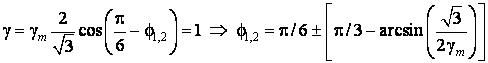 
.
Определим теперь модуль результирующего вектора через
относительные длительности (3). Из треугольника рис.2 б)
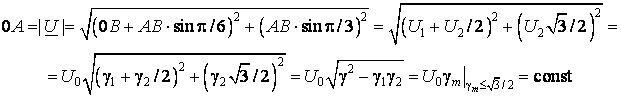
Таким образом, при принятых условиях формирования
результирующего вектора, его модуль не зависит от аргумента 
(рис. 3 б), а
годограф представляет собой окружность (рис. 3. в).
Максимальный модуль любого вектора напряжения равен
модулю базового вектора 
. Поэтому максимальный радиус
кругового годографа результирующего вектора будет равен 
(рис. 3. в).
Рассмотрим теперь случай 
. Тогда 
и из (4) модуль
результирующего вектора будет равен
. (5)
Отсюда следует, что модуль вектора изменяется при
изменении (рис. 3. б), достигая величины
базового вектора на границах сектора и уменьшаясь до
значения 
в середине. Подставив (5) в выражение
(2) для 
,
с учетом получим
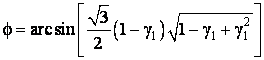(6)
Выражениям (5-6) соответствует годограф результирующего вектора в виде прямой линии, соединяющей концы базовых векторов.
Таким образом, при относительном модуле 
результирующий
вектор может иметь круговой годограф (рис. 3. в). При
годограф
становится шестиугольником, образованным отрезками прямых, соединяющих концы
базовых векторов, а для промежуточных значений относительного модуля 
сектор
базовых векторов разбивается на три сектора. Для углов 
годограф
результирующего вектора линеен, а при 
и 
может быть окружностью.
Проектируя результирующий вектор на фазные оси, мы
получим для круговых годографов с модулем синусоидальные средние
фазные напряжения (рис. 3 г). В предельном случае эти
напряжения будут представлять собой кривую, показанную на рис. 3 г). Она
совпадает с синусоидой в точках 
(
) и отклоняется на +13,4% и
+6,7% соответственно в точках 
.
В случае необходимости формирования кругового
годографа результирующего вектора с заданным значением плоскость базовых
векторов разбивают на секторы, число которых 
кратно шести. Это число
определяет шаг формирования или количество результирующих векторов, что в свою
очередь определяет гармонический состав выходного напряжения.
Для каждого из 
секторов по выражениям (3) при 
определяют
относительные длительности интервалов (
), а затем с помощью линейной
развертки аналогичной развертке ШИМ формируют временные интервалы и
осуществляют коммутацию по какому-либо алгоритму.
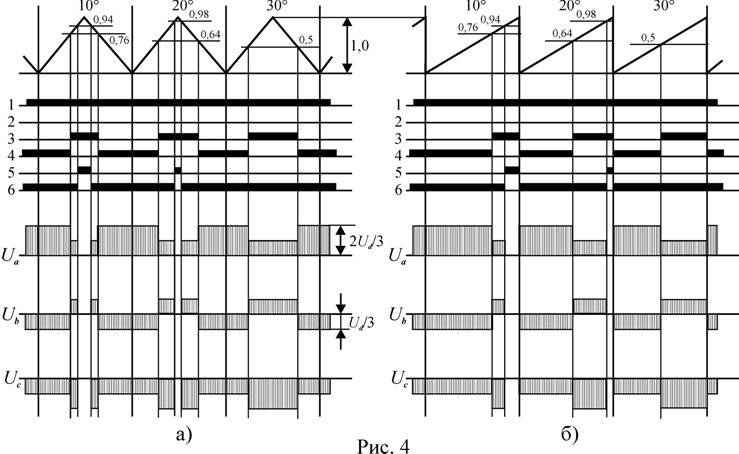
На рисунке 4 показан один из возможных алгоритмов
работы с симметричным и несимметричным сигналом развертки 
при 
и 
. В этом
случае в пределах каждого сектора базовых векторов будет формироваться шесть
результирующих с интервалом в 10°. В интервалах 
формируется
начальный базовый вектор сектора (на рис. 4 ); при 
– конечный базовый
вектор (на рис. 4 ) и при 
– нулевой вектор 
. На
рисунке показаны расчетные уровни сигналов, состояния ключей инвертора (рис. 1 а) и выходные фазные напряжения для 
ными словами процесс модуляции разделяется на три временных интервала. В первом интервале замыкаются ключи, соответствующие состоянию вектора начальной границы сектора; во втором – вектору конечной границы сектора и в третьем замыкаются либо все нечетные, либо все четные ключи, формируя нулевой вектор.
Современные инверторы работают при частотах коммутации 18¼20 кГц, что позволяет формировать методом ПВМ в обмотках статора АД напряжения с практически синусоидально изменяющимся средним значением.