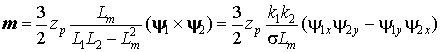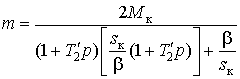Основой для анализа динамических свойств АД могут служить векторные уравнения статора и ротора в синхронной системе координат

1.2.3 Динамические характеристики АД при питании от источника напряжения

(1)

и уравнение электромагнитного момента, представленное через потокосцепления статора и ротора

, (2)

где – соответственно, коэффициенты электромагнитной связи статора и ротора и коэффициент рассеяния.

Представим токи статора и ротора через потокосцепления 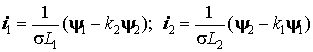и, подставив в уравнения (1), запишем их в форме Коши

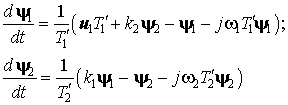(3)

где и – переходные постоянные времени статора и ротора, т.е. постоянные времени, соответствующие переходным индуктивностям и (рис. 1).

Совместим вектор напряжения статора с осью системы координат (). Тогда, разделяя проекции векторов, получим

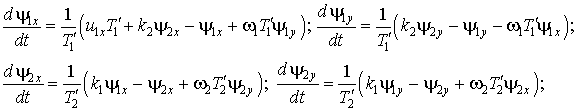(4)

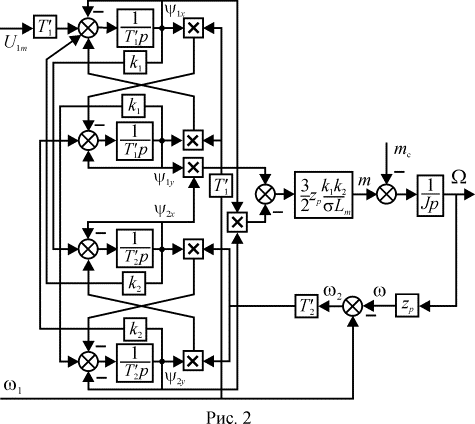Уравнения (2-4) можно представить в виде структурной схемы, показанной на рисунке 2. Она имеет два входа, соответствующих управляющим воздействиям по напряжению и частоте статора. Принципиально можно ограничится воздействием на АД только по одному из входов, установив на другом заданное постоянное значение величины. В этом случае мы получим управление двигателем с помощью изменения напряжения питания или частоты статора. Однако управление изменением напряжения при глубоком регулировании обладает крайне низкими энергетическими показателями и в современном приводе применяется крайне редко для машин малой мощности. Управление изменением частоты при постоянном напряжении питания применяется только для регулирования скорости вращения вверх от номинальной. При этом магнитный поток АД уменьшается обратно пропорционально повышению частоты и двигатель работает в режиме постоянной располагаемой мощности. Чаще всего для обеспечения оптимальных условий протекания процессов преобразования энергии в АД между входами управления устанавливают

При питании от источника напряжения () потокосцепление статора изменяется незначительно, в основном из-за падения напряжения на активном сопротивлении , т.е. . Если принять , то можно считать и тогда из уравнения статора следует

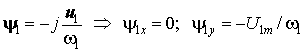(5)

Заменив производную в уравнении ротора (1) оператором Лапласа и разделяя проекции векторов, получим

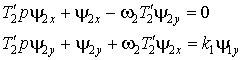. (6)

Отсюда . Подставляя это выражение во второе уравнение, определим искомое значение

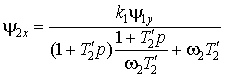. (7)

В этом выражении дальнейшие алгебраические преобразования невозможны, т.к. первый оператор дифференцирования в знаменателе относится ко всей дроби , где в общем случае является функцией времени.

Заметим, что ,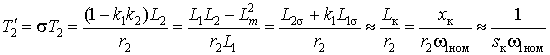

где: – индуктивность короткого замыкания, а – приближенное значение критического скольжения. Если произведение представить как , где 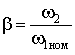– относительная частота ротора или абсолютное скольжение, то из (7) мы получим

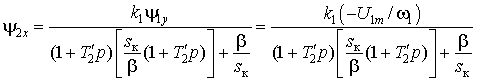. (8)

После чего из (5) с учетом (8) можно получить уравнение динамической механической характеристики

, (9)

где .

По выражениям (6) и (9) можно построить структурную схему (рис. 3). Она соответствует АД, управляемому напряжением и частотой статора при условии или, что то же самое, .

Уравнение (9) отражает влияние электромагнитной инерции на электромеханические процессы в АД. Оно нелинейно, но для малых приращений на рабочем участке механической характеристики его можно линеаризовать. Для этого вначале выполним дифференцирование

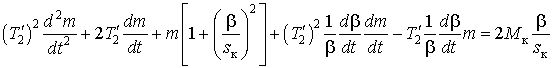а затем разложим полученное уравнение в ряд Тейлора в окрестности точки . Пренебрегая членами ряда высшего порядка, после преобразований представим уравнение механической характеристики в приращениях в виде

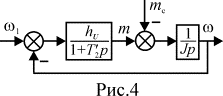Это уравнение позволяет анализировать электромеханические процессы в любой точке статической механической характеристики. Однако для АД наибольший интерес представляет рабочий участок характеристики при . Тогда, полагая и , соответственно и , получим

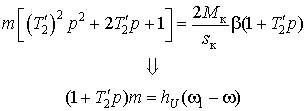
где (9)

– модуль жесткости линеаризованной механической характеристики.

Таким образом, на рабочем участке механической характеристики АД можно представить звеном первого порядка (рис. 4) с передаточной функцией динамической жесткости

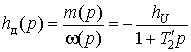(10)

Переходная постоянная времени ротора двигателей общего применения составляет величину 0,05-0,005 с, и меньшие значения соответствуют двигателям малой мощности