Лекция 8

ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

В одном из предыдущих разделов мы рассматривали динамические характеристики механической подсистемы обособленно от электрической части. Управляющим воздействием для нее являлся электромагнитный момент ЭМП, который задавался независимой функцией времени. Переходные процессы в такой подсистеме обуславливались изменением управляющего момента и моментов нагрузок (возмущений) и назывались механическими переходными процессами.

В электромеханической подсистеме электромагнитный момент ЭМП в соответствии с механической характеристикой зависит от механической переменной - скорости. Электромеханическая связь объединяет механическую и электрическую части ЭМП в единую систему, переходные процессы в которой носят название электромеханических переходных процессов.

Электромеханическим переходным процессом называется процесс перехода ЭМС от одного установившегося режима к другому, когда одновременно меняются скорость и электромагнитный момент ЭМП. К переходным процессам относятся в частности процессы пуска, торможения и реверса электродвигателя, процессы, обусловленные изменением задающих и возмущающих воздействий ЭМС.

Здесь мы сосредоточим внимание на характере переходных про-цессов в электромеханической системе “ ЭМП - механизм” с жесткими механическими связями , когда механизм представляется одномассовой моделью. Система уравнений состояния для такой ЭМС нам известна,

dM/dt = -(1/ Tэ)M - (b / Tэ)w 1+ (b / Tэ) w 0,

dw 1/dt= (1/ b Tм) M -(1/ b Tм) Mc

Принимая в качестве вектора состояния вектор

Yт =[ M w 1 ] ,

в качестве вектора управления - двумерный вектор

Uт = [w 0 Mc]

и в качестве выходных переменных - сами переменные состояния , мы получили

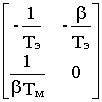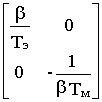A= , B= , C= 1.

Решение ее, определяющее процессы при произвольной форме возмущающих воздействий (элементов вектора управления U), определяется стандартным выражением

Y(t) = e AtY(0) + т e A(t-t ) B U(t ) dt

При анализе реакции ЭМС на скачкообразные изменения управ-ляющего воздействия w0 и момента нагрузки Мс можно считать, что U(t )= const при t і 0 . В этом случае решение принимает вид

Y(t) = e At [ Y(0) - Yпр ] + Yпр ,

где Yпр = -A-1BU- вектор-столбец, определяющий принужденное состояние системы.

Осуществляя обращение матрицы А, получим

A-1= adj A/ det A=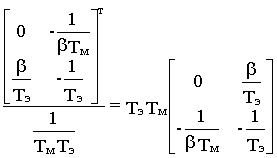

Окончательно

A-1 =

Следовательно,

A-1BU=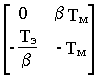 ґ 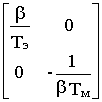ґ =

= ґ =

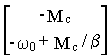
Таким образом

Yпр = -A-1BU= =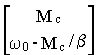

Полученный результат показывает, что

- новый установившийся (или принужденный) режим имеет место при равенстве электромагнитного момента ЭМП и момента нагрузки на валу Мс .

- установившееся (принужденное) значение скорости определяется механической характеристикой системы.

Эти же результаты можно получить из исходной системы уравнений состояния, если приравнять нулю производные переменных состояния (dM/dt и dw 1/dt).

Характер свободной составляющей процесса

Yсв (t)= e At [ Y(0) - Yпр ]

определяется матричной экспонентой e At .

В случае, если собственные числа матрицы А простые - т.е. вещественные и разные, матричная экспонента вычисляется по формуле

Cr e l rt , (8.1)

где матричные коэффициенты Cr могут быть найдены в соответствии с теоремой Кэли-Гамильтона как

Cr =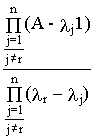 (8.2)

Для системы второго порядка с простыми числами l1 и l2 матричная экспонента может быть найдена в виде

 

e At = +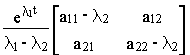

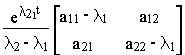
Учитывая, что в нашем случае a11= -1/Тэ, а12= -b /Тэ, а21= 1/b Тм и а22=0, получим

e At = -

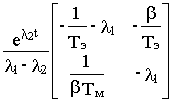
Суммируя матрицы и приводя подобные члены, получим

 e At = 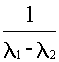ґ

-

 

 

 

 

 

 

Вводя обозначения D M(0) = M(0) - Mпр = M(0) - Mc и Dw(0)=w1(0)- w1пр, найдем свободную составляющую процесса

Yсв (t)= e At [ Y(0) - Yпр ]

Yсв =

+

- +

 

 

 

 

 

 

Прибавляя ранее найденные принужденные составляющие, окончательно получим

M(t)= Mc + +

 

 

(8.3)

w 1(t) = w 1пр - +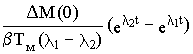

(8.4)

Обратим внимание на то, что

1. реакция системы на скачкообразное изменение управляющего воздействия w0 при постоянном моменте нагрузки Mc на валу ЭМП определяется только первым и третьим слагаемыми выражений 10.1 и 10.2., поскольку M(0)= Mпр и следовательно, DM(0)=0. (причина - электромагнитная инерция, не позволяющая моменту М измениться скачком при скачкообразном изменении управляющего воздействия)

2. при нулевых начальных условиях (w1(0)=0, М(0)=0) , нулевом моменте нагрузки (Мс=0) и единичном значении управляющего воздействия (w0 (0+) из 10.2 получается уже известное нам выражение для переходной характеристики канал w0® w1.

Типовые, апериодические по характеру кривые изменения электромагнитного момента M(t) и скорости w1(t) при скачкообразном возрастании управляющего воздействия w0 и возмущения по моменту нагрузки Мс, соответствующие выражениям 8.1 и 8.2 представлены на рис. 8.1 а, б

 

 

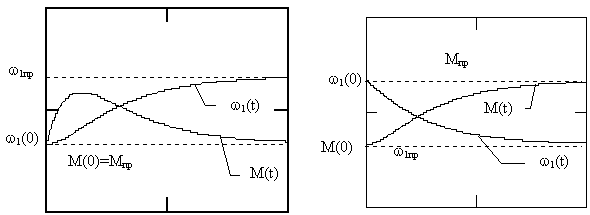
Рис. 8.1, а, б.

Время переходного процесса определяется временем затухания самой “медленной” из экспоненциальных составляющих свободного процесса. В нашем случае кl2п >пl1п и потому время переходного процесса можно определить как tп=3п 1 / l1 п. Отметим, что в переходном режиме могут иметь место всплески электромагнитного момента машины.

В частном случае при Тэ=0 поведение ЭМП будет определяться уравнениями

M =-b w 1+ b w 0,

dw 1/dt= (1/ b Tм) M -(1/ b Tм) Mc

и следовательно,

dw 1/dt= -(1/ Tм) w 1 +(1/ Tм) w 0 -(1/ b Tм) Mc

Учитывая, что w 1пр= w 0 - Mc/b , решение уравнения получим в виде

w 1(t)= w 1пр + [w 1(0) - w 1пр}e -t/Tм (8.5)

Подставляя это выражение в уравнение моментов, получим

M(t) =-b w 1+ b w 0= - b {w 1пр +[w 1(0) - w 1пр]e -t/Tм} +b w 0

Учитывая, что w1пр= w0 - Mc/b , и следовательно b (w0 -w1пр) = Mс, окончательно получим

M(t)=Mc + [M(0+) - Mc}e -t/Tм , где М(0+)=b [w 0(0+)- w 1(0) ] (8.6)

Графики электромеханических процессов при скачкообразных изменениях управляющего и возмущающего воздействий представлены на рисунках 8.2, а и б.

Рис. 8.2, а, б.

С помощью этих рисунков можно пояснить смысл электромеханической постоянной времени обобщенного ЭМТ: Электромеханическая постоянная времени представляет собой время, за которое скорость w1 вала преобразователя достигла бы установившегося значения, двигаясь равномерно ускоренно под действием постоянного динамического момента M(0+). Такое ускорение равно M(0+)/JS .

Анализируя эти процессы, легко установить, что

а) они носят апериодический экспоненциальный характер и время протекания их определяется величиной Тм (tп= 3 Тм)

б) скорость вращения меняется плавно без скачков из-за наличия электромеханической инерции

в) скачкообразное изменение управляющего воздействия приводит к скачкообразному изменению электромагнитного момента из-за отсутствия электромагнитной инерции.

Если среди n собственных чисел матрицы A имеется число ls кратности S, составляющая матричной экспоненты, обусловленная этими числами в общем случае определяется формулой

Cs el st =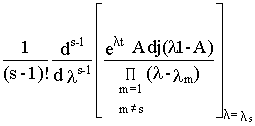 (8.7)

Если все собственные числа матрицы А - вещественные и равные, то выражение 8.3 принимает вид

Cs el st =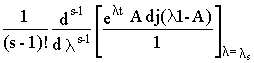 (8.8)

В нашем случае

l 1,2=-d , где d = 1/2 Tэ,

и потому из 8.8 следует. что

e At =

 

 

 

 

Реализуя формулу

Y(t)= e At +

получим

M{t}= +Mс (8.9)

w 1(t)= + +w 1пр (8.10)

Если собственные числа матрицы А - комплексно-сопряженные, т.е.

l 1,2=-d ± jW св, где W св=Ц W 02- d 2, d = 1/2 Tэ и W 0=Ц 1/TмTэ,

матричная экспонента для системы второго порядка, в общем случае определяемая выражениями 8.1 и 8.2, приводится к виду

e At = [(d 1+A)SinW свt+1 W св CosW свt]

Следовательно, для рассматриваемой системы

e At = ґ

 

 

 

Реализуя формулу

Y(t)= e At +

получим

M{t}= 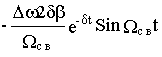+Mс(8.11)

w 1(t)= + +w 1пр(8.12)

Графики процессов изменения электромагнитного момента и скорости при отработке скачкообразных возмущений по управлению и моменту нагрузки представлены на рис.8.3 а и б. Кривые отличаются от соответствующих кривых для случая вещественных корней только характером свободных составляющих. Все выводы относительно времени и качества процессов были сделаны при анализе переходных характеристик в соответствующем разделе.

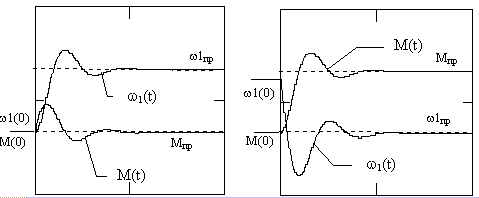
Рис. 8.3, а, б.