Лекция 7

ДИНАМИЧЕСКИЕ СВОЙСТВА ОБОБЩЕННОГО ЭМП С ЛИНЕЙНОЙ МЕХАНИЧЕСКОЙ ХАРАКТЕРИСТИКОЙ

Система уравнений, описывающих указанный ЭМП, известна (лекция 5) :

Tэ dM/dt = b (w 0-w 1) - M,

JS dw 1/dt= M- Mc.

Вводя понятие электромеханической постоянной времени обобщенного ЭМП Tм= JS /b , перепишем эту систему в виде

dM/dt = -(1/ Tэ)M - (b / Tэ)w 1+ (b / Tэ) w 0,

dw 1/dt= (1/ b Tм) M -(1/ b Tм) Mc.

Системе уравнений (7.1) соответствует приведенная на рис. 7.1 ДСС.

Рис. 7.1.

Полученную ДСС путем эквивалентных преобразований легко привести к виду

Рис. 7.2.

Принимая в качестве вектора состояния вектор

Yт =[ M w 1 ] ,

в качестве вектора управления - вектор

Uт = [w 0 Mc]

и в качестве выходных переменных сами переменные состояния , получим

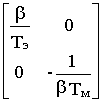A= ; B= ; Cт = .

Характеристическое уравнение ЭМП

det (l 1 - A)=0

легко приводится к виду

TэTм l 2 + Tм l +1=0

и, следовательно, собственные числа матрицы A (или корни характе-ристического уравнения) определяются выражением

.

Вводя обозначения

d = 1/2 Tэ и

получим

Как видно, в зависимости от соотношения электрической и электро-механической постоянных времени могут иметь место 3 случая :

- при d > W д корни вещественные и разные;

- при d = W д корни вещественные и равные (l 1= l 2= - d );

- при d < W д корни комплексно- сопряженные.

 

 

Передаточные функции и частотные характеристики обобщенного ЭМП

 

В системах регулирования скорости вращения интерес представляет реакция скорости w 1 на управляющее воздействие w 0 и на возмущение по нагрузке Mc, в системах регулирования момента - реакция на те же воздействия электромагнитного момента M. Эти реакции можно найти, зная соответствующие передаточные функции . Найдем передаточную матрицу исследуемого обобщенного ЭМП и определим интересующие нас передаточные функции, а также переходные и частотные характеристики соответствующих каналов.

H(p)= C(p1-A)-1 B .

(p1-A)-1 = Adj(p1-A)/det(p1-A).

Adj(p1-A)= = .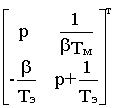

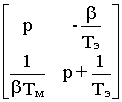det(p1-A)= (TэTм p2 + Tм p+1)/ TэTм

H(p)= [det(p1-A)]-1[1 1] ґ ґ .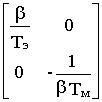

После перемножения получим

H(p)= [TэTм/( TэTм p2+ Tмp+1)] ґ .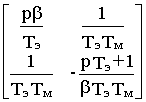

Следовательно,

Ww 1,w 0(p)=w 1(p)/w 0(p)= , (7.2)

Ww 1,Mc(p)=w 1(p)/ Mc(p)=, (7.3)

WM,w 0,=M(p)/ w 0(p)=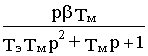 , (7.4)

WM,Mc(p)=M(p)/ Mc(p)= , (7.5)

 

Динамические характеристики канала w 0® w 1

При любых параметрах ЭМП передаточная функция указанного канала имеет вид (7.2).

При значениях Тэ таких, что 4Тэ<Тм и, следовательно d > w д , передаточная функция имеет два вещественных полюса l 1 и l 2 . При введении обозначений Т1= mod (1/l 1 ) и Т1= mod (1/l 2 ), передаточная функция (7.2) приводится к виду

Ww 1,w 0(p)=w 1(p)/w 0(p)= ,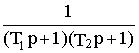

что соответствует последовательному соединению двух апериодических звеньев первого порядка с постоянными времени Т1 и Т2. Такому соединению соответствует переходная характеристика h(t) вида

h(t)= L-1{W(p)/p}= 1+ -.

ЛАХ и переходная характеристика канала для данного случая пред-ставлены на рис. 7.3, а и б.

  

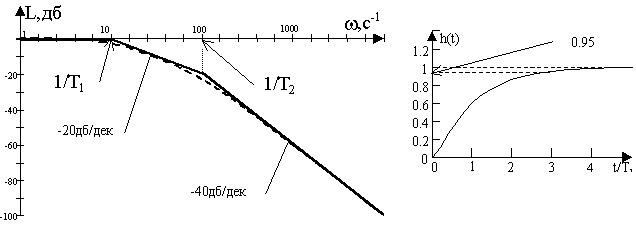
Рис. 7.3, а Рис. 7.3, б

Как видно, реакция скорости на скачок управления носит апериодический характер и время ее определяется приближенно как 3T1. Это время растет с ростом электрической и механической постоянной времени при сохранении соотношения постоянных 4Тэ<Тм.

При 4Тэ=Тм характеристическое уравнение системы имеет два равных вещественных корня l 1= l 2= - d = -1/2Тэ. Передаточная функция (7.2) принимает при этом вид

Ww 1,w 0(p)=w 1(p)/w 0(p)= ,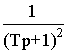

где Т=2Тэ, что соответствует последовательно включенным одинаковым апериодическим звеньям первого порядка. Переходная характеристика ЭМП описывается выражением

h(t) = 1- (1+d t)e-d t =1- (1+t/2Tэ) e-t/2Tэ.

Как видно и в этом случае переходная характеристика носит апе-риодический характер, при этом время процесса составляет величину tп= 6Тэ. ЛАХ и переходная характеристика канала для данного случая представлены на рис. 7.4, а и б.

 

Рис. 7.4, а Рис. 7.4, б 

При 4Тэ>Тм корни характеристического уравнения ЭМП становятся комплексно-сопряженными и принимают вид

l 1,2=-d ± jW св,

где W св=Ц W д2 - d2 - частота свободных колебаний .

Общее выражение передаточной функции ЭМП приобретает вид передаточной функции колебательного звена

Ww 1,w 0(p)=w 1(p)/w 0(p)= ,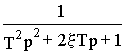

где постоянная времени T и коэффициент затухания x определяются выражениями

T=Ц Tэ Tм и x = Tм/ 2Ц Tэ Tм = d /W д

Частотные характеристики колебательного звена, соответствующие значениям x =1, x =0.71 и x =0.35 приведены на рис. 7.5,а.

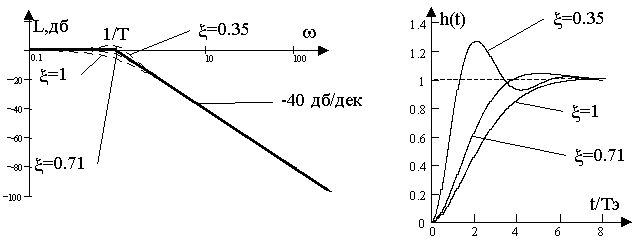
Рис. 7.5, а Рис. 7.5, б 

Они показывают, что при уменьшении x колебательность ЭПМ возрастает и при x < 0.71 в ЛАЧХ проявляется резонансный пик, быстро возрастающий с уменьшением x .

Переходная функция канала w0®w1 определяется в рассматриваемом случае выражением

h(t)= 1 -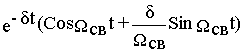

На рис. 7.5,б представлен ряд зависимостей h(t), соответствующих различным значениям x .

Анализ этих кривых, а также выражения для h(t) , что

а) время затухания колебаний зависит только от электрической постоянной времени Тэ и определяется как tп= 6 Тэ;

б) с ростом постоянной времени Тэ при неизменной электромеханической постоянной времени Тм растет время переходного процесса и при этом возрастает частота свободных колебаний W св;

в) При x = 0.71 колебания затухают практически за один период, а скорость w1 достигает установившегося значения с превышением его в переходном процессе (перерегулированием) около 5%. При x <0.71 затухание колебаний ухудшается и перегулирование сильно возрастает.

Мы здесь не будем проводить столь же детальный анализ динамических характеристик всех каналов. Имея описание в пространстве состояний, это легко сделать по аналогичному алгоритму. Здесь отметим все же следующее:

1. Переходные процессы по характеру и длительности для всех каналов одинаковы, поскольку определяются одними и теми же корнями (собственными числами).

2. Для каналов Mc® w 1 и w0® M при одинаковых прочих параметрах следует ожидать больших по величине динамических отклонений (перемахов и перерегулирований) из-за наличия в их составе дифференцирующих звеньев (форсирующего звена первого порядка и идеального дифференцирующего звена).

3. С позиций обеспечения условий устойчивости замкнутой системы каналы Mc® w1 и w0® M благоприятнее остальных по той же причине, поскольку диапазон изменения фазового сдвига в диапазоне частот входного воздействия w М (0, Ґ ) ограничен величиной 0 - -90 град.

4. Передаточная функция канала Mc® w1 имеет знак (-), указывающий на то, что с увеличением момента сопротивления (нагрузки) скорость двигателя падает из-за падающей механической характеристики ЭМП.

5. Канал w0®M не имеет статической характеристики. Это значит, что электромагнитный момент после окончания переходного процесса возвращается к одному и тому же установившемуся значению, не зависящему от управляющего воздействия w0 . Оно определяется приложенным моментом нагрузки Mc.