
Лекция 5
Математические модели обобщенной ЭПС
.Как известно, ЭПС современной ЭМС функционально содержит три основных узла: механизм Мх, включающий передаточный механизм и рабочий орган. электромеханический преобразователь энергии ЭМП (электрическая машина) и управляемый преобразователь электрической энергии УП. Для анализа наиболее общих закономерностей, характерных для ЭМС при регулировании момента, скорости
и положения независимо от технической реализации реальная ЭПС, как объект управления, часто заменяется математической моделью, называемой обобщенной энергетической подсистемой. Математическая модель содержит те же функциональные узлы , что и реальная ЭПС. Специфика конкретных систем отражается в значении обобщенных параметров.Расчетные схемы и уравнения механической части.
В общем случае механическая часть представляет собой систему связанных масс, движущихся с различными скоростями вращательно или поступательно. При нагружении элементы системы (валы , опоры, клиноременные передачи, зубчатые зацепления и т.п., деформируются, так как механические связи не являются абсолютно жесткими. Входной вал механизма приводится во вращение со скоростью
w 1 электромагнитным моментом M, возникающим на роторе ЭМП (двигателя).Исследования динамики показывают, что в большинстве практических случаев реальные механизмы могут быть сведены к трехмассовой, двухмассовой и одномассовой расчетным схемам.
Параметрами обобщенной трехмассовой механической системы (рис. 5.1) являются суммарные приведенные моменты инерции масс J
1, J2 и J3 и эквивалентные приведенные жесткости механических упругих связей C12 и C23.
Рис. 5.1.
Здесь
Cik = d Mi / d j k - жесткость связи. При абсолютно жесткой связи соответствующий коэффициент равен Ґ .Первая масса представляет собой ротор двигателя и жестко с ним связанные элементы. К этой массе приложен электромагнитный момент двигателя M и момент статической нагрузки M
c1. который обычно является суммарным моментом потерь на валу двигателя и жестко связанных с ним элементах. К промежуточной массе механизма приложен момент сопротивления Mc2 и к третьей - момент внешней нагрузки Mc3.Трехмассовая модель при исследовании ЭМС используется в тех случаях, возникает необходимость более детального анализа условия движения масс механизма. Для решения задачи при этом обычно используется математическое моделирование на ЭВМ, поскольку аналитическое решение получается весьма громоздким.
Двухмассовая модель, упрощенно представленная на рис.5.2, наиболее удобна для изучения влияния упругости механических связей на поведение ЭМС и в данном курсе для нас будет являться основной.
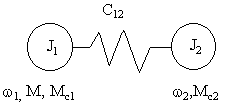
Рис. 5.2.
Поведение двухмассовой системы можно описать следующей системой уравнений, составленных на основании второго закона Ньютона

Дифференцируя обе части уравнения 5.1, б, получим
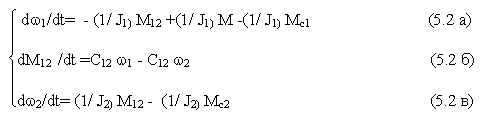
В тех случаях, когда параметры системы таковы, что влияние упругих связей незначительно, или при решении задач, в которых с этим влиянием можно не считаться, механическая часть представляется простейшей расчетной схемой, не учитывающей влияние упругих связей-жестким приведенным звеном. В этом случае многомассовая система заменяется одной эквивалентной массой с моментом инерции J
S , на которую воздействует электромагнитный момент двигателя M и суммарный приведенный к валу двигателя момент нагрузки Mc. Последний включает в себя все внешние силы, приложенные к механической системе, кроме момента двигателя M.Приведем двухмассовую систему (рис.5.2) к одномассовой, предположив связь между первой и второй массами абсолютно жесткой. Отличием ее от ранее рассмотренной системы является равенство скоростей масс
w 1 = w 2 = w . а также M12=0. Складывая уравнения 5.1 а и 5.1б , получимJ
S dw /dt= M- Mc,где J
S = J1+J2 и Mc= Mc1 + Mc2Уравнение 5.3 представляет собой основное уравнение движения электропривода. Его значение для анализа физических процессов в ЭМС исключительно велико. Оно правильно описывает движение механической части любой ЭМС в среднем. Поэтому с его помощью можно по известному электромагнитному моменту двигателя и значениям J
S и Mc оценить среднее значение ускорения электропривода, предсказать время, за которое двигатель достигнет заданной скорости и решить многие другие практические вопросы даже в тех случаях, когда влияние упругих связей в системе существенно.Обобщенная модель ЭМП с линеаризованной механической характеристикой
Анализ электромеханических свойств двигателей различного вида показывает, что при определенных условиях механические характеристики принципиально разнотипных двигателей описываются идентичными уравнениями. Соответственно в этих границах аналогичны и основные электромеханические свойства двигателей, что создает предпосылки для обобщенного изучения динамики электромеханических систем.
Для описания электромеханических процессов в любом ЭМП как электромеханической системе можно использовать системы уравнений 5.1, 5.2 или 5.3 в сочетании с уравнением динамической жесткости. Для ЭМП с линеаризованной механической характеристикой последнее может быть записано в виде
T
э dM/dt = b (w 0-w 1) - M,где
b = M/(w 0-w 1) - статическая жесткость, Tэ-электромагнитная постоянная времени и w 0 - обобщенное входное воздействие в виде скорости холостого хода обобщенного ЭМП. Из выражения 6.4 можно найти операторное изображение динамической жесткости в виде![]()
и установить, что она описывается передаточной функцией апериодического звена первого порядка.
Естественно, что выражение 5.4 для различных типов двигателей отличаются значениями статической жесткости, электромагнитной постоянной времени и обобщенного входного воздействия. Особенности применяемого двигателя при этом отражаются в конкретном смысле переменных и выражениях параметров.
Например, для двигателя с независимым возбуждением (с постоянным магнитным потоком Ф и якорным управлением коэффициенты обобщенного уравнения определяются следующим образом
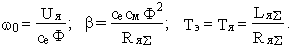
Для асинхронного двигателя при линеаризации рабочего участка его характеристики в области s
< s кр эти параметры определяются соотношениями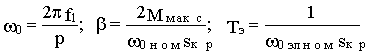
Аналогичные соотношения могут быть найдены и для ДПТ с полюсным управлением и для синхронного двигателя. Однако они будут рассмотрены в соответствующих курсах.
Обобщенная электромеханическая система с механической характеристикой, описываемой линейным дифференциальным уравнением первого порядка является основным объектом изучения теории ЭМС. Она правильно отражает основные закономерности, свойственные реальным нелинейным ЭМС в режимах допустимого отклонения от статического состояния и благодаря простоте обеспечивает возможность обобщенного анализа этих закономерностей методами теории автоматического управления.
Обобщенный управляемый электрический преобразователь
Управляемый преобразователь электрической энергии при построении математических моделей первого приближении можно описать дифференциальным уравнением первого порядка следующим образом
T
пр dw 0/dt= Kпр uу - w 0где uу - входное управляющее воздействие (выходной сигнал регулятора в замкнутой системе;
w 0- выходной сигнал преобразователя; Tпр и Kпр - соответственно постоянная времени и статический коэффициент передачи преобразователя. Как видно описание преобразователя соответствует апериодическому звену первого порядка с передаточной функцией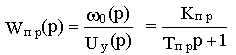
Уравнения состояния и структурная схема обобщенной электромеханической системы.
Объединяя уравнения 5.6, 5.4 и 5.2 в систему и разрешая их относительно соответствующих производных, получим систему уравнений состояния обобщенной ЭПС с двухмассовой механической подсистемой в виде 5.7
d
w 0 /dt= -(1/ Tпр ) w 0 +(Kпр / Tпр ) uуdM/dt = (
b / Tэ) w 0- (b / Tэ)w 1 -(1/ Tэ)M,d
w 1/dt= - (1/ J1) M12 +(1/ J1) M -(1/ J1) Mc1dM12 /dt =C12
w 1 - C12 w 2d
w 2/dt= (1/ J2) M12 - (1/ J2) Mc2Принимая в качестве вектора состояния вектор
Y
т =[ w 0 M w 1 M12 w 2 ] ,в качестве вектора управления - трехмерный вектор
U
т = [ uу Mc1 Mc2 ]и в качестве выходных переменных сами переменные состояния , получим
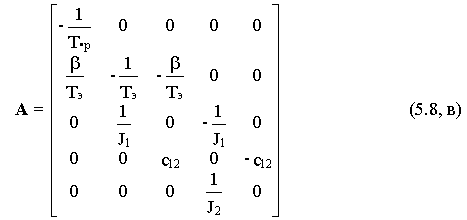

Этой системе уравнений соответствует приведенная ниже ДСС, которая может быть использована в качестве имитационной модели обобщенной энергетической подсистемы ЭМС
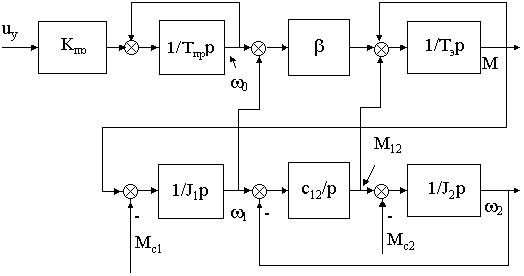
Рис. 5.3.
Как видно, обобщенная ЭПС даже при представлении механизма двухмассовой моделью описывается системой дифференциальных уравнений 5-го порядка и доступна точному анализу лишь на ПЭВМ (на цифровой модели). Учитывая трудоемкость теоретического анализа полной системы и громоздкость аналитических выражений, описывающих электромеханические процессы в обобщенной ЭПС, специфику этих процессов мы выясним, проведя далее анализ этих процессов отдельно для механической подсистемы и отдельно для электромеханической подсистемы с одномассовой моделью механизма