Лекция 4
СОСТАВЛЕНИЕ ДСС ПО ПЕРЕДАТОЧНОЙ ФУНКЦИИ
Схема системы в переменных состояния может быть составлена по передаточной функции тремя способами: методом прямого программирования, методом параллельного программирования и методом последовательно программирования.
Метод прямого программирования
Этот метод позволяет представить систему уравнений состояния в нормальной канонической форме по известной передаточной функции звена или системы с одним входом и одним выходом.
Известно, что системе с передаточной функцией
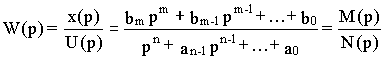
соответствует дифференциальное уравнение
![]()
или
N(p) x= M(p) u,
где P
i = di / dtiРассмотрим вначале систему с передаточной функцией
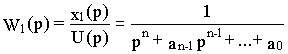 ,
,![]() (4.1)
(4.1)
которой соответствует дифференциальное уравнение

![]() (4.2)
(4.2)
Введем обозначения: y
1= x1 и![]()
Следовательно, система уравнений состояния, соответствующая передаточной функции (4.1) , м.б. записана в виде
![]()
![]()
. . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
![]()
Записывая эту систему в векторно -матричной форме, получим
A
=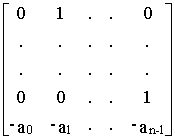 B=
B=Используя уже известные правила, построим Д
CС по уравнениям состояния в виде рис. 4.1. :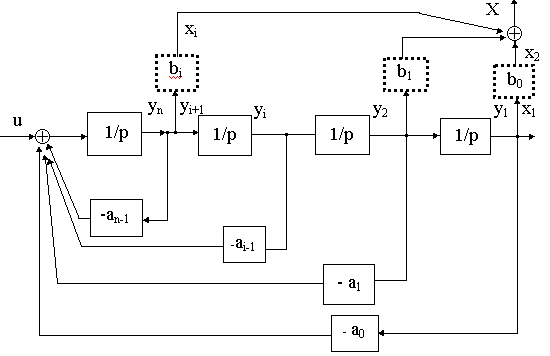
Рис. 4.1.
Рассмотрим теперь систему с передаточной функцией
 ,
, ![]() (4.3)
(4.3)
которой соответствует дифференциальное уравнение
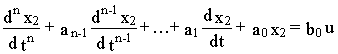
![]() (4.4)
(4.4)
Подстановкой x
1=x2/ b0 уравнение (4.4) сводится к (4.2) и следовательно ,- уравнения состояния, соответствующие передаточным функциям (4.1) и (4.3) разнятся только масштабом выходной переменной и, следовательно, только элементами матрицы С
. Для последнего случаяC
=- в ДСС появляется дополнительное масштабирующее звено с коэффициентом передачи b
0 , со входом y1 и выходом x2 . Это звено выделено жирной штриховой линией на рис. 4.1.Рассмотрим далее систему с передаточной функцией
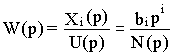 (4.5)
(4.5)
Этой передаточной функции соответствует дифференциальное уравнение
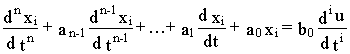
![]() (4.6)
(4.6)
Выходную величину X
i можно представить в операторной форме выражением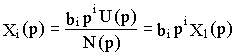
Переходя к функции времени, получим
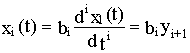
Следовательно, ДСС данной системы с передаточной функцией (4.5) может быть получена из ДСС уже известной системы путем введения масштабирующего звена с коэффициентом передачи b
i, входом yi+1 и выходом xi. В уравнениях состояния изменятся лишь элементы матрицы С. Последняя будет иметь видC
=Таким образом выходную величину исходной системы с передаточной функцией
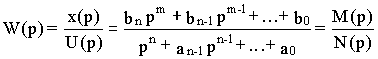
можно представить в виде суммы в соответствии с числом слагаемых полинома числителя M(p), т.е.
![]()
Переходя к функции времени, получим

или с учетом ранее введенных обозначений
![]()
Следовательно, структурная схема исходной системы отличается от ранее полученных наличием полного набора масштабирующих звеньев ( всего их m+1 ) c коэффициентами передачи b
i в цепи формирования выходной переменной x. (см. рис. 4.1.)Матрицы А и В всех рассмотренных систем одинаковы. Их элементы формируются из коэффициентов полинома знаменателя передаточной функции.
Коэффициенты полинома числителя определяют только элементы матрицы С и влияют лишь на формирование выходной переменной. В последнем наиболее общем случае матрица С имеет вид
C
=Пример1: Составить ДСС и систему уравнений состояния для звена с передаточной функцией
![]()
Приведем передаточную функцию звена к стандартному виду
![]()
![]() ,
,
где a
0=1/T2, b0=1/T2, b1=T1/T2Стандартной передаточной функции соответствует стандартная ДСС:
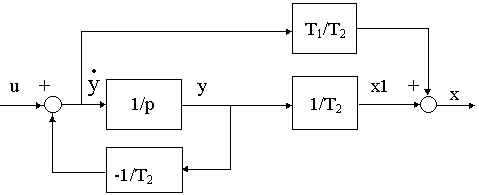
Рис. 4.2.
и система уравнений состояния первого порядка
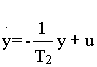

Рассмотрим еще пример:
Составить ДСС и уравнения состояния для системы, заданной передаточной функцией

Приводя запись передаточной функции в стандартную форму, получим: a
2=7, a1=12, a0=0, b2=1, b1=3, b0=2.ДСС изобразим в стандартном виде
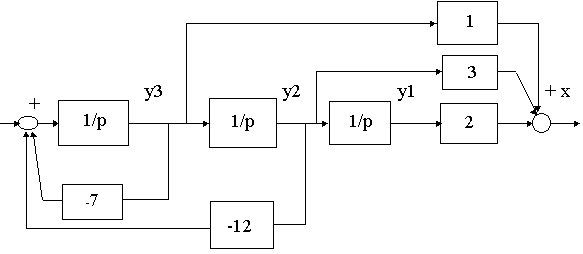
Рис. 4.3.
Система уравнений состояния для этого случая в обычной форме
![]()
![]()
![]()
![]()
В матричной форме
A
=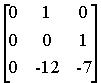 B=
B=
ПАРАЛЛЕЛЬНОЕ ПРОГРАММИРОВАНИЕ
При указанном подходе передаточная функция исходной системы представляется в виде суммы передаточных функций однотипных звеньев следующим образом:
![]()
Здесь
l i -корни полинома знаменателя передаточной функции, а a i - находятся по формуле![]() при p=l i
при p=l i
Такая передаточная функция соответствует параллельному соединению n однотипных звеньев со структурными схемами, представленными на рис. 4.4 .

Рис. 4.4.
Выходные сигналы x
i звеньев суммируются .Используя эту методику, составим ДСС для рассмотренной выше системы. Корни знаменателя равны :
l 1 =0, l 2=-3, l 3 =-4.Вычисляя коэффициенты числителей, получим
a 1=1/6, a 2=-2/3, a 3=3/2. Тогда структурная схема системы примет вид (рис.4.5.)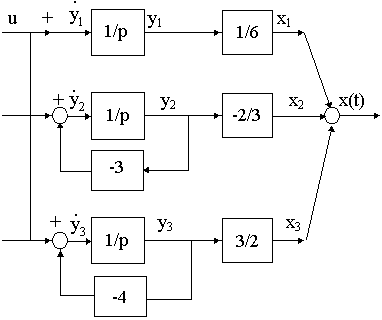
Рис. 4.5.
Этой структурной схеме соответствует следующая система уравнений состояния
A= 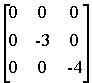 B=
B= ![]() CT=
CT= D=0
D=0
ПОСЛЕДОВАТЕЛЬНОЕ ПРОГРАММИРОВАНИЕ
Для составления ДСС этим методом исходная передаточная функция представляется в виде произведения дробно-рациональных функций, порядок полиномов знаменателя и числителя которых не превышает единицы. Если порядки числителя и знаменателя исходной передаточной функции одинаковы, т.е. m=n, то последняя записывается в виде
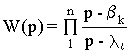
где
bk и lk - соответственно корни полинома числителя (нули) и корни полинома знаменателя (полюса). Если n>m (что практически всегда имеет место), то (n-m) сомножителей имеют в числителе единицу. Стандартная ДСС для элементарной дробно-рациональной функции общего вида нами была ранее, по существу, обоснована. Она изображается в виде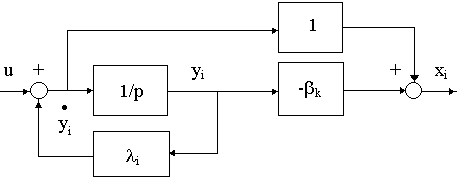
Рис. 4.6.
Поскольку произведение передаточных функций соответствует последовательному соединению звеньев, ДСС исходной системы будет содержать n последовательно соединенных ДСС идентичной конфигурации.
Передаточную функцию уже рассмотренной системы представим в виде произведения трех дробей
![]()
ДСС соответствует последовательному соединению ДСС элементарных звеньев и имеет следующий вид
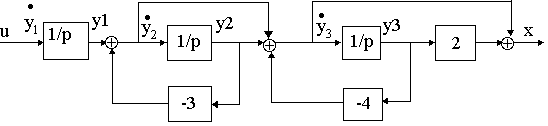
Рис. 4.7.
Этой ДСС соответствует следующая система уравнений состояния
![]()
![]()
![]()
![]() ,
,
в матричной форме принимающая следующий вид
A
=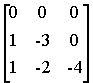 B=
B= Следует подчеркнуть, что для одной и той же системы можно составить несколько схем в переменных состояния, отличающихся природой промежуточных переменных, выбранных для описания системы. Различному выбору переменных состояния соответствуют различные матрицы системы, управления и наблюдения и различные векторные дифференциальные уравнения.