Лекция 3
СТРУКТУРНЫЕ СХЕМЫ СИСТЕМ В ПЕРЕМЕННЫХ СОСТОЯНИЯ
Из материала лекции 2 видно, что определение передаточной функции системы по уравнениям состояния требует обращения матрицы (p
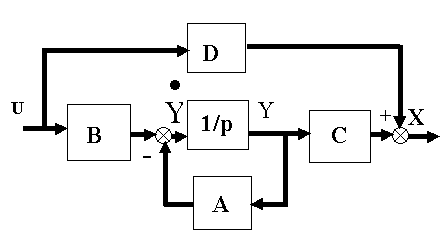
1-A), что в случае высокой размерности последней может представить значительные трудности. Использование структурной схемы системы в переменных состояния существенно облегчает поставленную задачу.На рис. 3.1 показана обобщенная структурная схема системы, соответствующая векторно-матричным дифференциальным уравнениям (2.5) и (2.6).
Жирные линии на рисунке характеризуют векторные связи. Символ 1/p означает операцию интегрирования.

Рис.3.1.
Матричную структурную схему используют при описании сложных многосвязных систем.
На практике более удобными являются детализированные структурные схемы или схемы в переменных состояния. Они состоят только из элементарных звеньев: интегрирующих, усилительных и суммирующих. Говоря строго, детализированная структурная схема (ДСС) - это математическая модель, состоящая только из элементарных звеньев -интегрирующих, масштабирующих и суммирующих, в том числе нелинейных, с полностью вскрытыми связями между ними. Выходные переменные интеграторов принимаются в качестве переменных состояния.
ДСС для системы первого порядка легко получается из обобщенной векторно-матричной структурной схемы. Так в случае, если A=a, B=b, C=c, D=d, имеем
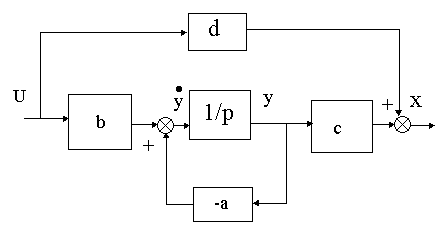
Рис.3.2.
В частности b=a=1/T, c=1, d=0 имеем детализированную структурную схему
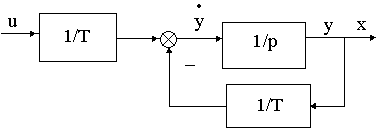
Рис.3.3
апериодического звена первого порядка с передаточной функцией
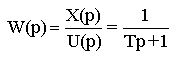
Схему в переменных состояния можно составить либо непосредственно по уравнениям состояния, либо по передаточным функциям.
СОСТАВЛЕНИЕ ДСС ПО УРАВНЕНИЯМ СОСТОЯНИЯ
Для составления ДСС по уравнениям состояния целесообразно
1. Изобразить n интегрирующих звеньев с передаточными функциями 1/p, где n - порядок системы. Обратим внимание на то обстоятельство, что выходной величиной интегратора является переменная состояния y
i, а входной - ее производная d yi /dt, т.е.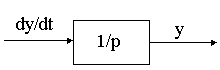
2. Используя операции суммирования и масштабирования, организовать связи между входами и выходами интеграторов в соответствии с уравнениями (2.5).
3. Используя операции суммирования и масштабирования , огранизвать связи между переменными состояния в соответствии с уравнениями (2.6).
В качестве примера составим ДСС уже известного нам ДПТ по его уравнениям (2.9)
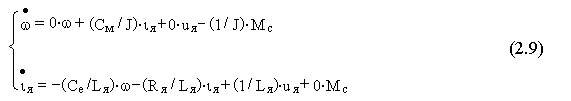
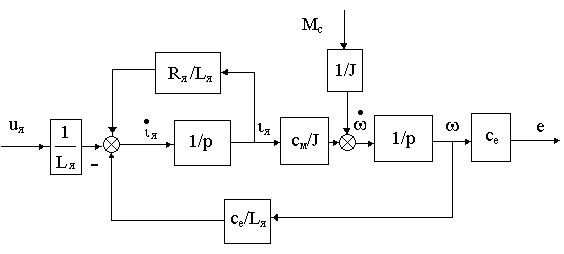
Рис. 3.4.

Рис. 3.5.
Составив схему в переменных состояния и применив правила преобразований, легко составить по ней передаточные функции по всем координатам и управляющим воздействиям. Определим, например, уже известные нам передаточные функции ДПТ на основании преобразованной структурной схемы, приведенной на рис. 3.6.
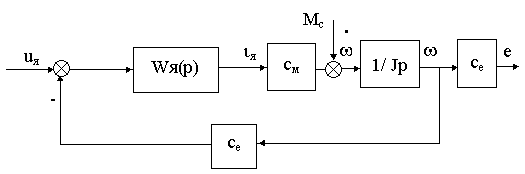
Рис. 3.6.

Итак в ряде случаев короче оказывается путь нахождения передаточной функции по уравнениям состояния через ДСС и ее эквивалентные преобразования.