Лекция 24
Трехконтурная система регулирования скорости
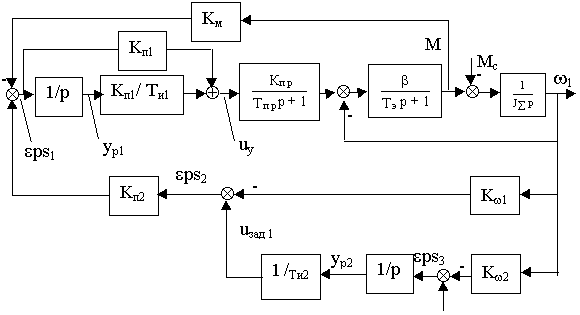
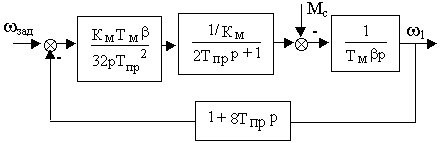
Структурная схема системы изображена на рис.24.1. Система содержит внутренний подчиненный контур регулирования момента с известной структурой и два внешних контура регулирования скорости. Первый внешний контур содержит П-регулятор с коэффициентом передачи Kп2 и датчик скорости с коэффициентом передачи K
w1. Второй внешний контур содержит И-регулятор с постоянной времени Ти2 и датчик скорости с коэффициентом передачи Kw2.
Рис.24.1
Математическая модель системы содержит 5 уравнений состояния
T
пр dw0/dt= - w0 +Kпр uуT
эJS ![]() = M- Mc
= M- Mc
![]() = e1
= e1
![]() = e3
= e3
где к известным переменным состояния, характеризующим энергети-ческую подсистему ЭМС, добавлен выхол интегратора ПИ-регулятора момента y
p1, и выход интегратора И-регулятора внешнего контура регулирования скорости yp2.Для формирования модели к уравнениям состояния следует добавить уравнения связей, по существу формирующие из задающего воздействия и координат состояния управляющее воздействие Uу на входе управляемого преобразователя (или на входе энергетической подсистемы). Как видно последнее связано с ошибками
eps3 (на входе регулятора внешнего контура регулирования скорости, eps2 (на входе регулятора внутреннего контура регулирования скорости) и eps1 (на входе регулятора момента)e
ps3= uзад - Кw2 w1e
ps2= yp2/ Ти2 - Кw1w1e
ps1= eps2Кп2 - Км Мu
у=eps1Кп1 +(Кп1/Ти1)yp1Оптимизация контуров регулирования
Внутренний (подчиненный) контур регулирования момента имеет унифицированную структуру, настраивается с использованием ПИ-регулятора на технический оптимум и имеет передаточную функцию
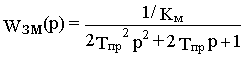 ,
,
или после известного упрощения
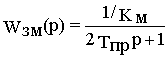 .
.
Передаточная функция первого внешнего контура регулирования скорости с П-регулятором при настройке на технический оптимум по управлению имеет вид
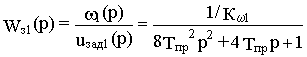
или после упрощения
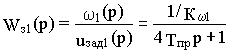 .
.
Условие оптимизации
Кп2=КмТм
b /4 Тпр Kw1было получено в лекции 22.
Тогда передаточную функцию разомкнутого второго внешнего контура регулирования скорости можно записать так
 ,
,
где
eps*3= eps3/ Kw2.Принимая в качестве малой некомпенсируемой постоянной времени величину Т
m3=4 Тпр, получим условие настройки контура на технический оптимум в виде2Т
m3=8 Тпр = Ти2 Kw1 /Kw2или Ти2 = 8 Тпр
Kw2 /Kw1
При этом передаточная функция замкнутой системы вцелом по задающему воздействию примет вид
 ,
,
где
w зад= uзад/ Kw2.Этой системе соответствует переходная характеристика с временем процесса tп= 24 Тпр, не отличающемся от времени его в двукратно-интегрирующей системе, но с перерегулированием, не превышающим 4,3%, как в обычном контуре с настройкой на технический оптимум. По отношению к контуру с настройкой на симметричный оптимум оно меньше в 10 раз и для уменьшения его не требуется установка входного сглаживающего фильтра.
Оценим далее свойства рассматриваемой трехконтурной системы по отношению к возмущениям в виде изменения статического момента нагрузки. Для этого проведем следующие структурные преобразования

Далее с учетом условий оптимизации (24.1) и (24.2)

Далее
Окончательно
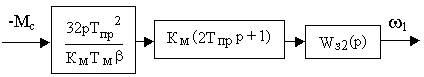
и
W
в(p)= w 1(p)/Mc(p)= .
.
Полученная передаточная функция идентична соответствующей передаточной функции по возмущению двукратноинтегрирующей системе регулирования скорости, настроенной на симметричный оптимум, если в знаменателе последней пренебречь слагаемым с р
3. Следовательно, для данной системы справедливы относительно возмущения все те выводы, которые были сделаны для ранее рассмотренной системы.