УНИФИЦИРОВАННЫЕ СИСТЕМЫ РЕГУЛИРОВАНИЯ СКОРОСТИ

Лекция 22

СИСТЕМЫ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ СКОРОСТИ

Общие принципы построения систем подчиненного регулирования, их преимущества и недостатки были рассмотрены в лекции 15. Системы подчиненного регулирования скорости содержат внутренний (подчиненный) контур регулирования момента и один или два внешних контура регулирования скорости.

Двухконтурная система с П-регулятором скорости

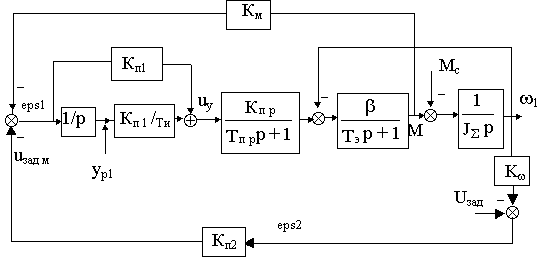
Структурная схема системы с П-регулятором скорости представлена на рис. 22.1. Структурная схема контура регулирования момента не отличается от рассмотренной в лекции 17 (см. рис. 17.1). ПИ- регулятор момента с коэффициентом передачи К_п1 и временем изодрома Т_и представлен на рис.22.1 детализированной структурной схемой. Через eps₁и eps₂обозначены ошибки соответственно на входах контуров регулирования момента и скорости. П-регулятор скорости имеет коэффициент передачи К_п2, а его выходное напряжение u_{зад м}является задающим для подчиненного контура регулирования момента.

Рис.22.1

Математическая модель системы содержит 4 уравнения

T_пр dw₀/dt= - w₀+K_пр u_у

T_э = b w ₀ - M- b w₁,

JS = M- M_c

= eps₁

где к известным переменным состояния, характеризующим энергетическую подсистему ЭМС, добавлена выходная координата интегратора ПИ-регулятора скорости y_p1.

Для формирования модели к уравнениям состояния следует добавить уравнения связей, по существу формирующие из задающего воздействия и координат состояния управляющее воздействие U_уна входе управляемого преобразователя (или на входе энергетической подсистемы). Как видно последнее связано с ошибками e₂(на входе регулятора скорости) и e₁(на входе регулятора тока)

e₂₌u_зад - К_ww₁

e₁₌e₂К_п2 - К_мМ

u_у=e₁К_{п1 +}(К_п1/Т_и1)y_p1

Исключая переменные (в виде ошибок) из уравнений связи (последовательно, начиная с первого), получим

u_у= К_п1 К_п2 u_зад - К_п1 К_п2 К_ww₁- К_п1 К_мМ +(К_п1/Т_и1)y_p1

Оптимизация контуров регулирования

Внутренний (подчиненный ) контур регулирования момента имеет унифицированную структуру (рис.22.2).

Рис.22.2

Контур настраивается на технический оптимум. Покольку обычно Т_э>>Т_пр и, кроме того, инерционность преобразователя по условию компенсировать нельзя и не имеет смысла, то примем постоянную времени преобразователя в качестве малой некомпенсированной постоянной (Т_пр=Т_m1) и выберем время изодрома регулятора из условия компенсации постоянной времени Т_э. Тогда передаточная функция разомкнутого внутреннего контура примет вид

Оптимизируя контур, найдем

2T_пр = Т_э/ К_пр К_п1К_мb_®К_{п 1}=Т_э/ 2К_прbT_пр К_м

Передаточная функция замкнутого контура регулирования момента примет вид

или после известного упрощения

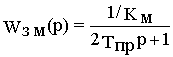Тогда расчетная структурная схема контура регулирования скорости примет вид

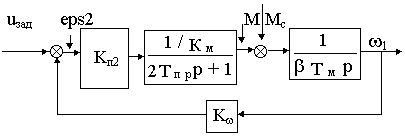
Рис. 22.3

или

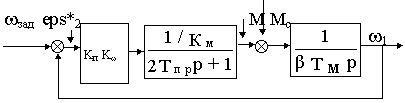
Рис. 22.4

где eps^*₂=eps₂/ K_w

Передаточная функция разомкнутого контура

W_p(p)=w₁(p)/ eps^*₂(p)= .

Настраивая контур на технический оптимум, примем в качестве малой некомпенсированной постоянной времени величину 2Т_пр =Т_m2=2Т_m1. Коэффициент передачи П-регулятора скорости получим из условия

2Т_m2= К_мТ_мb/ К_п2К_w

Следовательно, К_п2 = К_мТ_мb/ К_w 4Т_пр

Статические и динамические характеристики контура с такими настройками относительно задающего (управляющего) воздействия соответствуют характеристикам стандартной системы, настроенной на технический оптимум. Передаточная функция замкнутого контура по заданию имеет вид

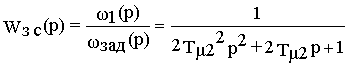или

При этом

а) контур не имеет статической ошибки, пропорциональной сигналу задания (система обладает астатизмом первого порядка по управлению)

б) время переходного процесса по управлению составляет величину

t_п @ 6 Т_m2 @ 12 Т_m1 @ 12 Т_пр ,

однозначно определяется величиной постоянной времени управляемого электрического преобразователя и вдвое превышает время переходного процесса в контуре регулирования момента. Последнее является характерным свойством систем подчиненного регулирования: при настройке контуров на технический оптимум: быстродействие внешнего контура вдвое меньше быстродействия подчиненного внутреннего контура.

Рассмотрим далее характеристики контура относительно возму-щающего воздействия (момента нагрузки М_с)

Преобразуя схему известным образом, получим

Рис.22.5

Передаточная функция системы по возмущению после замены замкнутого контура регулирования скорости эквивалентным апериодическим звеном равна

или с учетом выражения для коэффициента передачи П-регулятора оптимизированного контура

К_п2 = К_мТ_мb/ К_w4Т_пр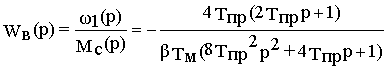

Найдем операторное изображение скорости w₁(p), при нулевых начальных условиях и нулевом задающем воздействии представляющем собой ошибку контура Dw(p), обусловленную постоянным моментом статической нагрузки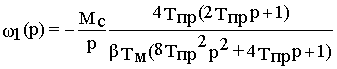

Находя установившееся значение ошибки в системе как,

установим, что

1. Эта ошибка отлична от нуля при любом ненулевом моменте нагрузки М_с , и следовательно, в пределах зоны пропорциональности УПП механические характеристики определяются выражением

w₁=w_зад + Dw_уст

и по форме не отличаются от аналогичных характеристик одноконтурной системы регулирования скорости с П-регулятором.

2. Жесткость механических характеристик замкнутого контура определяется выражением

b_{ск =}b(Т_м/4 Т_пр)

и при определенном соотношениии параметров (Т_м/4Т_пр)<1 (т.е. при малых Т_м) может быть ниже, чем жесткость характеристик собственно ЭМП (b).

Используя операторное изображение ошибки контура, возникающей при парировании возмущения по моменту и известную формулу разложения, нетрудно установить, что временная зависимость Dw₁(t) имеет вид

Dw₁(t) =Dw_уст ().

График, соответствующий этой зависимости представлен на рис.22.6.

Рис.22.6

Как видно,

а) процесс парирования - колебательный с перерегулированием, не превышающем значения 5 %;

б) время парирования соответствует стандартному и составляет величину t_п @ 12 Т_пр.

Стандартная настройка контура регулирования скорости на технический оптимум широко используется на практике в связи с простотой технической реализации и благоприятным в большинстве случаев характером протекания переходных процессов. Однако, как было установлено, точность регулирования при малом моменте инерции нагрузки может быть ниже, чем в разомкнутой системе и не удовлетворять техническим требованиям. В этих случаях в унифицированных структурах прибегают к увеличению порядка астатизма по отношению к воздействию нагрузки.