2. Одконтурная система с ПИ-регулятором скорости

Лекция 21

Одноконтурная система с ПИД-регулятором скорости

Анализируя характеристики одноконтурной системы с ПИ-регулятором, можно сделать вывод о том, что уменьшение времени реакции на скачок задающего воздействия и динамических ошибок при парировании скачкообразных возмущений по нагрузке связано с уменьшением некомпенсированной постоянной времени Т_m. В рассмотренном выше случае Т_m = Т_пр + Т₂, или при Т_m>10Т_э ® Т_m @ Т_пр + Т_э. Следовательно, постоянную времени Т_m можно уменьшить, компенсируя электромагнитную постоянную времени ЭМП Т_э. Компенсацию можно осуществить с использованием ПИД-регулятора в контуре управления. При этом нет ограничения на соотношение постоянных времени Т_м и Т_э.

Структурная схема и математическая модель системы

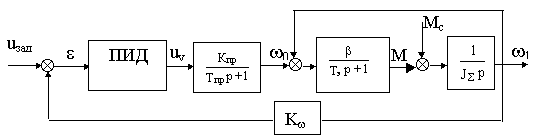
Исходная структурная схема системы представлена на рис.21.1

Рис.21.1

Дополним систему уравнений состояния разомкнутой электромеханической системы

T_пр dw₀/dt= K_пр u_у - w₀

T_э dM/dt = b (w₀-w₁) - M,

JS dw₁/dt= M- M_c

уравнением замыкания e = u_зад - К_ww₁ и системой уравнений, описывающих ПИД-регулятор. С учетом инерционности, неизбежно появляющейся при реализации ПИД- регулятора, передаточную функцию последнего запишем в виде

W_R(p)=U_у(p)/e (p)= ,

где Т_v- постоянная времени дополнительного инерционного звена или

W_R(p)=U_у(p)/e (p)=

Используя известный нам метод прямого программирования составим структурную схему системы в переменных состояния

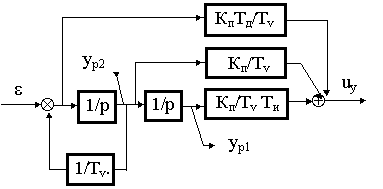
Рис.21.2

где y_p2 и y_p1-выходные координаты (переменные состояния) интеграторов модели ПИД-регулятора.

Уравнения состояния ПИД-регулятора примут при этом вид

= e - (1/T_v)

u_у= (К_п/Т_v Т_и.)y_p1+ (К_п/Т_v )+ (К_пТ_д/Т_v).

После подстановки e из уравнения замыкания системы, получим

= u_зад - Кw _{w 1}- (1/T_v)

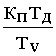u_у = y_p1+ - w 1 + u_зад

Подставляя u_у в первое уравнение исходной системы , получим математическую модель рассматриваемой одноконтурной системы с ПИД-регулятором в уравнениях состояния

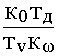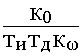T_пр = - w ₀- w ₁+ y_p1+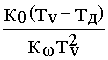+ w _зад

T_э = b w ₀ - M- b w ₁,

JS = M- M_c

= - К_ww₁- (1/T_v) + Кw _{w зад}

Видно, что для установившегося режима M= M_c и w₁ = w_зад

Следовательно, в установившемся режиме при постоянном зада-ющем и возмущающем воздействиях статическая ошибка принципиально равна нулю независимо от параметров звеньев системы и от величины внешнего возмущения М_с, т.е. w₁=w_зад.Значит механические характе-ристики указанной системы будут иметь тот же вид, что и для рассмотренной выше системы с ПИ-регулятором.

Принимая в качестве вектора состояния вектор Y^т = [w₀M w₁y_p1]

и в качестве вектора управления - вектор U^т=[ w_зад M_c ] , запишем полученную систему в стандартной матричной форме

где

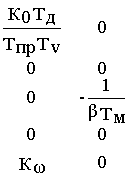
Оптимизация одноконтурной системы с ПИД-регулятором

После преобразований, как и ранее структурную схему системы изобразим в следующем виде (рис.21.3)

Рис.21.3

Заменим, как и ранее, 2 инерционных звена с малыми (относительно Т_эи Т_м) постоянными времени (преобразователь и допол-нительное инерционное звено ПИД-регулятора с постоянной времени Т_v) одним эквивалентным звеном с суммарной постоянной времени Т_m =Т_пр+ Т_v ,так что

W_р(p)=w₁(p)/ w_зад(p)=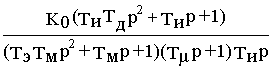

Последняя соответствует эталонной передаточной функции системы, настроенной на технический оптимум

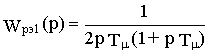
если

а) время изодрома выбрано из условия компенсации постоянной времени Т_м, т.е. Т_и=Т_м, а время предварения равно постоянной времени Т_э, т.е. Т_д=Т_э.

б) 2Т_m = Т_и/ K₀или К₀= Т_м/2Т_m. При этом коэффициент передачи ПИД-регулятора определяется выражением

К_п= Т_м/2Т_m К_пр К_w

О свойствах синтезированной таким образом системы можно сказать следующее:

1. Статические и переходные характеристики системы по управляющему воздействию соответствуют стандартному контуру, настроенному на технический оптимум, при этом быстродействие системы выше, относительно ранее рассмотренной системы с ПИ-регулятором за счет уменьшения малой некомпенсированной постоянной времени Т_m.

2. Как и ранее рассмотренная, данная система обладает астатизмом первого порядка по возмущению.