
Лекция 20
Одноконтурная схема с П-регулятором скорости
Такие системы находят применение в тех случаях, когда Тм>10Тэ , Тпр<< Тэ и по техническим требованиям допустимы статические ошибки по задающему и возмущающему воздействиям.
Исходная структурная схема системы имеет вид

Рис.20.1
и после структурных преобразований может быть изображена в виде рис.20.2

Рис.20.2
Оптимизация одноконтурной системы с П-регулятором
Передаточная функция разомкнутой системы по задающему воздействию имеет вид
W
р(p)=w 1(p)/ wзад(p)=Заменим 2 инерционных звена с малыми (относительно Т
1) постоянными времени (преобразователь и апериодическое звено с постоянной времени Т2) одним эквивалентным звеном с суммарной постоянной времени Тm =Тпр + Т2 , так чтоW
р(p)=w1(p)/ wзад(p)=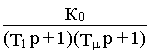
Подберем такой коэффициент передачи К
0, что частота среза ЛАХ разомкнутой системы была бы равна wc=1/2 Тm . Тогда ЛАХ можно изобразить в виде ломаной 1 на рисунке 20.3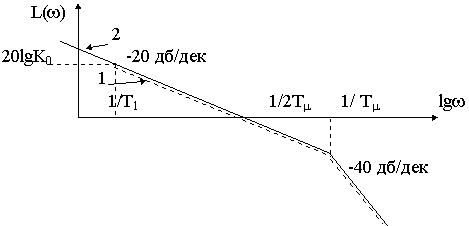
Рис.20.3
Ломаной 2 на том же рисунке изображена стандартная ЛАХ разомкнутой системы, настроенной на технический оптимум. Последняя соответствует эталонной передаточной функции

Указанные ЛАХ идентичны в среднечастотной и высокочастотных областях и разнятся лишь в низкочастотной областях при
w < 1/T1. Следует заметить, что чем больше значение постоянной времени Т1, тем больше диапазон частот, где ЛАХ исследуемой и эталонной систем совпадают, тем ближе по характеру переходные процессы в исследуемой системе к эталонным процессам.Уподобим рассматриваемую систему с П-регулятором в диапазоне частот
w М ( 1/T1, Ґ) системе с ПИ-регулятором, время изодрома которого выбрано из условия компенсации постоянной времени Т1, т.е. Ти=Т1. Тогда в выражении для передаточной функции разомкнутой исследуемой системы следует принятьК
0= Т1/2 ТmСледовательно, петлевой коэффициент передачи контура с П-регулятором, настроенным на технический оптимум (при Т
1>> Тm ) зависит только от отношения большой постоянной времени Т1 к сумме малых постоянных времени Тm.Переходные процессы по характеру и времени близки к стандартным. Однако статические характеристики замкнутого контура с П-регулятором будут отличаться от стандартных, характерных для систем, оптимизированных с использованием И- или ПИ- регуляторов.
Статические и динамические характеристики оптимизированного контура
Передаточная функция замкнутого контура с П-регулятором, настроенного на технический оптимум имеет вид
 ,
,
Статический коэффициент передачи контура меньше единицы и определяется выражением
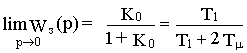
Этот коэффициент зависит только от соотношения постоянных времени Т
1 и Тm и приближается к единице при Т1 /Тm ® Ґ .Наличие статической ошибки регулирования определяет и отличие переходной характеристики замкнутого контура (реакции на единичный скачок задающего воздействия) от эталонной. Эти характеристики приведены на рисунке 20.3, где 1-истинная кривая, а 2- экспоненциальное приближение эталонной кривой.

Рис.20.4
Передаточная функция оптимизированного контура по возмущению -статическому моменту- может быть составлена с использованием следующей структурной схемы

Рис.20.5
которая после известных структурных преобразовании принимает вид

Рис.20.
6Заменяя замкнутый контур эквивалентным апериодическим звеном первого порядка, запишем выражение для передаточной функции оптимизированного контура по возмущению в виде
W
в(p)=w 1(p)/Mc(p)=-Следовательно, при Мс=Const операторное изображение выходной величины (скорости) имеет вид
w
1(p)= -Находя предел
![]() ,
,
установим, что он не равен нулю, и следовательно, регулируемая величина- скорость- в установившемся режиме содержит ошибку, обусловленную статическим моментом нагрузки. Эта ошибка равна
-
Dw = Мс/ b (1+К0),что согласуется с результатом, полученным при исследовании меха-нических характеристик указанной системы. Эта ошибка прямо про-порциональна статическому моменту Мс и обратно пропорциональна жесткости механической характеристики замкнутого контура
b
ск= b (1+К0)= b (1+Т1/2Тm)Как видно, увеличение жесткости в замкнутой системе по ставнению с ее значением в разомкнутой системе ограничено отношением постоянных времени (Т
1/2Тm). Увеличение коэффициента передачи Кп с целью увеличения жесткости механических характеристик приведет к увеличению колебательности кривой процесса относительно эталонной кривой.Найдем реакцию контура на скачок момента Мс при нулевых начальных условиях.
w
1(t)= L-1{-или
w
1(t)= -Dw L-1{Используя формулу разложения, легко находим
w
1(t)= -Dw (Временные зависимости, соответствующие полученной формуле представлены на рисунках 20.7а,б.
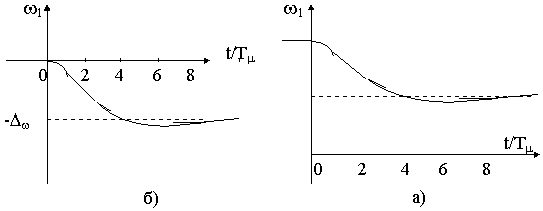
Рис.20.7
Выводы:
1. И статические и динамические характеристики системы практически полностью определяются соотношением постоянных времени Т
1 и Tm2. Длительности переходных процессов как по управлению, так и по возмущению одинаковы и равны
» 6(Тэ+ Тпр)3. Система обладает статической ошибкой и по управлению и по возмущению, определяемой типом регулятора и соотношением постоянных времени Т
1 и Tm