ЛЕКЦИЯ 2
Векторно-матричные математические модели ЭМС
При исследовании систем управления с научными или инженерными целями в большинстве случаев приходится иметь дело с двумя типами задач, К первому типу можно отнести задачи анализа, когда требуется определить характеристики заранее заданной системы. Ко второму типу- задачи синтеза, когда требуется спроектировать систему, обладающую заданными характеристиками. Существует два основных подхода к анализу и синтезу линейных систем управления.
Первый подход сводится, по существу, к составлению блок схемы системы или структурной схемы и определению передаточных функций отдельных элементов и всей системы.
Второй подход основан на возможности описания поведения системы некоторым количеством уравнений первого порядка относительно переменных состояния с начальными условиями. Методы анализа и синтеза систем управления, использующие этот способ описания поведения системы, принято называть методами пространства состояния. Этот подход лежит в основе современной теории управления.
Понятие “состояние”, лежащее в основе современного подхода к описанию поведения ЭМС, было впервые введено Дъюрингом в 1936 году. Начало широкому использованию этого подхода для решения задач ТАУ положили в 40-х годах Российские ученые Айзерман, Фельдбаум, Летов, Лурье.
При анализе и синтезе систем все переменные, характеризующие систему или имеющие к ней прямое отношение делятся на
входные переменные, представляющими собой управляющие и возмущающие воздействия ui, выходные переменные Xi, характеризующие реакцию системы и предсталяющие интерес для исследователя и промежуточные переменные Yi или переменные состояния, характеризующие динамическое поведение исследуемой системы (см. рис. 2.1).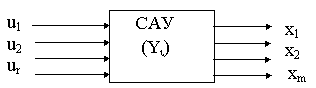
Рис.2.1
Для удобства оперирования с многомерными величинами совокупность входных переменных представим в виде вектора входа
UT
=[u1 u2 ....ur],совокупность выходных переменных - в виде вектора выхода
XT
=[x1 x2 ....xm],и совокупность переменных состояния- в виде вектора состояния
YT
=[y1 y2 ....yn].В любой момент времени t состояние системы является функцией начального состояния
Y(t0) и вектора входа U(t 0, t), т.е.Y
(t)= F[ Y(t0), U(t0,t)],где
F- однозначная функция своих аргументов.Вектор выхода в момент времени t является также функцией
Y(t0) и U(t 0, t) и может быть записан какX
(t)= Y [ Y(t0), U(t0,t)].Уравнения 2.1 и 2.2 называются уравнениями состояния системы. Для систем, описываемых дифференциальными уравнениями, уравнения 2.1 и 2.2 могут быть записаны в следующей общей форме
dY(t)/dt= F*[ Y(t0), U(t0,t),![]() (2.3)
(2.3)
dX(t)/dt=
Y *[ Y(t0), U(t0,t)].Если система описывается линейными дифференциальными уравнениями с постоянными коэффициентами, то уравнения состояния системы сводятся к следующим:
dY/dt=AY+BU, ![]() (2.5)
(2.5)
X=CY+DU,![]() (2.6)
(2.6)
где
A
- квадратная матрица размером nxn, называемая матрицей системы и. характеризующая динамические свойства системы;B
-прямоугольная матрица размером nxr, называемая матрицей управления. Она характеризует воздействие входных переменных ui на переменные состояния yi .C- матрица измерения размера mxn. Она характеризует связь выходных координат xi ( как правило это измеряемые переменные) с переменными состояния yi.
D- матрица размера mxr, характеризующая непосредственное воздействие входов u i на выходы x i
Вывод уравнений состояния является исходным моментом анализа и синтеза систем в современной теории управления ЭМС.
В качестве примера рассмотрим электродвигатель постоянного тока с независимым возбуждением, конструктивными постоянными Cе и Cм
, моментом инерции ротора J, моментом нагрузки на валу Мс , управляемый по цепи якоря изменением напряжения uя. Двигатель описывается двумя уравнениями: уравнением равновесия напряжений в цепи якоряu
я =L я di я /dt + Rя i я + Cе wи уравнением равновесия моментов на валу (уравнением Ньютона)
Jd
w /dt= Cм i я - МсРазрешив эти уравнения относительно производных, получим
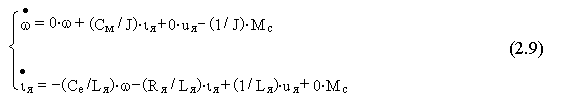
Примем в качестве переменных состояния скорость вращения ротора y
1=w и ток якоря y2 =i я ДПТ, а в качестве выходной переменной – противо ЭДС двигателя x1 = Cе w . Приводя систему (2.9) к матричной форме (2.5) и (2.6), получим
Полученные формулы 2.10-2.12 представляют собой векторно-матричную математическую модель двигателя постоянного тока .
Составим далее векторно-матричную модель механической системы, состоящей из груза с массой m, подвешенного на пружине с коэффициентом упругости k и двигающегося в цилиндре с коэффициентом трения f под действием управления u(t) - внешней силы (см. рис. 2.2 ).
Дифференциальное уравнение, описывающее поведение системы имеет вид
m d2z/dt2 +f dz/dt + kz=u(t) ![]() (2.14)
(2.14)
Примем в качестве переменных состояния -линейное перемещение груза y
1=z и линейную скорость перемещения груза y2=dz/dt.Тогда имеем y
2=dy1/dt и d2z/dt2 = dy2/dt.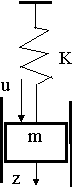
Рис.2.2.
В качестве выходной переменной x
1 примем линейное перемещение груза z, т.е. x1= y1=z. Следовательно, с учетом введенных обозначений уравнение (2.14) можно представить системой уравнений состояния вида
Записывая систему (2.15) в матричной форме (2.5)-(2.6), получим векторно-матричную модель рассматриваемой механической системы в виде
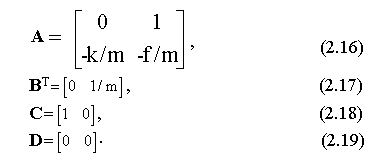
ПЕРЕДАТОЧНЫЕ МАТРИЦЫ СИСТЕМ
Научившись составлять векторно-матричные уравнения в форме переменных состояния, теперь необходимо выяснить, как эти уравнения и соответствующие им матрицы связаны с уже известными понятиями передаточной функции, характеристического уравнения и т.д.
С этой целью применим преобразование Лапласа при нулевых начальных условиях к уравнениям состояния системы в форме (2.5). Тогда
pY(p) = AY(p) +BU(p)
X(p)= CY(p)
Теперь вместо векторных переменных
Y(t), U(t) и X(t), являющихся функциями времени, мы имеем дело с их изображениями в области комплексной переменной p; в то же время A, B и C-матрицы соответствующих размеров с постоянными элементами остаются неизменными.В первом уравнении перенесем
AY(p) в левую часть и использовав соотношение pY(p)= p1Y(p) (где 1- единичная матрица размером nxn), представим первое уравнение в виде(p1- A) Y(p)= BU(p)
Отсюда
Y
(p)= (p1- A)-1 BU(p)и следовательно
X
(p)= C(p1- A)-1 BU(p)Вводя обозначения
G
(p)=(p1- A)-1 B, H(p)= C(p1- A)-1 B,запишем
Y
(p)= G(p) U(p), X(p)= H(p)U(p) (*)Матрица
H(p) размером mxr (т.к. X(p) это-вектор размера m, U(p)-вектор размера r) называется передаточной матрицей вход -выход системы. Элемент Hij этой матрицы представляет собой обычную передаточную функцию от j-го входа к i-му выходу. Это сразу становится ясным, если выписать отдельно i-ю строку равенства (*), предварительно выполнив умножение на U(p)xi(p)=Hi1(p) u1(p) +....+Hij(p) uj(p) +....+Hir(p) ur(p)
Если система имеет один вход и один выход (m=r=1), то передаточная функция вырождается в обычную передаточную функцию. В этом случае можно написать
H(p)= X(p)/ U(p)
В многомерном случае эта запись недопустима, т.к. операция деления на вектор не имеет смысла.
Матрица
G(p) размером nxr называется передаточной матрицей вход- состояние.Найдем передаточную матрицу
H(p) для рассмотренного выше двигателя постоянного тока. Предварительно вспомним, что операция обращения некоторой квадратной матрицы Ф может быть выполнена по формуле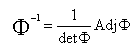
где присоединенная матрица T
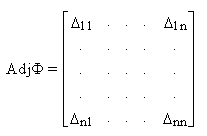
получается из матрицы Ф заменой каждого элемента
j ij его алгебраическим дополнением D ij с последующим транспонированием полученной матрицы.Для рассмотренного ДПТ имеем
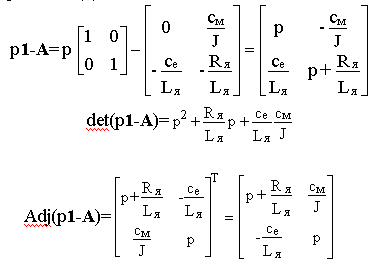
Следовательно
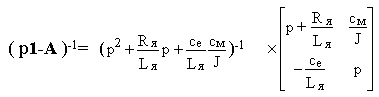
Отсюда
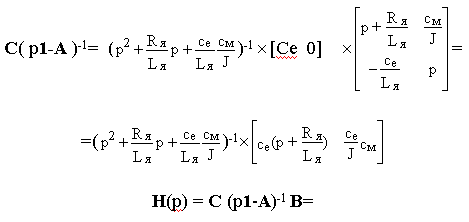
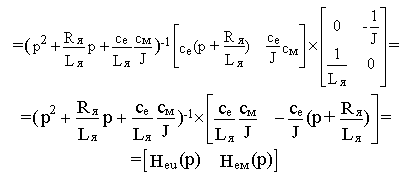
Первый и второй элементы полученной матрицы представляют собой соответственно передаточные функции “ЭДС- напряжение на якоре” и “ЭДС-момент нагрузки”. Вводя обозначения
|
|
(постоянная времени цепи якоря) и |
|
|
электромеханическая постоянная времени ДПТ, |
окончательно получим
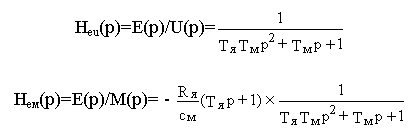
Так как в передаточные матрицы
G
(p)=(p1- A)-1 Bи
H
(p)= C(p1- A)-1 B,входит выражение (p
1- A)-1, то все элементы этих матриц, т.е. передаточные функции системы, содержат выражение det(p1-A), являющееся характеристическим полиномом системы. Корни этого полинома называются собственными числами матрицы A.