lec19

Лекция 19

Одноконтурная система с ПИ-регулятором скорости

Такие системы находят применение в тех случаях, когда Т_м>10Т_э, Т_пр<< Т_э и по техническим требованиям недопустимы статические ошибки по задающему и возмущающему воздействиям.

Исходная структурная схема системы имеет вид

Рис.19.1

Математическая модель в переменных состояния

Дополним систему уравнений состояния разомкнутой электромеханической системы

T_пр dw₀/dt= K_пр u_у - w₀

T_э dM/dt = b (w₀-w₁) - M,

JS dw₁/dt= M- M_c

уравнением замыкани e = u_зад - К_ww₁и системой уравнений, описывающих ПИ-регулятор. Поскольку структурная схема последнего имеет вид

Рис.19.2

где e - ошибка системы и y_и -выходной сигнал интегратора регулятора, систему уравнений регулятора запишем как

dy_и/dt= e ; u_у= К_п e +(К_п/T_и) y_и

или с учетом уравнения замыкания dy_и/dt= u_зад - К_ww₁;

Тогда после преобразований система уравнений состояния примет вид

T_пр dw₀/dt= - w₀- К₀w₁+ (К₀/К_w T_и) y_и+K₀ w_зад

T_э dM/dt = b w₀ - M- b w₁,

JS dw₁/dt= M- M_c

dy_и/dt= - К_ww₁ + К_ww_зад;

Для установившегося режима M= M_c и w₁ = w_зад

Следовательно, в установившемся режиме при постоянном зада-ющем и возмущающем воздействиях статическая ошибка принципиально равна нулю независимо от параметров звеньев системы и от величины внешнего возмущения М_с, т.е. w₁=w_зад.Значит механические характеристики указанной системы будут иметь следующий вид

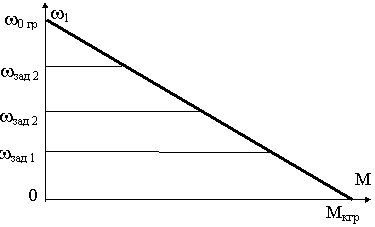
Рис.19.3

Принимая в качестве вектора состояния вектор Y^т = [w₀M w₁y_и]

и в качестве вектора управления - вектор U^т=[w_зад M_c ], запишем полученную систему в стандартной матричной форме

где

A=; B=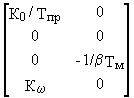

Оптимизация одноконтурной системы с ПИ-регулятором

После преобразований, структурную схему системы изобразим в следующем виде

Рис.19.4

Передаточная функция последнего звена представляет собой передаточную функцию линеаризованного ЭМП по моменту (возму-щению). При Т_м>4 Т_э, как было установлено ранее, последняя может быть представлена в виде

Ww _{1, Mc}(p) = ,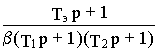

где Т₁ и Т₂- постоянные времени, определяемые корнями полинома знаменателя передаточной функции

а именно Т₁= mod (1/l₁) и Т₂= mod (1/l₂). Обратим внимание на то обстоятельство, что T₁>T₂ и при Т_м>>Т_э Т₁®Т_м и Т₂®Т_э.

Cледовательно, расчетную структурную схему системы можно изобразить в виде

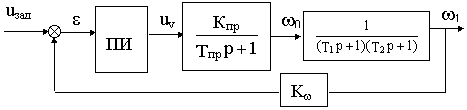
Рис.19.5

Заменим 2 инерционных звена с малыми (относительно Т₁) постоянными времени (преобразователь и апериодическое звено с постоянной времени Т₂) одним эквивалентным звеном с суммарной постоянной времени Т_m =Т_пр+ Т₂ . Тогда

W_р(p)=w₁(p)/ w_зад(p)=

Последняя передаточная функция соответствует эталонной передаточной функции разомкнутой системы, настроенной на технический оптимум

если,

а) Т₁, т.е. Т_и=Т₁.

б) 2Т_m = Т_и/ K₀или К₀= Т₁/2Т_m .

Следовательно, значение петлевого коэффициента усиления определяется соотношением постоянных времени Т₁/2Т_m. При этом коэффициент передачи ПИ-регулятора определяется выражением

К_п= Т₁/2Т_m К_пр К_w

Переходные процессы по управлению по характеру и времени соответствуют стандартным.

Исследуем далее реакцию контура на возмущение в виде момента. Для этого преобразуем структурную схему следующим образом:

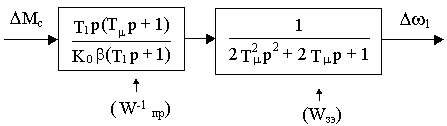
Рис.19.6

После подстановки К₀= Т₁/2Т_m получим

W_в(p)=D w ₁(p)/D M_c(p)=-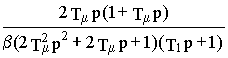

Находя предел ,

установим, что он равен нулю, и следовательно, регулируемая величина- скорость- в установившемся режиме не содержит ошибки, обусловленной статическим моментом нагрузки .

Найдем реакцию контура на скачок момента D М_с при нулевых начальных условиях.

Dw₁(t)= L^-1{-(D M_c/p) }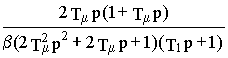

Используя формулу разложения, находим

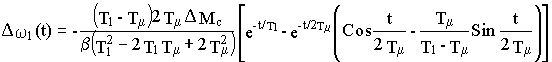
(19.1)

Временная зависимость, соответствующая полученной формуле (19.1) представлена на рис. 19.7.

Рис. 19.7

Анализ ее показывает, что время парирования возмущения равно времени переходного процесса по управлению, т.е. t_п @ 3 Т₁

Для приближенной оценки максимального значения динамического отклонения скорости Dw_макс примем, что оно имеет место в момент времени t*@ p Т_m, что соответствует четверти периода свободных колебаний скорости

Т_св=2p /w_св=4p Т_m.

Подставляя значение t* в формулу 19.1, получим

При Т_m < 10Т₁ без большой погрешности можно пользоваться для оценки максимального динамического отклонения скорости следующим соотношением

Выводы:

1.Статические и динамические одноконтурной системы с ПИ-регулятором относительно управляющего воздействия полностью соответствуют характеристикам эталонной системы, настроенной на технический оптимум, в предположении что малая некомпенсированная постоянная времени Т_m =Т_пр+ Т_{2 .}Быстродействие контура при этом практически определяется электрической постоянной времени Т_э, т.е. t_п @ 6 Т_э .

2. Система не имеет статической ошибкой и по управлению и по возмущению независимо от ее параметров, что определено типом регулятора

3. Длительности переходных процессов по возмущению опреде-ляется самой большой постоянной времени Т_1@Т_м ,т.е. t_п @ 3 Т_м

4. Динамические отклонения скорости в процессе парирования скачкообразного изменения момента нагрузки прямо пропорциональны величине скачка DМ_с и некомпенсированной постоянной времени Т_m и обратно пропорциональны жесткости механических характеристик собственно ЭМП и большой постоянной времени Т₁.