РЕГУЛИРОВАНИЕ СКОРОСТИ В СИСТЕМЕ “УПП-ЭМП”

Лекция 18

Технологические режимы многих производственных механизмов на разных этапах работы требуют движения исполнительного органа с различной скоростью. Это обеспечивается либо механическим путем, либо путем электрического регулирования скорости.

Механические способы требуют введения в кинематическую цепь системы коробок передач или других устройств, усложняющих механическую подсистему ЭМС и снижающих ее надежность.

Этого недостатка лишен второй путь- электрическое регулирование скорости с целью поддержания ее на заданном уровне или изменения ее во времени по требуемым законам с заданной точностью. Именно этим путем в современном электроприводе обеспечивается плавное регулирование скорости в диапазоне w _макс/w _мин до 100000 . Вопросы организации систем автоматического регулирования скорости и рассматриваются в данном разделе.

Требования к системам регулирования скорости

Рассмотрим обобщенную разомкнутую электромеханическую систему с известной структурной схемой

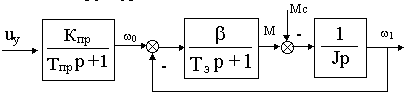
Рис.18.1

Структура описывается системой уравнений состояния

T_пр dw₀/dt= K_пр u_у - w₀

T_э dM/dt = b (w₀-w₁) - M,

JS dw₁/dt= M- M_c

В установившемся режиме, когда все производные равны нулю, запишем систему так

0= K_пр u_у - w₀

0= b (w₀-w₁) - M,

0= M- M_c

Исключая последовательно переменные, получим уравнение семейства механических характеристик в виде

w₁ = K_пр u_у- М_с/ b

или

w₁ = w_х - D_w(M),

где w_х = K_пр u_у- скорость холостого хода , пропорциональная сигналу управления и D_w(M)- отклонение скорости от w_х, обусловленное наличием статического момента нагрузки на валу М_с. Семейство механических характеристик представлено на рис.18.2.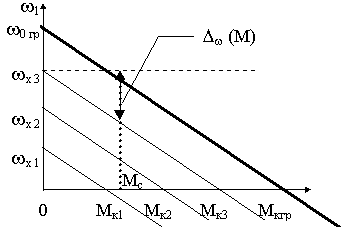

Рис.18.2

С ростом сигнала управления u_у возрастает скорость холостого хода и механическая характеристика смещается вверх по оси скоростей параллельно самой себе (w_х1<w_х2<w_х3).

Рост момента нагрузки приводит к отклонению скорости от заданного значения w_хтем в большей степени, чем ниже значение жесткости механической характеристики b. Результирующая скорость падает с ростом момента нагрузки в двигательном режиме работы ЭМП и растет- в генераторном режиме (если таковой обеспечивается схемой электрического преобразователя). Иными словами, при регулировании скорости момент нагрузки оказывается сильным возмущением и с точки зрения регулирования скорости необходимо искать методы, позволяющие повышать модуль статической жесткости b .

Однако, бесконечно большое увеличение сигнала управления не приводит к такому же возрастанию скорости w_х, которую мы будем принимать условно за заданное значение скорости в системе регулирования скорости. Причиной является ограничение выходного сигнала электрического преобразователя на уровне w_0гр. Следовательно, максимальное значение заданной скорости ограничено на уровне w_0гр. Этому значению соответствует предельная механическая характеристика

w₁ = w_{0 гр} -М_с/ b ,

выделенная на рис. жирной линией.

Таким образом идеальной системой с позиции регулирования скорости следовало бы считать систему, у которой

а) механическая характеристика была бы параллельна оси моментов (см. кривую на рис.), что означает, что скорость вращения не зависит от момента нагрузки

б) статическая регулировочная характеристика w_х(u_у) была бы линейной в диапазоне 0 <w_х< w_{0 гр}

в) реакция системы на скачки управляющего u_уи возмущающего М_своздействий должна быть по возможности мгновенной ( динамические качества системы должны быть высокими)

В системе с управлением ЭМП от электрического преобразователя указанная цель может быть достигнута введением отрицательной обратной связи по скорости на вход управляемого преобразователя в соответствии со структурной схемой, приведенной на рис.18.3.

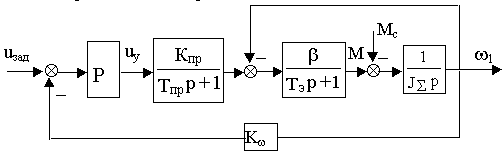
Рис.18.3

Механические характеристики системы “УПП-ЭМП” с отрицательной обратной связью по скорости и П-регулятором

Представим управляющее воздействие u_у на входе электрического преобразователя в виде разности

u_у= K_п(u_зад - К_ww₁),

где u_{зад -}сигнал, пропорциональный заданному значению скорости ,

К_w - коэффициент, характеризующий глубину отрицательной обратной связи по скорости.

Тогда, систему уравнений состояния можно переписать в виде

T_пр dw₀/dt= - w₀- K_пр K_п К_ww₁ + K_пр K_п U_зад

T_э dM/dt = b w₀- M- b w₁,

JS dw₁/dt= M- M_c

Для установившегося режима система принимает вид

0=- w₀- K_пр K_п Кw _{w 1} + K_пр K_п U_зад

0 = b w₀- M- b w₁,

0= M- M_c

Последовательно, начиная с последнего уравнения, исключая переменные, находим выражение, определяющее статическую механическую характеристику искомой системы

После введения понятий петлевого коэффициента усиления

К₀=K_пр K_пК_w

и заданного значения скорости w_1зад= u_зад/К_w уравнение механических характеристик примет вид

Приводя как и ранее данное уравнение к виду

w₁ = w_1х- D_w(М)_,

получим, что

- скорость холостого хода w_1х пропорциональна сигналу задания и его значение приближается к заданному значению w_1зад с ростом петлевого коэффициента усиления К₀

- отклонение скорости под воздействием статического момента D_мтакже падает с ростом коэффициента передачи К₀в одинаковом диапазоне изменения момента, т.е. возрастает эквивалентная жесткость механических характеристик. Вводя обозначение

b_{э ск}=b (1+К₀)

получим D_w = М_с/b_эск,где b_эск-жесткость механических характеристик замкнутой по скорости системы. Как видно, с ростом петлевого усиления К₀ жесткость механических характеристик системы возрастает и при К₀ ® Ґ b _эск® Ґ.

Семейство механических характеристик системы с отрицательной обратной связью по скорости, соответствующее одному заданному значению скорости w_1зад и трем различным значениям петлевого коэффициента усиления К₀₁ <К₀₂ <К₀₃представлено на рис.18.4. прямыми соответственно 1,2 и 3.

Рис.18.4

Легко показать, что отрицательная обратная связь по скорости оказывает форсирующее действие на замедленные инерцией электромеханические процессы в системе. Последние, как нам уже известно, во многом определяются электромеханической постоянной времени Т_м=Jе / b, обратно пропорциональной жесткости механических характеристик b. Увеличение петлевого усиления К₀ приводит к уве-личению эквивалентной жесткости механических характеристик b_ск и как следствие, к снижению значения электромеханической постоянной времени, в тех случаях, пока выходное напряжение управляемого преобразователя в переходных процессах не выходит на уровень ограничения.

Однако беспредельное увеличение К₀ с целью повышения жесткости механических характеристик при наличии электромагнитной инерции ЭМП и электрической инерции управляемого преобразователя может привести к росту колебательности переходных процессов и в конце концов к потере устойчивости системы регулирования скорости. Поэтому вопросы оптимизации контуров регулирования при достижении заданных точностных показателей и здесь является актуальными.