Лекция 17

УНИФИЦИРОВАННЫЙ КОНТУР РЕГУЛИРОВАНИЯ МОМЕНТА

Беспредельное увеличение петлевого усиления в системе с отрицательной обратной связью по моменту, рассмотренной выше, с целью снижения жесткости механических характеристик, неизбежно приведет к возрастанию колебательности переходного процесса и в конце концов к потере устойчивости системы, что потребует, естественно, принятия мер по динамической коррекции системы. Эта проблема легко решается введением ПИ-регулятора в прямой канал контура и настройкой его на технический оптимум. Таким образом и строятся унифицированные контура регулирования момента.

Структурная схема и математическая модель контура

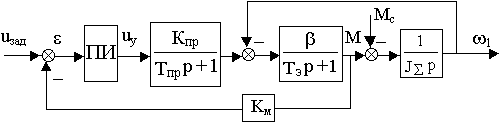
Рис.17.1

Математическую модель контура образуют уже известные уравнения обобщенной энергетической подсистемы ЭПС

Tпр dw0/dt= Kпр uу - w0

Tэ dM/dt = b (w0-w1) - M,

JS dw 1/dt= M- Mc

уравнение замыкания e = uзад - Км М

и уравнения ПИ-регулятора момента. Последние получим, используя детализированную структурную схему регулятора (рис.17.2)

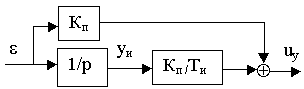
Рис.17.2

где e - ошибка системы и yи -выходной сигнал интегратора регулятора. Систему уравнений регулятора запишем в виде

dyи/dt= e ; uу = Кп e +(Кп /Tи) yи.

 

Статические характеристики контура

Анализируя уравнения регулятора, легко установить, что в устано-вившемся режиме при постоянных задающем и возмущающем воз-действиях статическая ошибка принципиально равна нулю независимо от параметров звеньев системы и от величины внешнего возмущения w1, т.е.

М=Мзад =Uзад/Км

Графики статических регулировочных и механических характеристик контура изображены соответственно на рис. 17.3 и 17.4

Рис.17.3

Рис.17.4

Заметим, что в данной системе с ПИ-регулятором нулевая жесткость механических характеристик и статическая ошибка обеспечена структурно и независимо от конкретных параметров электрического преобразователя, двигателя и регулятора. Варьируя последними можно изменять быстродействие и качество переходных процессов, также как и динамические ошибки по управлению и возмущению, не влияя на характеристики установившегося режима.

 

Опитимизация контура регулирования момента

Как было показано выше, при регулировании момента электро-механическая связь является возмущающим воздействием, снижающим точность регулирования. Поскольку в системе с отрицательной обратной связью по моменту влияние этой связи в значительной степени ослаблено, разомкнем эту связь при синтезе контура регулирования, пренебрегая ее влиянием на динамику контура в процессах по управлению. Влияние этой связи на динамическую точность регулирования в дальнейшем будем оценивать, считая изменения скорости независимым возмущающим водействием {f(t)= w1}. Структурная схема контура примет при этом вид рис.17.5

Рис.17.5

Настроим контур на технический оптимум, используя ПИ-регулятор. Поcкольку обычно Тэ>>Тпр и, кроме того, инерционность преобразователя по условию компенсировать нельзя и не имеет смысла, то примем постоянную времени преобразователя в качестве малой некомпенсированной постоянной (Тпр=Тm1) и выберем время изодрома регулятора из условия компенсации постоянной времени Тэ, т.е. Ти=Тэ Тогда передаточная функция разомкнутого внутреннего контура примет вид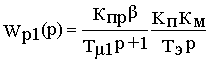

Оптимизируя контур, найдем

2Tпр = Тэ/ Кпр Кп Кмb ® Кп =Тэ / 2Кпрb Tпр Км

Передаточная функция замкнутого контура регулирования момента примет вид

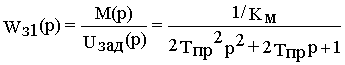
или

Характер переходного процесса соответствует стандартному, а время процесса составляет величину » 6 Тпр.

 

 

 

ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ КОНТУРА

 

Реакция контура на скачок задающего воздействия при заторможенном роторе ЭМП соответствует расчетной. Изменение скорости ЭМП (возмущающего воздействия для контура тока) из-за наличия электромеханической связи вызывают отличие реального переходного процесса от расчетного. Выражение, определяющее переходный процесс по управлению в контуре тока при наличии электро-механической связи в ЭМП получается достаточно громоздким, а вывод его - трудоемок. Поэтому мы оценим здесь влияние электромеханической связи на переходный процесс приближенно

Влияние динамического возмущения на переходный процесс по управлению можно оценить, зная передаточную функцию оптимизированного контура по возмущению.

Wв(p)= M(p)/w1(p)= Wзэ(p)/WR(p)Wпр(p)=

С учетом того, что Кп =Тэ / 2Кпрb Tпр Км , последнее выражение приведем к виду

Wв(p)=

или после замены оптимизированного контура эквивалентным апериодическим звеном

Wв(p)=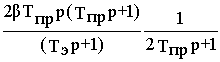

Реакция оптимизированного контура на скачкообразное возмущение не представляет интереса, поскольку возмущением является скорость w1, а последняя принципиально скачком изменяться не может. Характерными для контура являются возмущения по характеру гармонические (особенно при наличии упругих связей в механической подсистеме) или изменяющиеся во времени по закону, близкому к линейному.

Реакцию контура на возмущения синусоидального характера можно оценить по частотной характеристике. ЛАЧХ, соответствующей полученной передаточной функции Wв(p). При Тэ>>2Тпр (что выполняется практически всегда) ЛАЧХ имеет вид, представленный на рис.17.6.

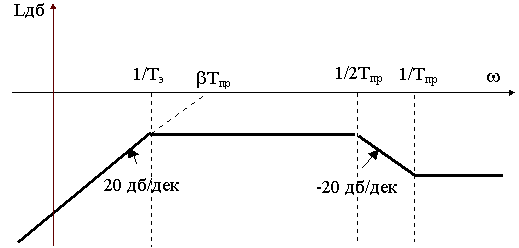
Рис.17.6

Как видно, наибольшим коэффициентом передачи обладает канал w1 ® М в диапазоне частот w М (1/Тэ, 1/2 Тпр) и поэтому наибольшее влияние на динамическую точность регулирования момента оказывают механические колебания с частотами, расположенными в указанной полосе.

Проанализируем далее влияние линейно-изменяющегося во времени возмущения w1(t)= e t на реакцию контура на скачкообразное изменение управляющего воздействия Мзад при нулевых начальных условиях.

Используя принцип суперпозиции найдем реакцию контура на одновременно действующие управляющее Мзад(t)=const и возмущающее w1(t)= et воздействия в виде суммы двух составляющих, т.е.

M(t)= X1(t) - X2(t).

Первая составляющая представляет собой стандартную реакцию оптимизированного контура на скачок управляющего (задающего) воздействия при отсутствии возмущения, т.е.

X1(t) = Мзад (1-е-t/2Тпр)

Вторая составляющая представляет собой реакцию оптимизи-рованного контура на возмущающее воздействие заданного вида при отсутствии задающего воздействия. Его мы найдем, используя пере-даточную функцию контура по возмущению, как

X2(t)= L-1{(e /p2)Wв(p)}

или

X2(t)= L-1 { }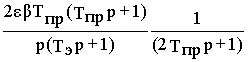

Находя

,

установим, что эта реакция содержит постоянную составляющую в виде моментной ошибки, пропорциональной скорости изменения возмущения e, жесткости механических характеристик ЭМП b и постоянной времени преобразователя Тпр. Далее эту ошибку мы будем обозначать как DМe.

Знаменатель изображения X2(p) имеет три корня: p1=0, p2=-1/Тэ и p3=-1/2Тпр. Используя формулу разложения, искомую реакцию можно найти в виде

X2(t)= DМe ,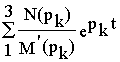

где N(p)= 1+Тпрp. M’(p)= 6 ТэТпрp2 + (4Тпр+2Тэ)p+1

Тогда

N(p1)= 1; M’(p1)= 1: N(p1)/M’(p1)= 1.

N(p2)= 1- Тпр/Тэ ; M’(p2)=2Тпр/Тэ - 1; N(p2)/M’(p2)=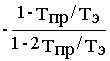

N(p3)= 1/2 ; M’(p3)= Тэ/2Тпр - 1; N(p3)/M’(p3)=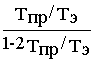

Следовательно,

X2(t)= D Мe -D Мe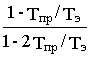 e -t/тэ +D Мe 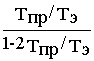e -t/2Тпр

и окончательно,

М(t) = (Мзад -D Мe ) -( Мзад +D Мe ) e -t/2Тпр

+D Мe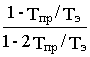 e -t/тэ

Временные зависимости X1(t), X2(t), М(t) и w1(t) приведены на рисунке 17.7 .

Рис.17.7

Анализируя полученные временные зависимости, можно заключить, что

- Линейно-возрастающее возмущение обуславливает появление статической ошибки DМe, пропрциональной скорости изменения возмущения,

- Время реакции в общем случае возрастает относительно расчетного (6 Тпр), поскольку определяется электрической постоянной времени Тэ>> 2Тпр

- Кривая M(t) приближается к кривой X1(t) с уменьшением ошибки DМe, пропорциональной Тпр, в том случае, если преобразователь безинерционный (Тпр =0).

- Время реакции равно расчетному (6 Тпр), если DМe Ј 0.05 Мзад