Лекция 15
Оптимизация каскадных систем управления
Системы подчиненного регулирования (каскадные системы управления)
В настоящее время при создании систем управления ЭМС широко применяется принцип последовательной коррекции или принцип подчиненного регулирования. Этот принцип состоит в следующем.
Объект регулирования представляется в виде последовательно соединенных звеньев Wоб1
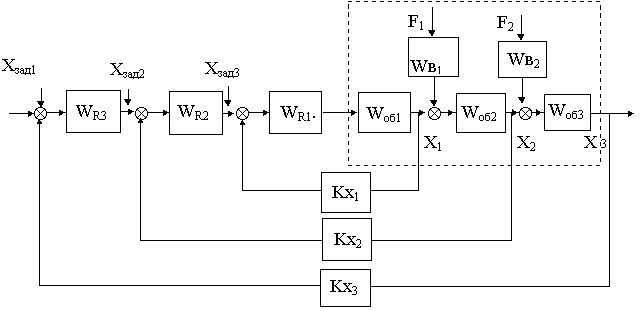
(p), Wоб2 (p), Wоб3(p) и т.д. с промежуточными координатами x1, x2, x3, ... и регулируемой (выходной) координатой X (см. структурную схему на рис.15.1. В качестве указанных координат используются существенные координаты, такие, например, как ток, напряжение, ЭДС, магнитный поток, момент, скорость, положение.Для управления каждой координатой организуется отдельный контур со своей обратной связью и своим регулятором. На рис. 15.1 датчики координат представлены звеньями с коэффициентами передачи Kx
1, Kx2 и Kx, а передаточные функции регуляторов обозначены через WR1, WR2, WR3.
Рис. 15.1.
Замкнутые контуры регулирования образуют систему, в которой имеется внутренний контур управления, состоящий из регулятора W
R1 первого звена объекта Wоб1 и цепи обратной связи по координате X1, первый внешний контур, включающий в себя внутренний контур , второе звено объекта Wоб2, регулятор WR2 и цепь обратной связи по координате X2 и второй внешний контур, включающий в себя первый внешний контур, третье звено объекта управления Wоб3 , регулятор WR3 и обратную связь по координате X3, для рассматриваемого случая являющейся регулируемой, т.е. X3=X.Выходной сигнал регулятора каждого внешнего контура является задающим для последующего, заключенного внутри него контура. Таким образом, каждый внутренний контур регулирования подчинен соответствующему внешнему.
Каскадные системы управления характеризуются лучшим качеством управления по сравнению с одноконтурными системами по следующим причинам:
- возмущения, F
1(p), F2(p), поступающие на части объекта, расположенные ближе к входу, прежде чем воздействовать на выходную координату X (регулируемую переменную) предварительно парируются во внутренних контурах управления;- наличие внутренних контуров уменьшает влияние изменения параметров входной части на динамические качества системы регулирования ( снижается чувствительность системы к изменению параметров объекта);
- поведение регулируемой переменной X становится более быстрым (менее инертным), если внутренний контур обеспечивает более быстрые собственные движения по сравнению с исходными.
Практическое преимущество разделения системы на контура с основными и вспомогательными регуляторами состоит в том, что настройку их параметров можно осуществлять независимо и последовательно. Она осуществляется следующим образом:
1.Настройка первого внутреннего контура осуществляется на оптимум по модулю .
2. При переходе к внешнему контуру передаточную функцию замкнутого внутреннего контура упрощают, аппроксимируя его апериодическим звеном первого порядка
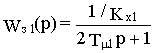
Новую некомпенсированную постоянную выбирают с учетом быстродействия внутреннего контура и датчиков обратной связи. Если постоянные времени последних действительно малы, то их практически можно не выделять из других постоянных времени.
Если во внешнем контуре есть свои малые постоянные, то эквивалентная постоянная времени замкнутого внутреннего контура 2Т
m1 входит в состав суммарной малой постоянной времени Тm2.Если во внешнем контуре нет своих малых постоянных времени, то для него некомпенсируемая постоянная времени Т
m2 выбирается равной 2Тm1.3. Заменяя первый внешний контур эквивалентным апериодическим звеном, аналогичным образом осуществляем оптимизацию второго внешнего контура и т.д.
Легко установить, что быстродействие каждого внешнего контура не менее чем в 2 раза ниже быстродействия подчиненного ему внутреннего контура.
К преимуществам системы подчиненного регулирования можно отнести
- простоту наладки и настройки (Каждый контур включает в себя регулятор, за счет придания которому определенных динамических свойств получаются стандартные характеристики. Настройку в процессе наладки ведут начиная с внутреннего контура. Поскольку регулятор имеет простую передаточную функцию, а качество настройки может быть легко оценено по результатам сравнения реакции контура на скачок управляющего воздействия со стандартной переходной характеристикой, наладка системы оказывается очень простой.)
- удобство ограничения предельных значений промежуточных координат системы ( поскольку выходной сигнал регулятора внешнего контура является заданным значением для внутреннего контура достигается за счет ограничений определенным значением выходного сигнала регулятора внешнего контура)
Недостаток - некоторый проигрыш по быстродействию, связанный с последовательным воздействием на объект через внутренние контура, а не сразу через входное звено объекта.
В большинстве случаев конкретного применения в ЭМС, указанный недостаток несуществен, а перечисленные выше преимущества имеют решающее значение .
ПРИМЕР: Построить систему подчиненного регулирования выходной координаты объекта со структурной схемой, представленной на рис.15.2

Рис. 15.2.
Сначала построим внутренний (подчиненный контур регулирования координаты X
1 по структурной схеме рис.15.3
Рис.15.3
Настроим контур на технический оптимум. Для этого используем ПИ-регулятор. Покольку Т
1 >> Tпр и кроме того инерционность преобразователя по условию компенсировать нельзя и не имеет смысла, то примем постоянную времени преобразователя в качестве малой некомпенсированной постоянной (Тпр=Тm1) и выберем время изодрома регулятора из условия компенсации постоянной времени Т1. Примем кроме того значение коэффициента передачи датчика координаты X1 равным Kx1 .Тогда передаточная функция разомкнутого внутреннего контура примет вид
Оптимизируя контур, найдем
2T
m1 = Т1/ К1 Кп Кx1 ® Кп =Т1 / 2К1Tm1 Кx1Передаточная функция замкнутого внутреннего контура примет вид
 ,
,
или после упрощения
 .
.
Заменив оптимизированный замкнутый внутренний контур апериодическим звеном, оптимизируем внешний контур, построенный по структурной схеме (рис. 15.4)
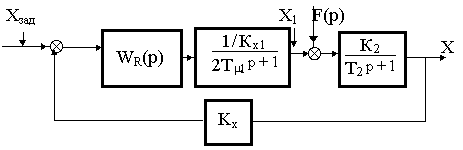
Рис.15.4
Для оптимизации внешнего контура применим ПИ-регулятор и выберем его настройки из условия обеспечения технического оптимума. Примем в качестве малой некомпенсированной постоянной - постоянную времени эквивалентного замкнутого внутреннего контура
- Tm2 =2Tm1 и выбрав время изодрома регулятора внешнего контура из условия компенсации инерционности второго апериодического звена ,т.е. Ти= Т2. Тогда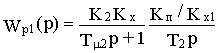
Оптимизируя контур, найдем
2T
m2 = Т2/ К2 Кx Кп /Кx1 ® Кп =Т2 Кx1 / 2К2Tm1 КxПередаточная фунция системы в окончательном виде
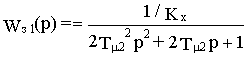 .
.
Эмпирический метод настройки Циглера-Никольса
В практике настройки замкнутых систем управления нередко встречается задача обеспечения приемлимых динамических качеств замкнутой системы с помощью регуляторов, обеспечивающих типовые линейные алгоритмы управления (П-, ПИ- или ПИД-) устойчивыми объектами, параметры которых точно измерить не удается. В этом случае результат можно получить, используя метод замкнутого контура Зиглера-Никольса. Метод состоит в следующем:
а) к выходу регулятора или объекта подключается самопишущий потенциометр, а интегральное и дифференциальное воздействия регулятора - блокируются (исключаются).
б) затем коэффициент пропорциональности регулятора Кп постепенно увеличивают, пока при некотором значении этого коэффициента Кп
пред в системе не установятся устойчивые колебания с периодом Т пред. ( см. рис. 15.5)
Рис.15.5
в) далее рассчитываются и устанавливаются параметры регулятора на основе следующих соотношений
Для П- регулятора Кп= 0.5 Кп
Для ПИ- регулятора Кп= 0.45 Кп пред, Ти= Т пред/1.2
Для ПИД- регулятора Кп= 0.6 Кп
пред, Ти= Т пред/2, Тд= Т пред/8