
ЛЕКЦИЯ 14
Реакция оптимизированных контуров на возмущающие воздействия
Реакции контуров, оптимизированных по одному критерию, на возмущающие воздействия, приложенные к различным точкам объекта в общем случае отличаются от реакций этих контуров на управляющие воздействия. Это можно легко показать на примере системы, структурная схема которой приведена на рис. 14.1

Рис. 14.1.
После преобразования эта структурная схема приводится к следующей
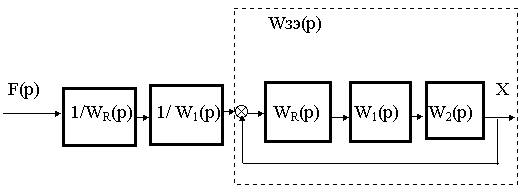
Рис. 14.2.
Передаточная функция контура по возмущению определяется выражением
W
в(p)= X(p)/ F(p)= Wзэ(p) /[WR(p) W1(p]
Как видно и время и характер реакции контура на возмущение зависит в общем случае как от параметров оптимизированного контура, так и от параметров объекта и регулятора. Рассмотрим несколько частных случаев.
1.Часто встречающий в практике проектирования систем управления ЭМС случай, когда входная часть объекта содержит апериодическое звено с передаточной функцией W
1(p) и принципиально некомпенсируемой постоянной времени Tm , а выходная часть представляет собой интегрирующее звено с передаточной функцией W2(p) , на входе которого действует возмущающее воздействие f(t).а) настроим контур на технический оптимум с использованием П-регулятора. Структурная схема разомкнутого контура имеет вид

Для настройки системы на технический оптимум необходимо выполнить условие Кп
=1/ 2K1 K2Tm .Тогда в соответствии с 14.1 передаточная функция системы по возмущению примет вид
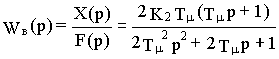 ,
, ![]() (14.2)
(14.2)
Анализируя полученное выражение , легко установить, что
- наличие возмущения приводит к появлению статической ошибки в контуре несмотря на наличие интегрирующего звена в канале f
® X,- величина динамической ошибки в процессе отработки возмущения зависит от соотношения коэффициента K
2 и величины некомпенсированной малой постоянной времени Tm ,- время переходного процесса соответствует эталонному процессу и равно 6 T
m .б) настроим контур на симметричный оптимум с использованием ПИ-регулятора. Структурная схема контура имеет вид
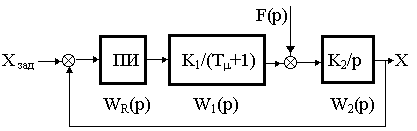
Рис. 14.4.
Для настройки системы на симметричный оптимум необходимо выполнить условия Кп
=1/ 2K1 K2Tm и Ти=4 TmПри этих условиях передаточная функция системы по возмущению примет вид
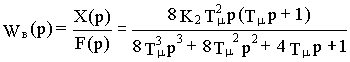 ,
, ![]() (14.3)
(14.3)
Анализируя полученное выражение , легко установить, что
- возмущение не приводит к появлению статической ошибки в контуре из-за наличия идеального дифференцирующего звена в числителе передаточной функции по возмущению ,
- величина динамической ошибки в процессе отработки возмущения зависит от соотношения коэффициента K
2 и величины некомпенсированной малой постоянной времени Tm ,- время переходного процесса определяется только малой некомпенсированной постоянной времени контура и не зависит от параметров объекта.
2. Рассмотрим случай, когда входная часть объекта содержит апериодическое звено с принципиально некомпенсируемой постоянной времени T
m, а выходная часть представляет собой апериодическое звено с постоянной времени Т2, на входе которого действует возмущающее воздействие f(t).Структурная схема контура имеет вид
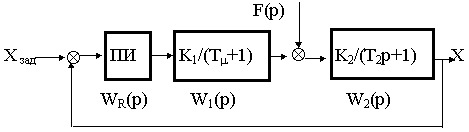
Рис.14.5.
Настроим контур на технический оптимум с использованием ПИ-регулятора. Для настройки системы на технический оптимум необходимо скомпенсировать инерционность второй части объекта, для чего выбираем Ти= Т
2 . Тогда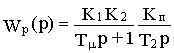
Условием оптимальной настройки, кроме Ти=Т
2 будет2T
m = Т2/ К1 К2Кп ® Кп =Т2 / 2Tm К1К2Тогда
1/ (WR(p) W1(p)) = 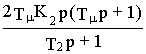
и следовательно,
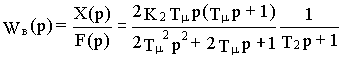 ,
,
Анализируя полученное выражение , легко установить, что
- наличие возмущения не приводит к появлению статической ошибки в контуре из-за наличия интегрирующего звена в прямом канале до места приложения возмущения (за исключением случая T
2 / Tm ® Ґ ),- величина динамической ошибки в процессе отработки возмущения зависит от соотношения коэффициента K
2, величины некомпенсированной малой постоянной времени Tm и постоянной времени T2- характер и время переходного процесса зависят от соотношения постоянных времени T
2 / Tm .Сглаживание задающего сигнала
Для переходной функции контура регулирования, настроенного на симметричный оптимум, характерен весьма заметный положительный выброс (перерегулирование), который может достигать 43,5%. Столь резкие колебания регулируемой величины в переходном процессе для электромеханических систем бывают допустимы только в редких случаях даже при резких изменениях или скачках задающей величины.
Числитель передаточной функции замкнутого оптимизированного контура

![]() (14.4)
(14.4)
характеризует некоторое упреждение, сходное с упреждением, например, ПД-регулятора. Это упреждением может быть скомпенсировано с помощью искусственно созданной инерционности -так называемого сглаживающего элемента. Этот элемент устанавливается на входе замкнутого контура, настроенного на “симметричный оптимум” в соответствии со структурной схемой (рис. 14.6 )и имеет передаточную функцию
 ,
, ![]() (14.5)
(14.5)
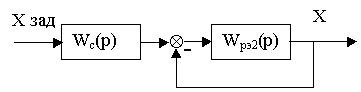
Рис.14.6.
При этом передаточная функция замкнутого оптимизированного контура вместе со сглаживающим звеном примет вид
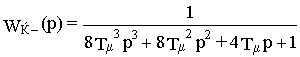
![]() (14.6)
(14.6)
Среди полюсов передаточной функции (корней полинома знаменателя) имеется один вещественный корень
p1= - 1/2 T
mи пара комплексно-сопряженных корней
p2,3= -1/4 T
m ± j(Ц 3/4 Tm )(Примеч: При нахождении корней целесообразно использовать разложение
1+8 T
m 3 p3= 1+(2 pTm )3= (1+2pTm )(1-2pTm +4Tm 2 p2)Находя переходную характеристику контура как
h(t)=L-1{W
з2с(p)/p},получим
h(t)= 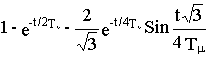
![]() (14.7)
(14.7)
Последнему выражению соответствует кривая 1 на рис.14.7. Кривая 2 на том же рисунке представляет переходную характеристику контура, настроенного на симметричный оптимум без сглаживающего фильтра на входе.
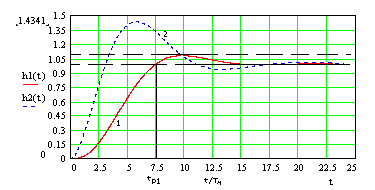
Рис.14.7.
Из графика видно, что время первого согласования для симметрично оптимизированного контура со сглаживающим звеном tр1
= 7.6 Tm .-время переходного процесса (время вхождения в область значений, отличающихся не более чем на 5% от установившегося значения равно
t
п= 12Tm .- перерегулирование
D
Xмакс= 8.1 %Если требуется до конца подавить перерегулирование, то постоянную времени сглаживающего звена выбирают равной 6T
m . Быстродействие контура при этом естественно снижается.Упрощенное описание оптимизированных контуров регулирования
В целом ряде случаев оптимизированный контур входит в состав сложной системы регулирования. Для того, чтобы по возможности упростить вид общей передаточной функции системы бывает целесо-образно подобрать для приближенного описания оптимизированного контура функцию первого порядка .
Передаточная функция контура, настроенного на технический оптимум имеет вид
 ,
, ![]() (14.8)
(14.8)
а переходная характеристика иллюстрируется кривой 1 на рис. 14.8.
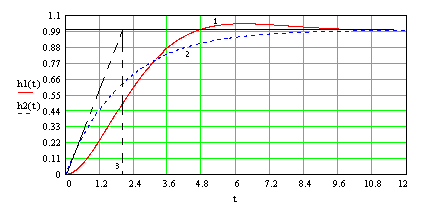
Рис.14.8.
Сравним эту передаточную функцию и соответствующую ей переходную характеристику с соответствующими характеристиками апериодического звена вида
![]()
![]() (14.9)
(14.9)
Переходная характеристика этого звена представлена кривой 2 на том же рисунке. Она представляет собой экспоненциальную огибающую эталонного слабоколебательного процесса и описывается выражением
![]()
![]() (14.10)
(14.10)
Отклонение кривой 1 от экспоненциальной огибающей 2 не очень велико. Время переходного процесса одинаково и равно tп
= 6Tm . Кроме того, положительная и отрицательная площади кривых “отклонение - время” равны друг другу. Поэтому не впадая в большую ошибку можно считать апериодическое звено с передаточной функцией (14.9) эквивалентом оптимизированного контура по условиям технического оптимума контура.Рассуждая аналогично, можно контур, настроенный на симмет-ричный оптимум со сглаживающим звеном на входе и описываемый передаточной функцией

без большого ущерба для точности заменить эквивалентным аперио-дическим звеном первого порядка с постоянной времени 4T
m , т.е.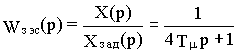
![]() (14.11)
(14.11)