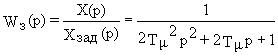lec13

ЛЕКЦИЯ 13

Приемы и методы оптимизации

линейных контуров регулирования

Настройка на “технический оптимум”

Передаточной функцией вида

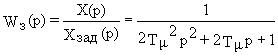, (13.1)

соответствующей контуру, настроенному на технический оптимум, описывается система, имеющая в прямом канале звено с передаточной функцией

(13.2)

и охваченное единичной обратной связью с выхода на вход этого звена. ЛАЧХ эталонной разомкнутой системы имеет следующий вид

Рис. 13.1.

Если имеет место последовательная коррекция контура и регулятор с передаточной функцией W_R(p) включен последовательно с объектом, обладающим передаточной функцией W_об(p), то контур будет настроен на технический оптимум, если выполняется условие

W_рэ1(p)= W_R(p) W_об(p), (13.3)

Таким образом, оптимизация практически состоит в пригонке передаточной функции прямого канала оптимизируемой системы к эталонному виду путем выбора подходящего типа регулятора и его настроек. Поскольку такого рода оптимизация для объекта первого порядка теряет смысл, мы рассмотрим приемы оптимизации для статических объектов второго и более высоких порядков.

Примем, что передаточная функция объекта регулирования имеет вид

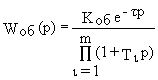, (13.4)

где t - постоянное запаздывание, а T_i - постоянные времени элементов объекта, расположенные в порядке убывания по значению и рассмотрим несколько частных случаев.

1. Объект содержит ряд апериодических звеньев первого порядка постоянные времени объекта - соизмеримы и t _з=0.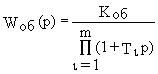

В этом случае оптимизация контура проводится с использованием И-регулятора. Передаточная функция разомкнутого контура при этом записывется в виде

(13.5)

При оптимизации последовательное соединение из n инерционных звеньев заменяется одним апериодическим звеном с эквивалентной постоянной времени

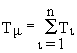так, что

. (13.6)

Основанием для замены последовательно-включенных инерционных звеньев первого порядка одним эквивалентным апериодическим звеном является сходство реакций разомкнутых систем, описываемых передаточными функциями (13.5 ) и (13.6 ) , на скачкообразное входное воздействие. Реакция системы с эквивалентным апериодическим звеном, обладающим постоянной времени T_m представлена кривой 1 на рис. 13.2 ,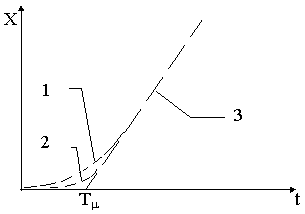

Рис. 13.2.

Кривая 2 иллюстрирует реакцию системы из n последовательно включенных инерционных звеньев с суммой постоянных T_m. Кривая 3 иллюстрирует установившееся движение системы. Она представляет собою линейно возрастающую функцию времени, со скоростью, определяемой параметрами И-регулятора и смещением относительно времени подачи воздействия на величину T_m. С ростом числа n при неизменной суммарной постоянной времени T_m кривая реакции теснее прилегает к оси времени и при n® Ґ совпадает с этой осью, что характерно для системы с чистым запаздыванием (t = T_m ).

Из сказанного можно сделать следующие выводы

- последовательное соединение большого числа инерционных звеньев без большого ущерба для точности можно заменить одним инерционным звеном, постоянная времени которого T_m равна сумме постоянных времени инерционных звеньев. При этом надо, чтобы в контуре имелось хотя бы одно интегрирующее звено или хотя бы одно инерционное звено с постоянной времени во много раз большей, чем сумма малых постоянных времени,

Выбор параметров регулятора осуществляется из условия

Следовательно,

2 T_m =Т_и/К_об®Т_и=2 T_m К_об

Время переходного процесса в оптимизированной контуре составляет величину 6 T_m.

2. Объект содержит ряд апериодических звеньев первого порядка постоянные времени объекта - соизмеримы и t _з№0.

В этом случае оптимизация контура осуществляется также с помощью И-регулятора, причем

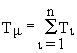+t .

Следует иметь ввиду, что апериодическое звено с эквивалентной постоянной времени T_m, является фиктивным и его инерционность не может скомпенсирована обычным образом с помощью одного ПД- или ПИ- регулятора. Поэтому постоянную времени T_m часто называют некомпенсированной постоянной времени.

3. Если объект с передаточной функцией общего вида содержит одно инерционное звено с большой постоянной времени Т₁, такой что

Т_1і+t .

то при оптимизации следует принять меры для компенсации этой большой постоянной с помощью ПИ-регулятора. Заменив звенья с малыми инерционностями и чистым запаздыванием одним эквивалентным апериодическим звеном с постоянной времени

T_m =+t .

Тогда

Выбирая Т_и=Т₁, получим

Условием оптимальной настройки, кроме Т_и=Т₁ будет

2T_m = Т₁/ К_об К_п®К_п=Т₁/ 2К_обT_m

Таким образом время переходного процесса в контуре, настроенном на “технический оптимум” полностью определяется величиной малой некомпенсированной постоянной времени T_m

t_п=6 T_m

и повышение быстродействия достигается мерами по уменьшению этой постоянной.

в) Если в цепочке инерционных звеньев, из которых состоит объект находятся не одна, а две большие инерционности, т.е.

Т₁> T₂> +t .

то для оптимизации контура следует использовать ПИД-регулятор. Заменив цепочку звеньев с малой инерционностью одним апериодическим звеном первого порядка с постоянной времени

T_m =+t .

запишем передаточную функцию разомкнутой системы в виде

где Т_и и Т_д - соответственно время изодрома и время предварения ПИД-регулятора.

Выбирая Т_и=Т₁и Т_д=Т₂ , получим

Условием оптимальной настройки, кроме Т_и=Т₁ и Т_д=Т₂ будет

2T_m = Т₁/ К_об К_п®К_п=Т₁/ 2К_обT_m

Следует заметить, что большую из двух постоянных необходимо всегда компенсировать временем изодрома, а меньшую - временем предварения. Это связано со спецификой реализации ПИД-регулятора и взаимозависимостью параметров его настроек.

Исключение из передаточной функции разомкнутого контура звеньев с большими и средними постоянными времени открывает возможности повышения быстродействия контура регулирования. Эта операция реальные физические инерционные звенья из контура разумеется не исключает. Однако их действие, замедляющее протекание переходных процессов, компенсируется действием соответствующих форсирующих звеньев, содержащихся в регуляторе, ускоряющих в требуемой степени реакцию системы.

Пытаться компенсировать весьма малые постоянные времени нецелесообразно, так как технические трудности компенсации быстро возрастают при уменьшении значений постоянных времени, а влияние на быстродействие системы соответственно убывает. Особые трудности представляет компенсация дискретности и малого запаздывания ряда быстродействующих электрических преобразователей.

Пример: Статический объект содержит четыре последовательно соединенных апериодических звена с постоянными времени Т₁= 400 мс, Т₂= 80 мс, Т₃= 15 мс, Т₄= 5 мс. Определить расчетное время переходного процесса в контурах, оптимизированных с помощь. И- ПИ- и ПИД- регуляторов.

Тип регулятора	Т_m , мс	t_п, мс
И	500	3000
ПИ	100	600
ПИД	20	120

Настройка на “симметричный оптимум”

Передаточной функции

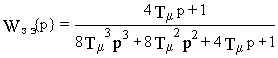
(13.7)

соответствующей контуру, настроенному на симметричный оптимум, описывается система, имеющая в прямом канале звено с передаточной функцией

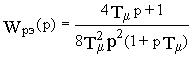
(13.8)

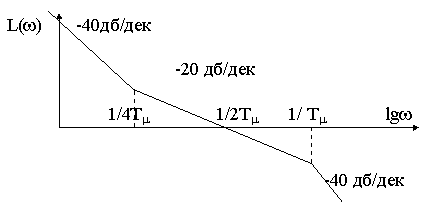
Рис. 13.3.

Как видно, изломы частотной характеристики расположены симметрично относительно частоты среза, откуда и пошло название “симметричный оптимум”.

И в этом случае оптимизация практически состоит в пригонке передаточной функции прямого канала оптимизируемой системы к эталонному виду (13.8) путем выбора подходящего типа регулятора и его настроек. Основные приемы оптимизации - те же, что и в рассмотренных ранее случаях .

а). Если объект содержит одно интегирующее и одно инерционное звено первого порядка, т.е.

то для оптимизации контура используется ПИ-регулятор.

Если время изодрома регулятора выбрать из условия компен-сации постоянной времени объекта (Т_и=Т_об) , то передаточная функция разомкнутого контура примет вид

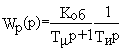
и замкнутая единичной обратной связью система будет находиться на границе устойчивости при любом значении коэффициента передачи К_п (настроечного параметра) . Следовательно, в данном случае компен-сировать постоянную времени объекта нельзя и последнюю следует принять в качестве некомпенсируемой постоянной T_m (T_m =T_об). Для пригонки передаточной функции разомкнутой системы к эталонной (13.8) остается выполнить условия

4T_m =T_ии T_m / К_об К_п = 8T_m ² ® К_п=1/ 8 T_об К_об(13.9)

Нетрудно установить, что время переходного процесса в замкнутом контуре составляет величину t_п=12 T_об .

б) Если объект содержит интегрирующее звено и ряд инерционных звеньев с соизмеримыми постоянными времени Тi , то как и ранее последние следует заменить одним эквивалентным апериодическим звеном с эквивалентной постоянной времени

в) Если объект с передаточной функцией общего вида содержит одно инерционное звено с большой постоянной времени Т₁, такой что

Т_1і

то при оптимизации следует принять меры для компенсации этой большой постоянной с помощью ПИД-регулятора. Заменим звенья с малыми инерционностями и чистым запаздыванием одним эквивалентным апериодическим звеном с постоянной времени

Tm =+t .

Тогда

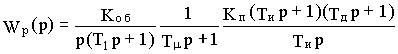
Выбирая Т_д=Т₁, получим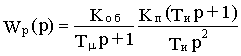

Условием оптимальной настройки, кроме Т_д=Т₁ будут условия

4T_m =T_ии T_m / К_об К_п = 8T_m ² ® К_п=1/ 8 T_m К_об

Таким образом время переходного процесса в контуре, настроенном на “симметричный оптимум” полностью определяется величиной малой некомпенсированной постоянной времени T_m

t_п=12 T_m

и повышение быстродействия достигается мерами по уменьшению этой постоянной.