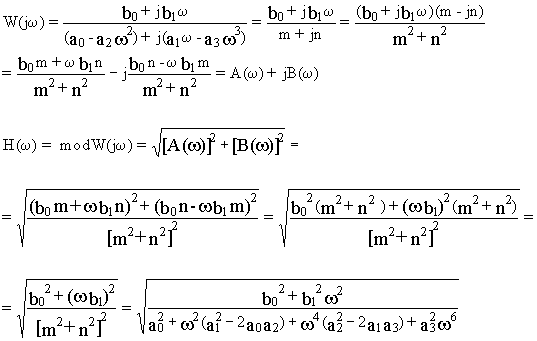
ЛЕКЦИЯ 12
Оптимизация линейных контуров регулирования
Задача оптимизации и типовые настройки контуров
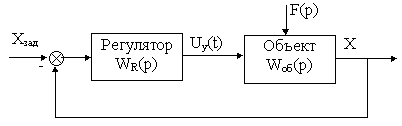
Обобщенная структурная схема линейного контура регулирования представлена на рис. 12.1.

Рис. 12.1.
Если данные и свойства объекта регулирования известны, то задача синтеза состоит в таком выборе регулятора и его параметров, при которых формируемое им управляющее водействие u(t) было бы в состоянии как можно быстро, точно и без возникновения колебаний заставить регулируемую величину X следовать за задающим воздействием Xзад и нейтрализовать возмущения F.
Идеальная система, следовательно, должна удовлетворять следующим двум условиям
W
з у (p)= X(p)/ Xзад(p)=1W
з в (p)= X(p)/F(p)=0Можно сказать, что модуль АФЧХ замкнутой системы в идеальном случае должен быть равен единице во всем диапазоне частот изменения управляющего воздействия (прямая 1 на рис.12.2)
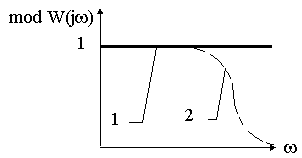
Рис. 12.2.
При наличии инерционности в объекте регулирования указанные условия практически не реализуемы и можно говорить лишь о приближении в максимально возможном диапазоне частот модуля реальной АФЧХ к единице.
В большинстве же случаев ставится задача - ликвидировать влияние инерции объекта настолько полно, насколько это окажется возможным за счет выбора оптимального типа регулятора и его настроек. Такую задачу и называют оптимизацией.
При оптимизации стремятся приблизить АФЧХ замкнутого контура к единице в возможно более широкой полосе частот и при этом обеспечить устойчивость контура и хорошо демпфированный слабоколебательный переходный процесс с минимальным временем. Сама АФЧХ при этом принимает вид кривой “2” на рис. 12.2.
Такая пригонка обеспечивает высокую точность воспроизведения контуром регулирования управляющих и возмущающих воздействий в нижнем диапазоне частот и рост погрешностей с ростом частот этих воздействий. Чем шире диапазон частот, где АФЧХ замкнутой системы близка к единице, тем более высокие частоты может воспроизводить или парировать система.
Основные характеристики контуров,
настроенных на технический оптимум
Если объекты регулирования не содержат в своем составе интегрирующих звеньв, то при оптимизации стремятся получить передаточные функции замкнутых контуров регулирования в виде

![]() (12.1)
(12.1)
Такой прием носит название настройки на “технический оптимум” или “Betragsoptimum” (нем.)
Передаточной функции (12.1) соответствует следующее выражение для модуля АФЧХ H(
w )H(
w ) = mod Wз(jw )=
(Вывод его приведен в приложении 1)
Если потребовать, чтобы H(
w )= 1 при w ® 0 , то для этого следует выполнить условияa0=b0 ; a12= 2 a0a2 ![]()
При этом выражение для АФЧХ оптимизированного контура примет вид
H(
w )= mod Wз(jw )=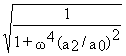
Условие 12.3 являются первым условием оптимизации, причем очень важным. Разумеется, добиться точного равенства единице модуля АФЧХ можно только при нулевой частоте. Однако при весьма низких частотах вполне достижимо хорошее приближение к единице.
Сам замкнутый контур, настроенный на технический оптимум имеет передаточную функцию

или с учетом условий оптимизации (12.3)
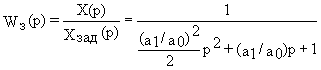
Вводя обозначение (a1/a0)=2T
m , получим передаточную функцию контура, настроенного на технический оптимум в окончательном виде ,
, ![]() (12.4)
(12.4)
Полином знаменателя (характеристическое уравнение) оптимизированного замкнутого контура имеет пару комплексно-сопряженных корней вида
![]() ,
,
где
d = 1/2Tm и W св=1/ 2Tmи следовательно, переходная характеристика оптимизированного контура определяется выражением
![]()
График переходной характеристики оптимизированного контура имеет при этом вид
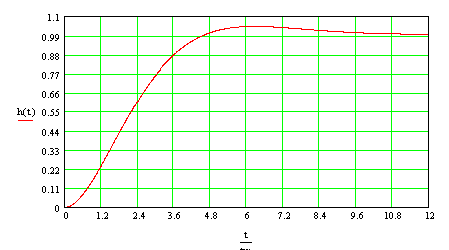
Из рисунка видно, что
-
время первого достижения функцией уровня нового устано-вившегося значения равноt
р1= 4.7 Tm .-время переходного процесса (время вхождения в область значений, отличающихся не более чем на 5% от установившегося значения равно
t
п= 6 Tm .- а перерегулирование
D
Xмакс= 4.3%Эти характеристики типичны для любого контура, настроенного на технический оптимум и при изменении величины малой некомпенсированной постоянной времени T
m меняется лишь масштаб по оси времени.
Основные характеристики контуров, настроенных на симметричный оптимум
Если объекты регулирования имеют в своем составе интегрирующие звенья, то при настройке стремятся привести передаточную функцию оптимизированного контура к виду
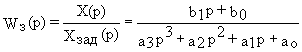
![]() (12.5)
(12.5)
Передаточной функции (7.5) соответствует выражение для АФЧХ следующего вида
H(
w )= mod Wз(jw )=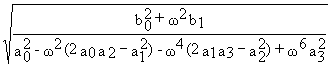
(Вывод его представлен в приложении 2.)
Для пригонки этого выражениея к единице при
w ® 0 необходимо выполнить условия (12.3), т.е.a0=b0 ; a12= 2 a0a2
и кроме того
a1=b1
и a22= 2a1a3
При этом выражение для АФЧХ примет вид
H(
w )= mod Wз(jw )=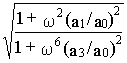
Используя условия оптимизации (12.3) и (12.7) приведем передаточную функцию (12.5) к виду
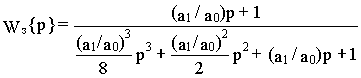
Вводя обозначение (a1/a0)=4T
m, получим передаточную функцию контура, настроенного на симметричный оптимум в окончательном виде
![]() (12.9)
(12.9)
Среди полюсов передаточной функции (корней полинома знаменателя) имеется один вещественный корень
p1= - 1/2 T
mи пара комплексно-сопряженных корней
p2,3= -1/4 T
m ± j(Ц 3/4 Tm )(Примеч: При нахождении корней целесообразно использовать разложение
1+8 T
m 3 p3= 1+(2 pTm )3= (1+2pTm )(1-2pTm +4Tm 2 p2)Находя переходную характеристику контура как
h(t)=L-1{W(p)/p},
получим
h(t)= 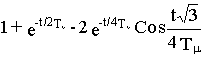
Последнему выражению соответствует следующий график

Рис. 12.4
.Из графика видно, что
- время первого согласования для симметрично оптимизированного контура
t
р1= 3.1 Tm .-время переходного процесса (время вхождения в область значений, отличающихся не более чем на 5% от установившегося значения равно
t
п= 12Tm .- а перерегулирование
D
Xмакс= 43%
Приложение1.
Производя подстановку p=j
w в выражение (12.1), получим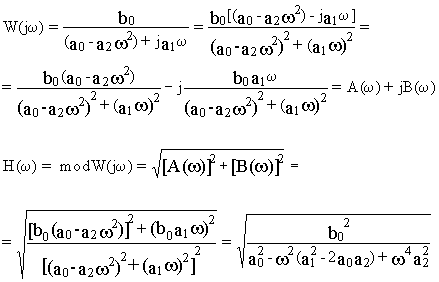
Приложение 2.
Производя подстановку p=j
w в выражение (12.5), получим