НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ. При изучении индуктивно-связанных цепей нами был рассмотрен воздушный трансформатор, отличающийся малым значением коэффициента связи между обмотками
НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ. При изучении индуктивно-связанных цепей нами был рассмотрен воздушный трансформатор, отличающийся малым значением коэффициента связи между обмоткамиЛекция 2
Трансформатор с ферромагнитным сердечником
 НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ. При изучении индуктивно-связанных цепей нами был рассмотрен воздушный трансформатор, отличающийся малым значением коэффициента связи между обмотками
НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ. При изучении индуктивно-связанных цепей нами был рассмотрен воздушный трансформатор, отличающийся малым значением коэффициента связи между обмотками
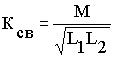
в силу того, что доля потоков рассеяния Ф
s в общих потоках, создаваемых токами первичной и вторичной обмоток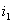 и
и 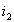 была велика по сравнению с потоками взаимоиндукции. Значение взаимной индуктивности
была велика по сравнению с потоками взаимоиндукции. Значение взаимной индуктивности
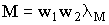
было мало, в силу малого значения магнитной проводимости воздуха, по которому замыкался рабочий поток трансформатора (или поток взаимной индукции).
Для улучшении магнитной связи между первичной и вторичной обмотками трансформатора последние размещают на сердечнике из ферромагнитного материала, как схематично показано на рис.2.1.
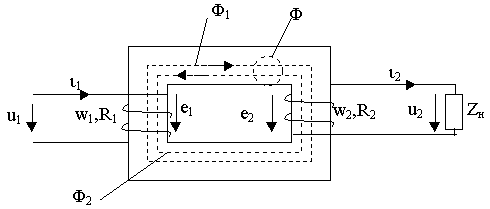
Рис. 2.1
Как и ранее к первичной обмотке с числом витков 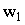 подводится синусоидальное напряжение u
подводится синусоидальное напряжение u
 сети, от другой обмотки (вторичной) с числом витков w2 энергия отводится к нагрузке. Периодические переменные токи обмоток
сети, от другой обмотки (вторичной) с числом витков w2 энергия отводится к нагрузке. Периодические переменные токи обмоток 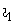 и
и 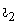 создают в сердечнике магнитное поле, изменение которого сопровождается циклическим перемагничиванием материала сердечника. Особенности такого трансформатора обуславливаются высокой магнитной проницаемостью материала сердечника, нелинейной зависимостью между напряженностью магнитного поля и индукцией в сердечнике и потерями энергии на перемагничивание сердечника.
создают в сердечнике магнитное поле, изменение которого сопровождается циклическим перемагничиванием материала сердечника. Особенности такого трансформатора обуславливаются высокой магнитной проницаемостью материала сердечника, нелинейной зависимостью между напряженностью магнитного поля и индукцией в сердечнике и потерями энергии на перемагничивание сердечника.
РАБОТА ТРАНСФОРМАТОРА В РЕЖИМЕ ХОЛОСТОГО ХОДА. Под холостым ходом понимается режим работы трансформатора при разомкнутой вторичной обмотке, когда ток 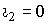 (схема рис.2-2).
(схема рис.2-2).
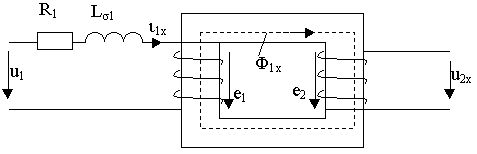
Рис. 2.2
В этом случае в первичной цепи трансформатора протекает ток холостого хода 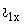 и уравнение электрического состояния трансформатора относительно мгновенных значений токов и напряжений имеют вид
и уравнение электрического состояния трансформатора относительно мгновенных значений токов и напряжений имеют вид
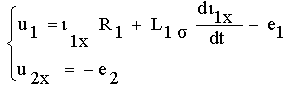
где 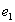 и
и 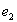 –ЭДС, наводимые в первичной и вторичной обмотках потоком
–ЭДС, наводимые в первичной и вторичной обмотках потоком 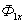 , замыкающимся по сердечнику, причем
, замыкающимся по сердечнику, причем
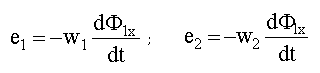
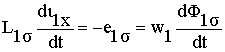 - напряжение, уравнивающее ЭДС рассеяния первичной обмотки.
- напряжение, уравнивающее ЭДС рассеяния первичной обмотки.
Поскольку m 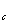
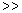 m
m 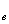 и, следовательно
и, следовательно 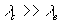 , то
, то 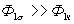 и
и 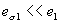 .
.
Ток, который течет в первичной обмотке 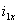 , как и ток рассмотренной выше катушки с ферромагнитным сердечником, несинусоидален при синусоидальном напряжении на первичной обмотке и, следовательно, при синусоидальном потоке
, как и ток рассмотренной выше катушки с ферромагнитным сердечником, несинусоидален при синусоидальном напряжении на первичной обмотке и, следовательно, при синусоидальном потоке 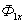 и может быть заменен эквивалентным синусоидальным током, содержащим активную и реактивную составляющие, т.е.
и может быть заменен эквивалентным синусоидальным током, содержащим активную и реактивную составляющие, т.е.
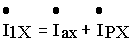 .
.
При этом уравнения электрического состояния трансформатора относительно эквивалентных синусоид можно записать в комплексной форме
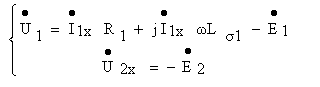
При работе трансформатора в режиме холостого хода энергия, подводимая к трансформатору от сети расходуется на перемагничивание сердечника и на нагрев первичной обмотки, т.е.
PX=PM1+Pcm
Однако потери в меди силовых трансформаторов в режиме холостого хода 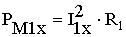
малы, в силу того, что мал ток холостого хода правильно спроектированного трансформатора. Обычно 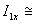
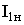 , где
, где 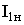 - номинальный ток первичной обмотки (или ток в первичной обмотке при номинальной нагрузке трансформатора). Поэтому приближенно считают, что при ХХ имеют место лишь потери в стали, т.е.
- номинальный ток первичной обмотки (или ток в первичной обмотке при номинальной нагрузке трансформатора). Поэтому приближенно считают, что при ХХ имеют место лишь потери в стали, т.е. 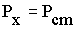 .
.
Примечание: Здесь следует заметить, что поток 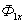 и ЭДС
и ЭДС 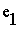 , наводимые в витках идеализированных катушек (с ферромагнитным сердечником и без него) одинаковы при одинаковом числе витков
, наводимые в витках идеализированных катушек (с ферромагнитным сердечником и без него) одинаковы при одинаковом числе витков 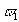 и однозначно определяются приложенным напряжением, т. е.
и однозначно определяются приложенным напряжением, т. е.
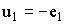
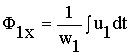 ,
,
как было показано выше. Намагничивающие же силы и, следовательно, намагничивающие токи, требуемые для создания этих потоков, различны и тем меньше, чем меньше магнитное сопротивление пути, по которому замыкается магнитный поток. По закону Ома для магнитных цепей 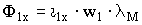 и, следовательно
и, следовательно 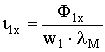 . Таким образом, ток холостого хода трансформатора с ферромагнитным сердечником (магнитная проницаемость которого
. Таким образом, ток холостого хода трансформатора с ферромагнитным сердечником (магнитная проницаемость которого
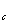
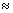 1000 и выше) во много раз меньше тока холостого хода воздушного трансформатора (m
1000 и выше) во много раз меньше тока холостого хода воздушного трансформатора (m 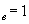 ) при одинаковом напряжении
) при одинаковом напряжении 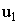 и числе витков
и числе витков 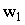 .
.
Векторная диаграмма трансформатора в режиме ХХ, приведенная на рис. 2.3, практически не отличается от векторной диаграммы катушки с ферромагнитным сердечником, рассмотренной ранее.
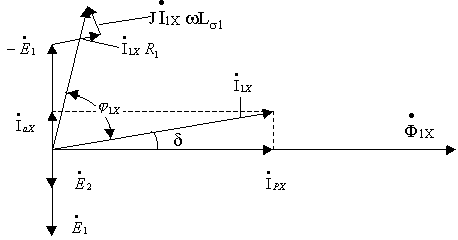
Рис. 2.3
В этом режиме ток 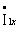 отстает от напряжения
отстает от напряжения 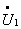 на угол
на угол
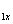 =(84-85)° , т.к. угол потерь d @ 5-6° . Cos j
=(84-85)° , т.к. угол потерь d @ 5-6° . Cos j 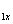 = (0.2-0.3)
= (0.2-0.3)
Обычно при выполнении магнитопровода из электротехнической стали толщиной 0,35-0,5 мм и частоте сети f=50Гц I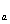
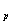 . Поэтому активная составляющая тока ХХ оказывает малое влияние на форму тока ХХ. Эта форма определяется в основном реактивной составляющей тока холостого хода.
. Поэтому активная составляющая тока ХХ оказывает малое влияние на форму тока ХХ. Эта форма определяется в основном реактивной составляющей тока холостого хода.
РАБОТА ТРАНСФОРМАТОРА ПОД НАГРУЗКОЙ. При подключении сопротивления нагрузки 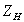 к зажимам вторичной обмотки в ней появляется ток
к зажимам вторичной обмотки в ней появляется ток 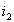 и уравнения электрического состояния трансформатора можно записать в виде
и уравнения электрического состояния трансформатора можно записать в виде
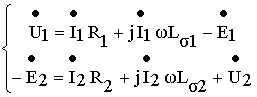
Эти уравнения, записанные в комплексной форме относительно эквивалентных синусоид, ничем не отличаются от соответствующих уравнений воздушного трансформатора.
Анализируя работу трансформатора под нагрузкой, важно уяснить взаимосвязь тока в цепи нагрузки 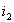 с током, потребляемым трансформатором от сети, поскольку изменение мощности, отдаваемой трансформатором в нагрузку должно сопровождаться изменением мощности, потребляемой трансформатором от сети. Эта взаимосвязь устанавливается через уравнение магнитного состояния трансформатора.
с током, потребляемым трансформатором от сети, поскольку изменение мощности, отдаваемой трансформатором в нагрузку должно сопровождаться изменением мощности, потребляемой трансформатором от сети. Эта взаимосвязь устанавливается через уравнение магнитного состояния трансформатора.
При изучении воздушного трансформатора нами было установлено, что 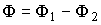 , т.е. основной или рабочий поток трансформатора равен алгебраической сумме потоков взаимоиндукции первичной и вторичной обмоток
, т.е. основной или рабочий поток трансформатора равен алгебраической сумме потоков взаимоиндукции первичной и вторичной обмоток 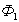 и
и 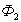 или
или
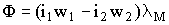 ,
,
где 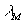 - магнитная проводимость участка, по которому замыкаются потоки взаимоиндукции.
- магнитная проводимость участка, по которому замыкаются потоки взаимоиндукции.
(В соответствие с принципом Ленца поток 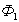 направлен встречно потоку
направлен встречно потоку 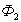
Следовательно, в режиме ХХ 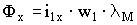
а под нагрузкой 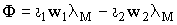
Если пренебречь напряжениями 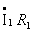 и
и 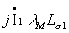 по сравнению с ЭДС
по сравнению с ЭДС 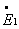 , т.е. считать, что
, т.е. считать, что 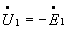 и
и 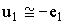 , то поток в сердечнике будет однозначно определяться приложенным напряжением, как было показано выше. Следовательно, поток в сердечнике при одинаковом напряжении будет одинаковым как в режиме ХХ, так и под нагрузкой, т.е.
, то поток в сердечнике будет однозначно определяться приложенным напряжением, как было показано выше. Следовательно, поток в сердечнике при одинаковом напряжении будет одинаковым как в режиме ХХ, так и под нагрузкой, т.е.
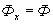 или
или 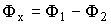 .
.
Физически взаимосвязь токов 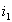 и
и 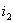 объясняется следующим образом: в режиме ХХ ток холостого хода
объясняется следующим образом: в режиме ХХ ток холостого хода 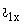 создает поток в сердечнике
создает поток в сердечнике 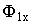 , обуславливающий ЭДС
, обуславливающий ЭДС
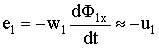
Ток 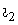 , протекающий через нагрузку, создает поток
, протекающий через нагрузку, создает поток 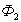 , стремящийся ослабить поток Ф. Но уменьшение потока Ф приводит к уменьшению ЭДС
, стремящийся ослабить поток Ф. Но уменьшение потока Ф приводит к уменьшению ЭДС 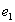 , и, следовательно, к нарушению равенства
, и, следовательно, к нарушению равенства 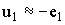 . Следовательно, ток
. Следовательно, ток 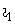 начинает возрастать и будет расти до тех пор, пока поток не достигнет прежнего значения
начинает возрастать и будет расти до тех пор, пока поток не достигнет прежнего значения 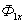
Из равенства 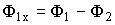 или
или 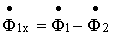 , поскольку потоки синусоидальны, следует, что
, поскольку потоки синусоидальны, следует, что
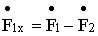
Последнее уравнение представляет собой закон равновесия намагничивающих сил трансформатора или уравнения магнитного состояния трансформатора. Поскольку 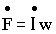 , последнее уравнение можно записать в виде
, последнее уравнение можно записать в виде
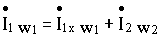
или
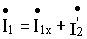 ,
,
где 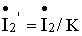 - приведенный ток вторичной обмотки.
- приведенный ток вторичной обмотки.
Согласно последнему уравнению, ток, потребляемый трансформатором от сети 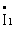 имеет 2 составляющие: составляющая
имеет 2 составляющие: составляющая 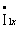 создает рабочий поток в сердечнике и компенсирует потери в стали, составляющая
создает рабочий поток в сердечнике и компенсирует потери в стали, составляющая 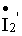 (нагрузочная составляющая) компенсирует размагничивающее действие на сердечник тока вторичной обмотки и обеспечивает поступление в трансформатор от сети мощности, отдаваемой в нагрузку.
(нагрузочная составляющая) компенсирует размагничивающее действие на сердечник тока вторичной обмотки и обеспечивает поступление в трансформатор от сети мощности, отдаваемой в нагрузку.
Векторная диаграмма трансформатора, работающего на нагрузку приведена, на рис. 2.4.
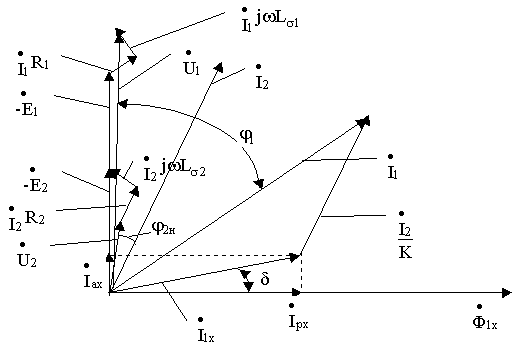
Рис. 2.4
Порядок построения диаграммы :
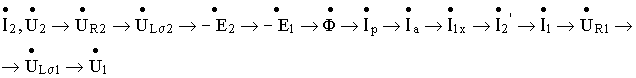
СХЕМА ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРА. В силу того, что уравнения электрического состояния трансформатора с ферромагнитным сердечником для эквивалентных синусоид аналогичны уравнениям воздушного трансформатора, то и схемы замещения этих трансформаторов во многом аналогичны. Особенность схемы замещения трансформатора с ферромагнитным сердечником состоит в наличии ветви с активной проводимостью 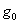 , учитывающей потери в стали реального трансформатора (схема рис. 2.5).
, учитывающей потери в стали реального трансформатора (схема рис. 2.5).
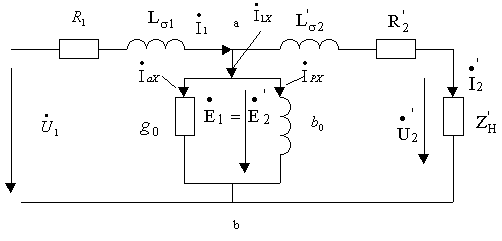
Рис. 2.5
Участок схемы замещения между точками “а” и “б”, аналогичный схеме замещения идеализированной катушки с ферромагнитным сердечником может быть заменен последовательной цепью из сопротивления 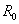 и
и 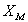 (рис. 2.6) , называемой ветвью холостого хода. Через него проходит ток холостого хода
(рис. 2.6) , называемой ветвью холостого хода. Через него проходит ток холостого хода 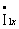
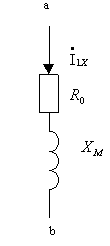
Рис.
2.6Параметры элементов схемы можно определить экспериментально на основании опытов холостого хода и короткого замыкания.
Опыт ХХ проводиться для определения коэффициента трансформации К, потерь в стали и параметров ветви ХХ 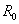 и
и 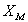 . Опыт ХХ проводится по схеме, приведенной на рис. 2.7 при номинальном напряжении на первичной обмотке
. Опыт ХХ проводится по схеме, приведенной на рис. 2.7 при номинальном напряжении на первичной обмотке 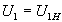 , установленном с помощью ругулятора напряжения РН.
, установленном с помощью ругулятора напряжения РН.
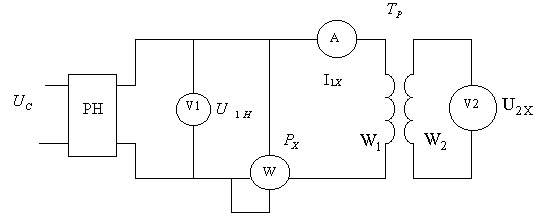
Рис. 2.7
При этом измеряется напряжение на вторичной обмотке 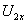 , ток первичной обмотки
, ток первичной обмотки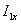 и мощность (активная), потребляемая первичной цепью трансформатора
и мощность (активная), потребляемая первичной цепью трансформатора 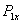
Как уже ранее отмечалось, в режиме ХХ 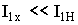
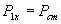 ,
, 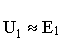 .
.
По данным опыта определяют
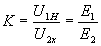 -коэффициент трансформации,
-коэффициент трансформации,
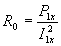 - активное сопротивление ветви ХХ,
- активное сопротивление ветви ХХ,
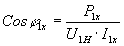 - фазовый сдвиг между напряжением и током в режиме ХХ,
- фазовый сдвиг между напряжением и током в режиме ХХ,
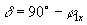 -угол потерь,
-угол потерь,
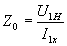 - полное сопротивление ветви ХХ,
- полное сопротивление ветви ХХ,
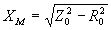 - реактивное сопротивление ветви ХХ.
- реактивное сопротивление ветви ХХ.
Опыт короткого замыкания проводиться для определения активных сопротивлений 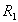 и
и 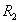 и индуктивностей рассеяния
и индуктивностей рассеяния 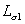 и
и 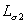 первичной и вторичной обмоток трансформатора. Опыт проводиться по схеме, приведенной на рис. 2-8 при закороченной вторичной обмотке.
первичной и вторичной обмоток трансформатора. Опыт проводиться по схеме, приведенной на рис. 2-8 при закороченной вторичной обмотке.
Рис. 2.8
С помощью регулятора напряжения РН напряжение на первичной обмотке трансформатора постепенно увеличивается до значения, 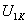 , при котором ток в первичной обмотке достигнет номинального тока
, при котором ток в первичной обмотке достигнет номинального тока 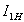 . Это напряжение носит название напряжения короткого замыкания трансформатора. При этом измеряется мощность, потребляемая трансформатором
. Это напряжение носит название напряжения короткого замыкания трансформатора. При этом измеряется мощность, потребляемая трансформатором 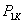
Обычно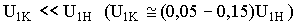 , поэтому поток в сердечнике, определяемый напряжением мал. Следовательно, в режиме КЗ можно пренебречь потерями в стали трансформатора, исключить ветвь ХХ из схемы замещения и представить эту схему в виде рис. 2.9, где
, поэтому поток в сердечнике, определяемый напряжением мал. Следовательно, в режиме КЗ можно пренебречь потерями в стали трансформатора, исключить ветвь ХХ из схемы замещения и представить эту схему в виде рис. 2.9, где
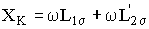 ,
, 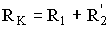 .
.
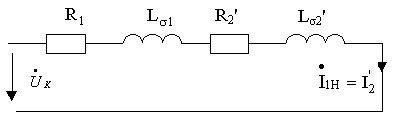
Рис. 2.9
На основании данных измерений определяют
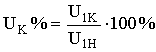 - процентное напряжение КЗ,
- процентное напряжение КЗ,
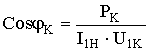 - фазовый сдвиг между напряжением и током в режиме КЗ,
- фазовый сдвиг между напряжением и током в режиме КЗ,
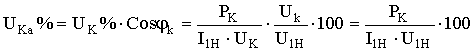 - активная составляющая напряжения КЗ
- активная составляющая напряжения КЗ
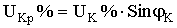 - реактивная составляющая напряжения КЗ.
- реактивная составляющая напряжения КЗ.
Поскольку поток в сердечнике трансформатора и потери в стали в режиме КЗ малы, считается, что вся мощность 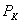 расходуется в меди первичной и вторичной обмоток. Тогда
расходуется в меди первичной и вторичной обмоток. Тогда
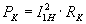
и, следовательно,
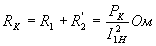 .
.
Так как 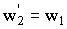 , то
, то 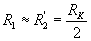 и
и 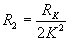
Полное сопротивление короткого замыкания
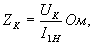
реактивное сопротивление КЗ
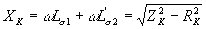
Поскольку 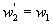 , то
, то 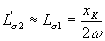 и
и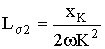
В паспорте или каталожных данных на трансформатор часто указывается величины Uк
%, Uка% и Uкр% . Зная их, можно рассчитать параметры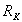 и
и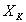 схемы замещения следующим образом:
схемы замещения следующим образом:
Т.к. 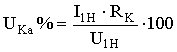 , то
, то 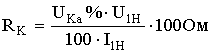 .
.
Т.к. 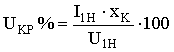 , то
, то 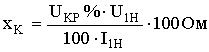
ВНЕШНЯЯ ХАРАКТЕРИСТИКА ТРАНСФОРМАТОРА. При изменении нагрузки трансформатора, его вторичное напряжение 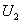 не остается неизменным, как это следует из уравнения Кирхгоффа для вторичной цепи
не остается неизменным, как это следует из уравнения Кирхгоффа для вторичной цепи
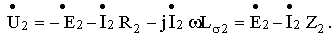
С ростом тока 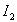 увеличивается падение напряжения на сопротивлении
увеличивается падение напряжения на сопротивлении 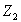 . Зависимость напряжения на вторичной обмотке трансформатора
. Зависимость напряжения на вторичной обмотке трансформатора 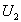 от тока нагрузки
от тока нагрузки 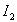 при постоянном напряжении на первичной обмотке
при постоянном напряжении на первичной обмотке 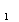 называется внешней характеристикой трансформатора. Изменение вторичного напряжения при переходе от режима ХХ к режиму работы под нагрузкой, выраженное в процентах, определяется выражением
называется внешней характеристикой трансформатора. Изменение вторичного напряжения при переходе от режима ХХ к режиму работы под нагрузкой, выраженное в процентах, определяется выражением
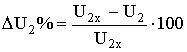
Величина 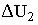 зависит как от величины нагрузки, так и от ее характера, определяемого величиной и знаком угла
зависит как от величины нагрузки, так и от ее характера, определяемого величиной и знаком угла 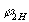 (фазового сдвига между напряжением и током в нагрузке).
(фазового сдвига между напряжением и током в нагрузке). 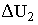 определяется по формуле
определяется по формуле

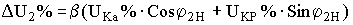
где 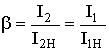 - коэффициент нагрузки трансформатора,
- коэффициент нагрузки трансформатора,
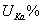 и
и 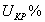 соответственно активная и реактивная составляющие напряжения короткого замыкания
соответственно активная и реактивная составляющие напряжения короткого замыкания 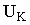 .
.
На рис. 2.10 приведены внешние характеристики трансформатора для различных по характеру нагрузок. При чисто активной нагрузке (Cos
j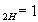 ) и активно- индуктивной нагрузке (Cosj
) и активно- индуктивной нагрузке (Cosj 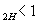 , j
, j 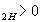 ) внешние характеристики имеют падающий характер.
) внешние характеристики имеют падающий характер.
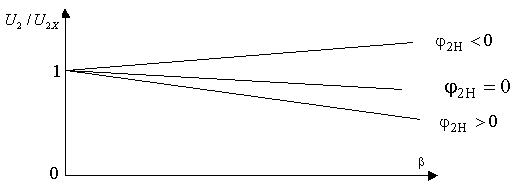
Рис. 2.10
При активно-емкостной нагрузке (Cos
j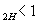 , j
, j 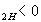 ), рост тока нагрузки может сопровождаться увеличением напряжения на выходе: в силу того, что члены с Sinj
), рост тока нагрузки может сопровождаться увеличением напряжения на выходе: в силу того, что члены с Sinj 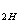 в формуле (*) приобретают знак ( - ).
в формуле (*) приобретают знак ( - ).
Коэффициент полезного действия трансформатора.
Преобразование электрической энергии в трансформаторе сопровождается потерями энергии на нагрев сердечника и обмоток. Уравнение баланса мощностей трансформатора имеет вид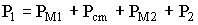
где 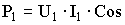
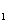 - активная мощность, потребляемая от сети,
- активная мощность, потребляемая от сети,
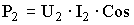 j
j 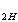 - мощность, отдаваемая в нагрузку,
- мощность, отдаваемая в нагрузку,
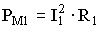 - потери в меди первичной обмотки,
- потери в меди первичной обмотки,
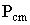 - потери в стали трансформатора,
- потери в стали трансформатора,
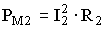 - потери в меди вторичной обмотки.
- потери в меди вторичной обмотки.
Процесс преобразования энергии в трансформаторе иллюстрирует энергетическая диаграмма, приведенная на рис. 2.11.
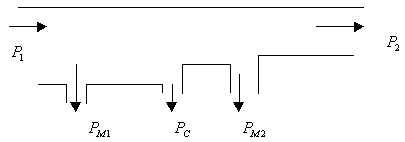
Рис. 2.11
Величина
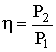
носит названия коэффициента полезного действия трансформатора.
Если обозначить сумму
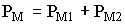
и назвать ее потерями в меди трансформатора, то КПД трансформатора можно выразить так
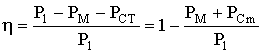
Потери в стали 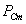 определяются величиной и частотой изменения магнитного потока в сердечнике трансформатора, а так как поток почти не зависит от нагрузки, то потери в стали остаются почти постоянными и равными потерям в режиме ХХ
определяются величиной и частотой изменения магнитного потока в сердечнике трансформатора, а так как поток почти не зависит от нагрузки, то потери в стали остаются почти постоянными и равными потерям в режиме ХХ 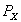
Поскольку потери в меди обмотки пропорциональны квадрату действующего значения тока, через нее протекающего, последние могут быть определены из упрощенной схемы замещения трансформатора (рис 2-) в режиме КЗ.
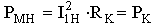 - потери в меди при номинальном токе первичной обмотки,
- потери в меди при номинальном токе первичной обмотки,
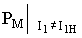 - потери в меди при токе, отличном от номинального,
- потери в меди при токе, отличном от номинального,
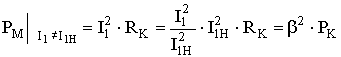 .
.
Активную мощность в нагрузке трансформатора можно вычислить по формуле
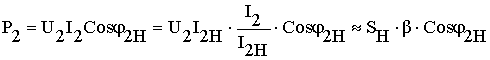 ,
,
где 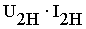
Теперь выражение, определяющее КПД трансформатора можно записать в виде
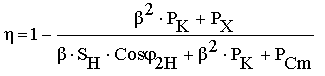
Эта формула рекомендована ГОСТом для определения КПД трансформатора.
Анализ полученного выражения показывает, что КПД неоднозначно зависит от коэффициента нагрузки
b и является функцией характера нагрузки (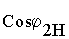 ), что иллюстрируется кривыми, приведенными на рис. 2-12.
), что иллюстрируется кривыми, приведенными на рис. 2-12.
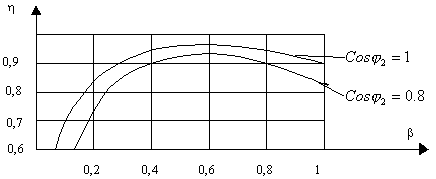
Рис.2.12
При
b =0, h =0. С ростом отдаваемой мощности h увеличивается, т.к. в энергетическом балансе уменьшается удельное значение потерь в стали, имеющих приблизительно постоянное значение. При некотором значении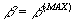 КПД достигает максимума, после чего начинает уменьшаться с ростом тока нагрузки. Причиной этого является увеличение потерь в меди, возрастающих пропорционально квадрату тока (или
КПД достигает максимума, после чего начинает уменьшаться с ростом тока нагрузки. Причиной этого является увеличение потерь в меди, возрастающих пропорционально квадрату тока (или 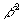 ), в то время как полезная мощность растет пропорционально b. Значение
), в то время как полезная мощность растет пропорционально b. Значение 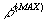 можно получить из условия
можно получить из условия
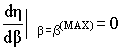 ,
,
при этом
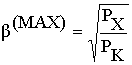 или
или 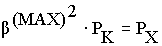
Следовательно КПД имеет максимум при такой нагрузке, при которой потери в меди трансформатора равны потерям в стали. Для трансформаторов большей мощности 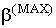 =0,5 - 0,7, при этом
=0,5 - 0,7, при этом 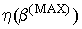 =0,995. Трансформаторы малой мощности рассчитывается как, чтобы
=0,995. Трансформаторы малой мощности рассчитывается как, чтобы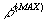 =1, тогда
=1, тогда 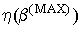 =0,7 – 0,9. При уменьшении величины
=0,7 – 0,9. При уменьшении величины 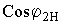 КПД уменьшается, т.к. возрастают токи
КПД уменьшается, т.к. возрастают токи 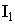 и
и 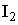 , при которых трансформатор имеет заданную мощность
, при которых трансформатор имеет заданную мощность