Лекция 9

Электрические цепи трехфазного синусоидального тока

Трехфазной системой называется совокупность трехфазного источника и трехфазного приемника, электрически связанных между собой. Трехфазная система по сравнению с однофазной намного сложней, однако, она имеет и ряд преимуществ.

  1. Экономичность производства и передачи энергии по сравнению с однофазной

  2. Возможность сравнительно простого получения вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя- одного из самых распространенных двигателей переменного тока

  3. Возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.

Элементы трехфазной системы

Трехфазные источники

Трехфазным источником называется совокупность трех однофазных источников одинаковой частоты с суммарным фазовым сдвигом равным 2p .

Если амплитуды ЭДС в каждой фазе одинаковые и сдвиг по фазе между двумя любыми смежными ЭДС равен 2p /3, то система ЭДС называется симметричной. При несоблюдении любого из этих условий система ЭДС называется несимметричной.

Выражения для мгновенных значений ЭДС симметричной трехфазной системы можно представить в следующем виде:

eA = Em sinωt , eB = Em sin(ωt - 2p /3), eC = Em sin(ωt - 4p /3).

При переходе к комплексным амплитудам имеем

mA = Em , mB = Em e- j2p /3 , mC = Em e- j4p /3 = Em e+ j2p /3.

Важным свойством симметричной трехфазной системы является равенство нулю суммы мгновенных значений фазных ЭДС , т.е.

eA + eB + eC = 0.

Справедливым является и равенство

mA + mB + mC = Em (1 + e- j2p /3 + e+ j2p /3 ) = 0,

что легко показать и на векторной диаграмме.

Чтобы уменьшить число проводов, которыми соединяются трехфазные источники и трехфазные приемники, и тем самым сократить стоимость линии электропередачи, отдельные фазы источников соединяют между собой по схеме “звезда” или “ треугольник”.

Соединение источников по схеме “звезда”

При соединении звездой концы X,Y,Z трех фаз (рис.9.1, а ), соединяют в один общий узел. Этот общий узел “О”называется нейтралью или нулевой точкой. За положительные направления ЭДС источников еА, еB, еC принимают направления от концов фаз к их началам (A,B,C). Для характеристики трехфазного источника используют понятия фазных и линейных напряжений.

Фазными напряжениями источника называют напряжения A, B, C между началами и концами фаз источника ( генератора или трансформатора) .

Провода, соединяющие зажимы А,В,С источника с приемниками, называются линейными. Токи А,B,C, протекаюшие в линейных проводах, называются линейными. Напряжения между линейными проводами называются линейными. На рис. 9.1,а эти напряжения обозначены как AB ,BC, ,CA.. Видно, что

AB = A - B , BC = B - C , CA = C - A .

Векторная диаграмма, соответствующая полученным уравнениям, представлена на рис. 9.1,б. Анализ этой диаграммы показывает, что

а) если равны действующие значения фазных напряжений источника, т.е.

UA =UB =UC = UФ ,

то равны и действующие значения линейных напряжений источника, т.е.

UAB =UBC =UCA = Uл;

б) из геометрических соотношений легко установить, что Uл =Ц 3Uф;

в) если фазные напряжения образуют симметричную трехфазную систему, то и линейные напряжения образуют симметричную трехфазную систему, т.е.

AB + BC + CA=0.

Наиболее распространены номинальные напряжения промышленных электрических сетей 380 В, 220 В, 127 В. При соединении звездой при Uл=380 В Uф=380/Ц 3=220 В, при Uл=220 В Uф=220/Ц 3=127 В.

Это дает возможность включать однофазные приемники, рассчитанные на 2 напряжения к одному трехфазному источнику.

 

 

Соединение фаз источника треугольником

При соединении фаз источника треугольником конец X фазы АX соединяется с началом B фазы BY, конец Y фазы BY соединяется с началом C фазы CZ и конец Z последней – с началом A фазы АX. Такая схема представлена на рис. 9.2,а, а векторная диаграмма – на рис. 9.2,б.

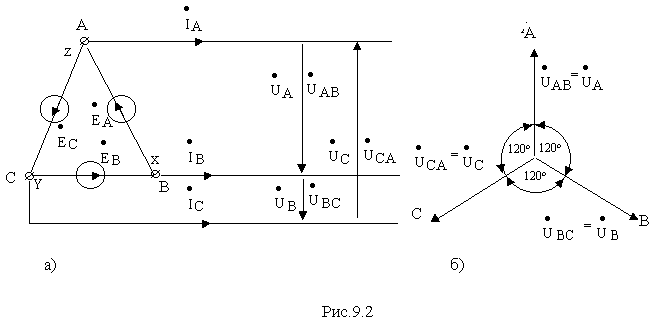
Анализируя схему и векторную диаграмму легко установить, что

а) линейные напряжения источника равны соответствующим фазным напряже-ниям, т.е. AВ = A , BC=B,, CA=C ;

б) для симметричной трехфазной системы ЭДС действующие значения линейных и фазных напряжений одинаковы, т.е

UA =UB =UC =UAB =UBC =UCA= Uл =Uф.

в) в замкнутом контуре, образованном источниками, не возникает тока только при идеальной симметриии источников, когда выполняется равенство eA + eB + eC = 0. При наличии несимметрии ток в этом контуре возникает даже при отсутствии нагрузки.

Трехфазные приемники (нагрузки)

Трехфазные приемники, как и источники, могут быть соединены звездой или треугольником, как показано на рис.9.3,а,б.

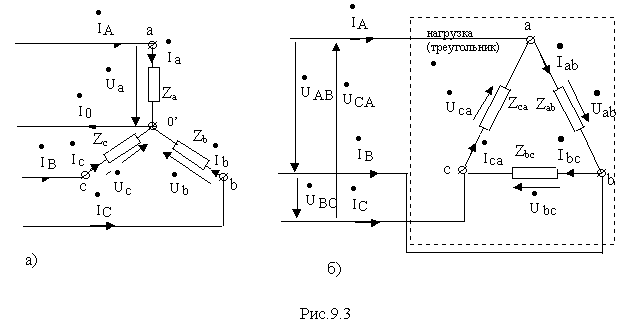
Если комплексные сопротивления фаз равны между собой, то нагрузка фаз называется симметричной. Если комплексные сопротивления фаз отличны друг от друга, то нагрузка называется несимметричной. Если пренебречь сопротивлениями линейных проводов, то в обоих случаях линейные напряжения трехфазных приемников равны соотвествующим линейным напряжениям источников, т.е.

AВ = ab , BC=bc,, CA=ca

Для нагрузки, фазы которой Za, Zb и Zc соединены звездой (рис.9.3,а), токи в фазах всегда равны соответствующим линейным токам, т.е. A=a, B=b, C=c. Напряжения на фазах нагрузки зависят от способа соединения с источником ( трехпроводной или четырехпроводной) и от параметров нагрузки.

При соединении треугольником ( рис.9.3,б) нагрузка каждой фазы включается непосредственно между линейными проводами и поэтому всегда фазные напряжения на нагрузке равны соответствующим линейным напряжениям источника. Токи в фазах нагрузки находятся по закону Ома как

ab = YabAB ,bc = YbcBC ,ca = YcaCA ,

где Yab, Yсb, Yсa –комплексные проводимости фаз.

Применяя первый закон Кирхгофа к узлам цепи, получим линейные токи, выраженные через фазные токи:

A = ab - ca ,B = bc - ab ,C = ca - bc

Векторная диаграмма, соответствующая общему несимметричной нагрузки приведена на рис.9.4,а . Диаграмма на рис. 9.4,б соответствует симметричной нагрузке.

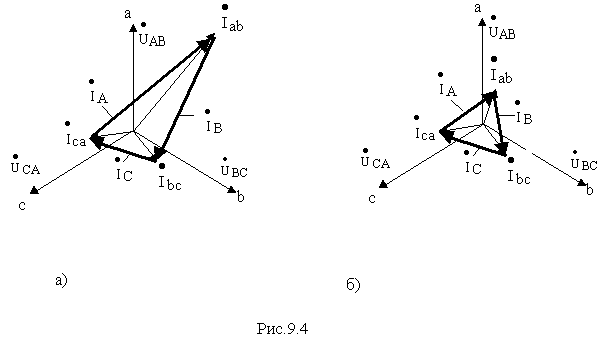
Для симметричной нагрузки справедливы равенства

Iab=Ibc=Ica=Iф

и

Iл = I IФ.

Важной особенностью соединения приемников треугольником является независимость режима работы каждой фазы от других фаз. При изменении сопротивления в одной из фаз будут меняться ток данной фазы и линейные токи в проводах, соединенных с этой фазой. Токи в двух других фазах при этом не изменятся. Поэтому схема соединения приемников треугольником широко используется при несимметричной нагрузке фаз.

Расчет и анализ различных схем трехфазных цепей

Четырехпроводная схема “звезда-звезда” (рис. 9.5,а).

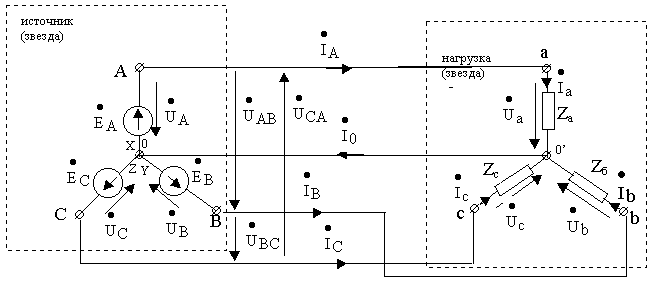
Здесь источник и нагрузку связывают не только три линейных провода, но и провод, соединяющий нулевые точки источника и приемника (нулевой провод). Ток в этом проводе называется нулевым и обозначается 0.

В этой схеме фазные напряжения источника и приемника одинаковы, т.е.

A=a, B=b, C=c.

Линейные токи находятся на основании закона Ома как

A = YaA ,B = YbB , C = YcC .

Ток в нулевом проводе находится на основании узлового уравнения Кирхгофа как сумма линейных токов

0=A+ B+ C.

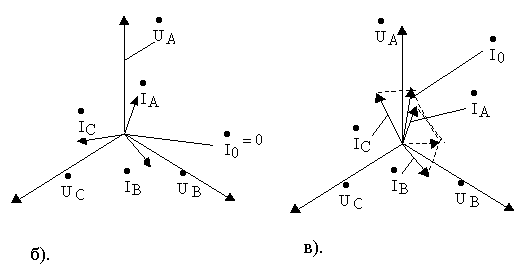
При симметричной нагрузке токи в фазах образуют симметричную систему токов и потому ток в нулевом проводе равен 0, т.е. 0=A+ B+ C=0. Этому случаю соответствует векторная диаграмма, представленная на рис. 9.5,б.

Рис. 9.5

При несимметричной нагрузке ток в нулевом проводе не равен 0, т.е. 0=A+ B+C№ 0. Этому случаю соответствует векторная диаграмма, представленная на рис. 9.5,в. В этом случае изменение сопротивления одной из фаз нагрузки влияет на ток только данной фазы и ток в нулевом проводе.

Трехпроводная схема “звезда-звезда” (рис. 9.6,а).

Рис. 9.6

В общем случае в этой схеме из-за отсутствия нулевого провода фазные напряжения приемника не равны фазным напряжениям источника и могут быть найдены на основании второго закона Кирхгофа по формулам

a = A - 0 , b = B - 0 , c = C - 0 ,

где 0 –напряжение смещения нейтрали. В свою очередь последнее определяется как

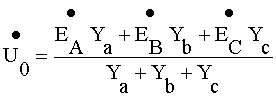
Фазные и соответствующие им линейные токи, а так же ток в нулевом проводе находим из следующих соотношений

A = Yaa ,B = Ybb , C = Ycc .

 При симметричной нагрузке, когда Ya=Yb=Yc напряжение смещения нейтрали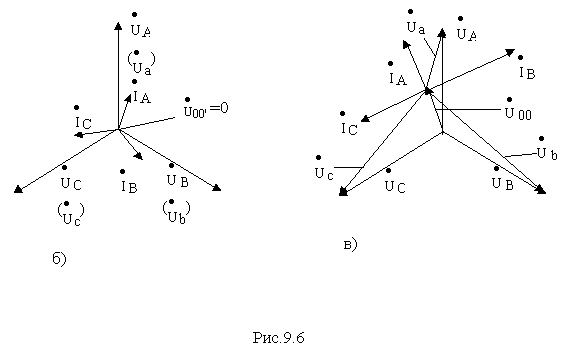 0=0 и фазные напряжения источника и приемника одинаковы, как и в четырехпроводной схеме (см. векторную диаграмму на рис. 9.6,б).

При несимметричной нагрузке, когда Ya№ Yb№ Yc напряжение смещения нейтрали 0№ 0 и фазные напряжения источника и приемника различны (см. векторную диаграмму на рис. 9.6,в).

Как видно при отсутствии нулевого провода изменение сопротивления одной из фаз приемника приводит к изменению напряжения 0 и, как следствие, к изменению фазных напряжений и токов других фаз.

Заметим, что при обрыве нулевого провода в четырехпроводной схеме несимметрия нагрузки приводит к несимметрии фазных напряжений и к взаимовлиянию фаз. Вот почему предохранители никогда не ставят в нулевой провод.

Мощность в трехфазной цепи

Трехфазная цепь является совокупностью трех однофазных цепей, поэтому ее мощность может быть определена как сумма мощностей фаз.

При соединении звездой активную P и реактивную Q мощности системы в общем случае можно определить как

P = Pa + Pb + Pc = UaIacosj a + UbIbcosj b + UcIccosj c =Ia2Ra + Ib2Rb + Ic2Rc ,

Q = Qa + Qb + Qc = UaIasinj a + UbIbsinj b + UcIcsinj c =Ia2Xa + Ib2Xb + Ic2Xc .

Если нагрузка соединена треугольником, то активная и реактивная мощности будут равны

P = Pab + Pbc + Pca = UabIabcosj ab + UbcIbccosj bc + UcaIcacosj ca =

=Iab2Rab + Ibc2Rbc + Ica2Rca ,

Q = Qab + Qbc + Qca = UabIabsinj ab + UbcIbcsinj bc + UcaIcasinj ca =

=Iab2Xab + Ibc2Xbc + Ica2Xca .

В частном случае симметричной нагрузки эти мощности равны соответственно

P = 3UфIфcosj ф =Ц 3UлIлcosj ф, Q= 3UфIфsinj ф =Ц 3UлIлsinj ф

Полную мощность можно определить из треугольника мощностей как

 

В частном случае симметричной нагрузки полную мощность можно найти по формуле

S=Ц 3UлIл

Следует обратить внимание на то, что полная мощность трехфазной цепи не является суммой полных мощностей фаз.