Лекция № 7.

ИНДУКТИВНО-СВЯЗАННЫЕ ЦЕПИ

При рассмотрении цепей гармонического тока до сих пор нами учитывалось явление самоиндукции, то есть явление наведения ЭДС в электрической цепи при изменении потокосцепления самоиндукции, обусловленного током в этой цепи. Для простейшей цепи, приведенной на рис. 7.1,а, при переменном напряжении на зажимах цепи справедливо уравнение Кирхгофа

,

где - напряжение, уравновешивающее ЭДС самоиндукции.

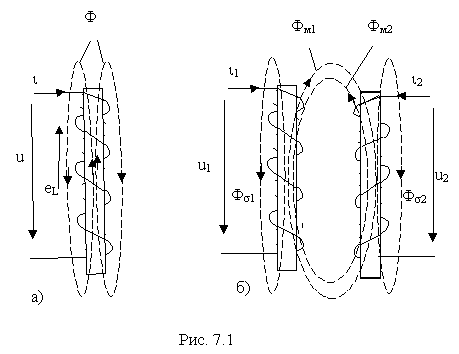
Физическая картина заключалась в следующем: переменный ток , протекая по виткам катушки создает переменный магнитный поток , который сцепляясь с витками катушки, обуславливает появление ЭДС самоиндукции eL, противодействующей по закону Ленца изменению потокосцепления , то есть

,

где - индуктивность, численно равная отношению потокосцепления самоиндукции к току, его обуславливающему.

Теперь рассмотрим явление взаимоиндукции, то есть явление наведения ЭДС в одной электрической цепи при изменении в ней потокосцепления, вызванного изменением тока в другой электрической цепи. Для этого проанализируем картину магнитного поля индуктивно-связанных катушек (рис. 7.1,б).

Протекание переменного тока по виткам первой катушки обуславливает появление магнитного потока Ф11. Часть этого потока сцеплена с витками только первой катушки и носит название потока рассеяния первой катушки Фs 1. Величина этого потока определяется формулой

,

где - магнитная проводимость пути, по которому замыкается поток рассеяния первой катушки.

Отношение

Y s 1/i 1=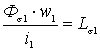

называется индуктивностью рассеяния первой катушки.

Часть потока пронизывает как витки первой катушки , так и витки второй катушки и носит название потока взаимоиндукции первой катушки , пронизывающего витки второй катушки. Таким образом,

Произведение является потокосцеплением второй цепи, обусловленное током в первой цепи.

Переменный ток , протекая по виткам второй катушки, создает переменный магнитный поток . Часть этого потока пронизывает только витки второй катушки и обуславливает потокосцепление рассеяния второй катушки

.

Отношение

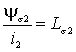
носит название индуктивности рассеяния второй катушки.

Часть потока , пронизывающая витки как первой, так и второй катушки, называется потоком взаимной индукции второй катушки, пронизывающим витки первой катушки .

Произведение

есть потокосцепление первой цепи, обусловленное током во второй цепи .

Связь потокосцепления взаимной индукции одной электрической цепи с током в другой цепи характеризуется взаимной индуктивностью . Взаимная индуктивность равна отношению потокосцепления взаимной индукции в одной цепи к току в другой цепи, то есть

,

.

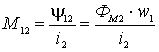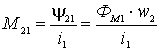Для линейных цепей всегда выполняется равенство , что легко показать. На самом деле

,

.

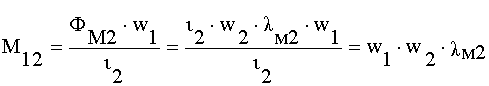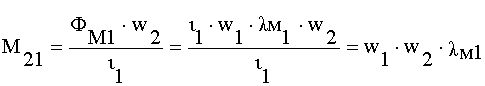где l м1иl м2 - магнитные проводимости путей, по которым замыкаются потоки взаимоиндукции ФМ1и ФМ2. А поскольку они замыкаются по одному и тому же пути, то l м1=l м2 =l м, то

М12= М21= М=w1w2l м.

Таким образом взаимная индуктивность пропорциональна произведению чисел витков катушек w1 и w2 и магнитной проводимости l м. пути потоков взаимной индукции, которая зависит от магнитной проницаемости среды, взаимного расположения катушек, их формы и размеров.

Степень индуктивной связи двух катушек характеризуется коэффициентом связи , определяемым как среднее геометрическое из отношений потока взаимной индукции к полному потоку катушки, то есть

.

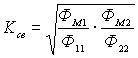Как видно, коэффициент связи всегда меньше , так как

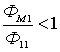и .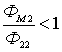

Коэффициент связи приближается к с уменьшением потоков рассеяния и . Повышение коэффициента связи достигается бифиляр-ной намоткой катушек и применением ферромагнитного сердечника, так как с увеличением магнитной проницаемости среды, по которой замыкаются потоки взаимной индукции, доля потоков рассеяния уменьшается.

Выразим потоки через токи катушек, числа витков, индуктивности и взаимную индуктивность следующим образом:

; ; ; .

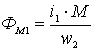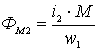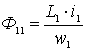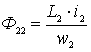Тогда

.

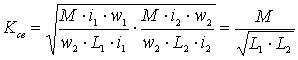ЭДС взаимной индукции

Если в отдельных индуктивных элементах цепи наводятся ЭДС взаимной индукции, то при расчете таких цепей необходимо учитывать напряжения, компенсирующие эти ЭДС. Сами эти напряжения uм21 , uм12, называемые напряжениями взаимоиндукции, как и напряжения на индуктивностях, пропорциональны скоростям изменения токов, их обуславливающих, т.е.

uм12=Mdi 2/dt, uм21=Mdi 1/dt.

Если токи i 1 и i 2 синусоидальны, то напряжение взаимоиндукции можно определить на основании закона Ома в комплексной форме. Так комплекс напряжения взаимоидукции второй катущки, обусловленного током первой катушки можно записать в виде

,

где ZM=jXM -комплексное сопротивление взаимоиндукции или сопротивление связи, а XM = w M -реактивное сопротивление взаимной индукции катушек. Таким образом, напряжение взаимоиндукции второй катушки опережает ток первой катушки на 90 градусов . Аналогично, напряжение взаимоиндукции первой катушки, обусловленное током второй катушки опережает ток второй катушки на 90 градусов , а комплекс этого напряжения определяется выражением

.

Согласное и встречное включение катушек

При расчете ЭЦ, где имеет место явление взаимоиндукции, учет этого явления производится путем включения в уравнения, составленные на основании второго закона Кирхгофа , дополнительных слагаемых в виде напряжений взаимоиндукции. Так для первой из катушек , представленных на рис. 7.1,б, уравнение Кирхгофа имеет вид

u1= uR1+ uL1 ± uм12.

Если напряжение на индуктивности первой катушки uL1 и напряжение взаимоиндукции uм12., обусловленные током второй катушки направлены одинаково , то перед последним слагаемым ставится знак (+), если противоположно - то (-). Указанные напряжения будут направлены одинаково, если поток самоиндукции первой катушки и поток взаимоиндукции, обусловленный током второй катушки , в первой катушке направлены одинаково. Аналогично

u2= uR2+ uL2 ± uм21.

В тех случаях, когда картина магнитных потоков катушек непосредственно не рассматривается, при расчетах условились ставить знак (+) перед последним слагаемым в случае , когда катушки включены согласно и знак (-) -когда они включены встречно.

Катушки считаются включенными согласно, если токи в них ориентированы одинаково относительно некоторых зажимов, помеченных на схеме цепи точками или звездочками и называемых одноименными и встречно, если они ориентированы противоположно.

Зажимы катушек считаются одноименными, если одинаково ориентированные относительно них токи, обуславливают одинаково направленные в катушках потоки самоиндукции и взаимоиндукции.

Физически направления магнитных потоков в катушках определяется правилом правоходового винта. Например, потоки Фм1 и Фм2 на рис. 7.2,а направлены

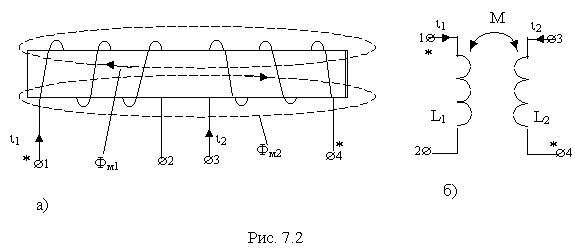
противоположно при заданных направлениях токов i 1 и i 2 , т.е. катушки включены встречно. Однако, если бы эти токи были ориентированы одинаково относительно зажимов соответственно 1 и 4, то потоки были бы направлены одинаково. Следовательно, эти зажимы можно считать одно-именными.

На рис. 7.2,б изображена эл. схема, соответствующая рисунку 7.2,а, где

наличие индуктивной связи между катушками показано дугой с стрелками, над которой стоит символ "М", а одноименные зажимы помечены символами (*).

Расчет цепей синусоидального тока с последовательно-соединенными и индуктивно-связанными катушками

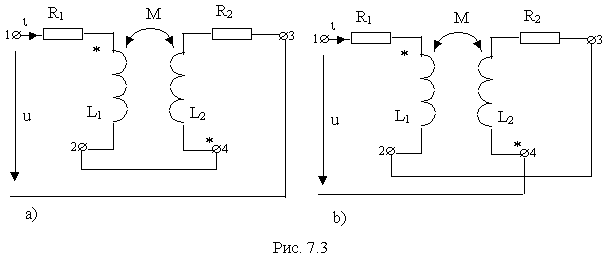
Схема цепи, подлежащей расчету приведена на рис. 7.3. Пусть известны параметры катушек , , , и взаимная индуктивность и требуется определить ток в цепи .

Положим вначале, что катушки включены согласно. Тогда на основании второго закона Кирхгофа для рассматриваемой цепи можно написать уравнение для мгновенных значений токов и напряжений в виде

.

Если напряжение на зажимах цепи синусоидально, то указанное уравнение можно записать в комплексной форме

.

Следовательно, комплекс тока в цепи определяется выражением

,

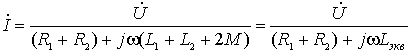где Lэкв=L1+L2+2M - эквивалентная индуктивность цепи.

Таким образом, две индуктивно-связанные катушки, соединенные последовательно при согласном включении эквивалентны катушке, имеющей активное сопротивление и индуктивность . Как видно индуктивная связь между катушками в данном случае увеличивает эквивалентную индуктивность цепи.

Пусть теперь катушки включены встречно. Тогда

.

Следовательно

,

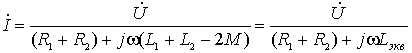где - эквивалентная индуктивность цепи.

Таким образом, наличие индуктивной связи между катушками при их встречном включении уменьшает эквивалентную индуктивность цепи .