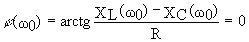text

Лекция 6

Резонансные явления в электрических цепях

Резонанс напряжений

Как отмечалось выше такой резонанс может иметь место в цепи, содержащей последовательно соединенные элементы R, L и С (рис. 5.1,а).

Если на некоторой частоте ω₀ в рассматриваемой цепи имеет место резонанс, то условием резонанса будет условие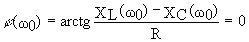

Последнее условие выполняется при равенстве X _L(w ₀)= X _c(w ₀)или w ₀L= 1/w ₀C. Следовательно, значение резонансной частоты w ₀можно определить через параметры элементов цепи следующим образом

w ₀=1/.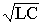

Сами значения реактивных сопротивлений на резонансной частоте носят название характеристического сопротивления резонансного контура и обозначаются обычно через r . Таким образом

X _L(w ₀)= X _c(w ₀)= r =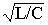 ,Ом.

Поскольку при резонансе реактивная составляющая комплексного сопротивления цепи равно 0, т.е. X(ω₀)=0, то комплексное сопротивление цепи Z₀ и полное сопротивление z₀равны активному сопротивлению, т.е.

Z₀=z₀=R.

Тогда действующее значение тока в цепи при резонансе зависит только от напряжения на зажимах U и активного сопротивления R, т.е.

I₀=U/z₀=U/R.

Действующее значение напряжения на активном сопротивлении равно действующему значению входного напряжения, т.е.

U_Ro=I₀R =U.

Отношение действующих значений напряжений на реактивных элементах цепи при резонансе к действующему значению входного напряжения определяются выражениями

;

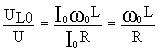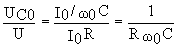
Отношение сопротивления реактивного элемента контура на резонансной частоте ω₀ к активному сопротивлению R называется добротностью последовательного резонансного контура.

Q= w ₀L/R=1/Rw ₀C.

Очевидно, что добротность контура равна отношению характеристического сопротивления к активному сопротивлению R, т.е.

Q=r /R.

Тогда U_Lo/U= U_Co/U=Q,

и, следовательно, действующие значения напряжений на реактивных элементах при резонансе равны по величине и в число раз, равное добротности контура, больше действующего значения входного напряжения Комплексы напряжений на реактивных элементах определяются выражениями

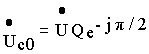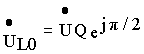
и, следовательно, последние сдвинуты по фазе друг относительно друга на 180 эл. градусов . Это показано на векторной диаграмме рис. 5.1,в.

Исследуем теперь частотные характеристики контура, т.е. зависимости действующего значения тока в цепи и фазового сдвига φ от частоты. Наибольшей общностью обладают характеристики, полученные в функции относительной частоты v =w /w ₀.

Осуществляя подстановку w =w ₀v в выражение (5.1) , определяющее ток в цепи, преобразуем его следующим образом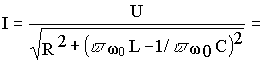

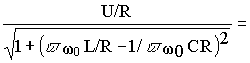
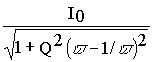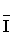
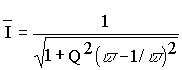После введения понятия относительного тока =I/I₀, окончательно получим

(6.1)

Осуществляя аналогичную подстановку в выражении (5.2) для фазового сдвига φ, οолучим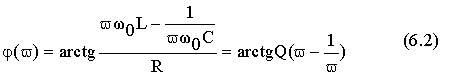

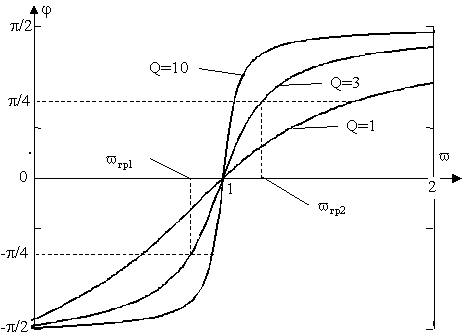
Семейство кривых, построенных по выражениям (6.1) и (6.2) приведено на рис. 6.1, а,б.

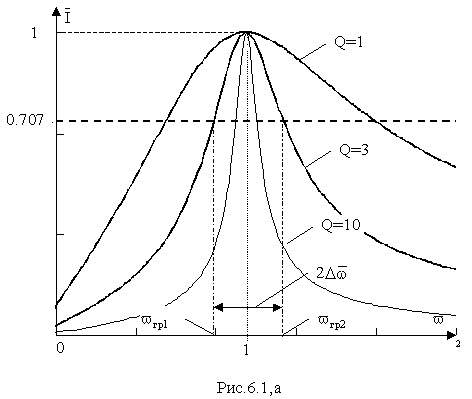
Исследование полученных зависимостей показывает, что:

а) При резонансе ток в последовательной R, L, C –цепи достигает максимума;

б) С ростом добротности контура кривые зависимости Ī(v ) становятся острее. Острота кривой Ī(v ) характеризуется полосой пропускания контура 2D v , опре-деляемой как разность граничных частот полосы пропускания v _2гр –v _1гр. Граничными частотами называются частоты, при которых ток в контуре умень-шается по амплитуде в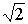 раз относительно своего резонансного значения Ī₀, т.е.

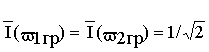или I(v _гр)=0.707I₀.

При достаточно больших добротностях Q полоса пропускания приближенно может быть определена из равенства

2D v = v _2гр-v _1гр=1/Q

в) На граничных частотах v _1гр и v _2гр полосы пропускания фазовый сдвиг между напряжением и током в цепи равен π/4. Крутизна кривых φ(ω) πΰстет с ростом добротности контура Q.

Резонанс токов

Как отмечалось выше такой резонанс может иметь место в цепи, содержащей параллельно соединенные элементы R, L и С (рис. 5.2,а).

Условием возникновения резонанса токов является равенство на некоторой частоте ω₀ емкостной и индуктивностей проводимостей, т.е.

1/ w ₀L =w ₀C.

Следовательно, значение резонансной частоты ω₀ можно определить по формуле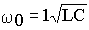

Поскольку при резонансе реактивная составляющая комплексной проводимости цепи равна 0, т.е. b(ω₀) = 0, то комплексная проводимость цепи Y и полная проводимость y равны активной проводимости g, т.е.

Y₀=y₀=g=1/R.

Тогда действующее значение тока в цепи при резонансе зависит только от напряжения на зажимах U и активной проводимости g, т.е.

I₀=Ug=U/R,

а действующее значение тока в резистивной цепи равно резонансному значению тока в цепи, т.е.

I_R0=Ug=U/R.

Отношение любой из реактивных проводимостей на резонансной частоте к активной проводимости называется добротностью параллельной R, L, C-цепи, т.е.

Q_T=R/w ₀L= Rw ₀C=R/r , где r =.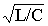

Тогда

Ic(w ₀)= Uw ₀C=I₀Q_T, I_L(w ₀)= U/w ₀L=I₀Q_T,

и, следовательно, действующее значение токов в ветвях с реактивными элементами при резонансе равны по величине и в число раз, равное добротности цепи, больше резонансного значения тока, протекающего через входные зажимы цепи I₀.

Комплексы токов в ветвях с реактивными элементами определяются выражениями

;

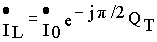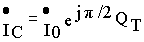
и, следовательно, последние сдвинуты по фазе друг относительно друга на 180 эл. Градусов. Это показано на векторной диаграмме (рис.5.2,в).

Исследуем теперь частотные характеристики цепи, т.е. зависимости тока в цепи и фазового сдвига между напряжением и током от частоты. Для этого jсуществим подстановку w =v w ₀ в выражениях (5.3) и (5.4). Тогда после пребразований получим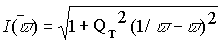

, (6.3)

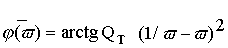. (6.4)

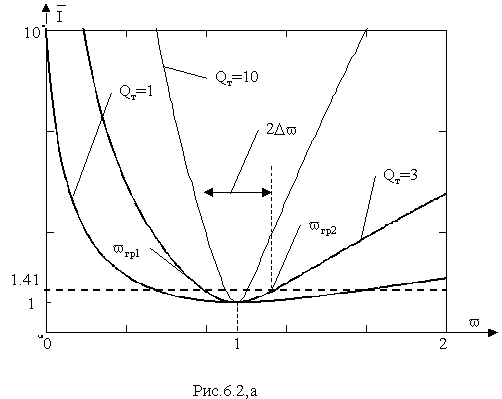
Кривые зависимостей I(v ) и φ( v )), построенные по выражениям (6.3) и (6.4) и приведены на рис.(6.2,а,б). Исследуя эти зависимости можно установить, что:

а) При резонансе ток, протекающий через зажимы параллельной R,L,C-цепи достигает минимума;

б) С ростом добротности Q_T кривые зависимости I(ω) становятся острее. Острота кривых характеризуется полосой пропускания, при достаточно больших добротностях определяемой приближенным соотношением

2D v = v _2гр-v _1гр=1/Q_т.

Граничными частотами полосы пропускания частот являются частоты, при которых ток, потребляемый цепью от источника, в √2 раз превышает свое резонансное значение.

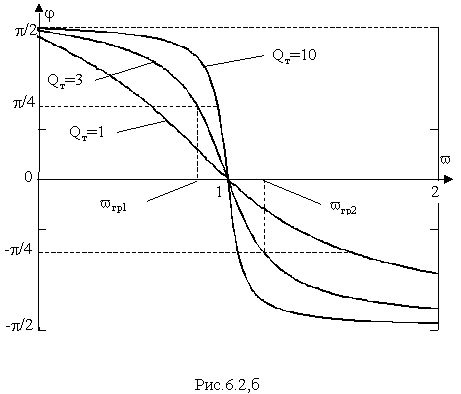
в) На граничных частотах v _2Гр и v _1Грполосы пропускания фазовый сдвиг между напряжением и током в цепи равен π/4. Крутизна кривых φ(v ) растет с ростом добротности цепи Q_T.

При резонансе токов, как и при резонансе напряжений, происходит непрерывный обмен энергией между индуктивностью и емкостью. Если бы параллельная цепь состояла бы только из элементов L и C, то при резонансе I₀=0 /т.к. g=0/ и ток от источника в цепь не поступал бы. Энергия, первоначально сообщенная контуру, не расходовалась бы и периодически бы перераспределялась между индуктивностью и емкостью. Такой колебательный контур является идеализированным, т.к. он не учитывает реальных потерь энергии в индуктивной и емкостной ветвях.

В действительности катушка индуктивности всегда обладает конечным активным сопротивлением r_K и наличие потерь энергии в сопротивлении r_K реальной катушке приводит к зависимости резонансной частоты ω₀ и добротности Q_T от величины сопротивления r_K .