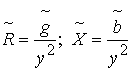
Лекция 5

Последовательная R,L,C- цепь

Пусть напряжение на входе цепи (рис.5.1,а) синусоидально, т.е.

u =Um Sin (w t+y u).

На основании второго закона Кирхгофа для данной цепи можно записать уравнение относительно комплексных амплитуд в виде

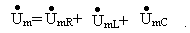
Зная комплексные сопротивления элементов цепи , на основании закона Ома в комплексной форме можно представить комплексные амплитуды напряжений на элементах так:

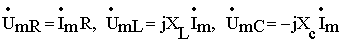
Тогда

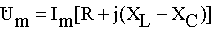
Находя отношение комплексных амплитуд напряжения и тока, получим комплексное сопротивление последовательной R,L,C- цепи в виде

Z =R +j (XL- Xc)

или

Z=,

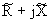где 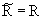- активная составляющая комплексного сопротивления,

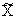= XL-Xc – реактивная составляющая комплексного сопротивления.

Следует заметить, что реактивная составляющая сопротивления цепи равна разности индуктивного и емкостного сопротивлений и поэтому может принимать разные знаки или обращаться в 0. Указанное обстоятельство является следствием того, что при протекании через реактивные элементы L и C одного и того же тока i напряжение на них uL и uc находятся в противофазе. Полное сопротивление контура

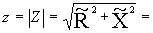
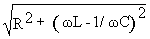
и, следовательно, амплитуда тока может быть определена как

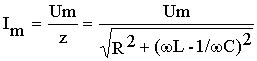
Аргумент комплексного сопротивления, определяющий фазовый сдвиг между напряжением и током, равен

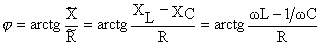
и, следовательно, выражение для мгновенного значения тока в цепи можно окончательно получить в виде

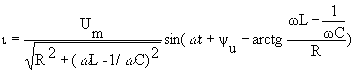
Таким образом, как амплитуда, так и начальная фаза тока зависят от соотношений индуктивного и емкостного сопротивлений, что иллюстрируется векторными диаграммами, приведенными на рис. 5.1,б, в, г.

Если X L > X c и, следовательно, UmL > Umc (рис.5.1,б), то j >0 и цепь носит индуктивный характер.

Если X L < X c и, следовательно, UmL < Umc (рис.5.1,в), то j <0 и цепь носит емкостной характер.

Если X L = X c и, следовательно, UmL =Umc (рис.5.1,г), то j =0 и цепь носит резистивный характер. В этом случае в цепи имеет место резонанс.

Параллельная R, L, C-цепь

Пусть напряжение на входе контура ( рис.5.2,а) синусоидально. На основании первого закона Кирхгофа для данной цепи можно записать уравнение относительно комплексных амплитуд тока в виде

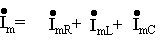
Зная комплексные проводимости ветвей цепи на основании закона Ома в комплексной форме можно представить комплексные амплитуды токов в ветвях так

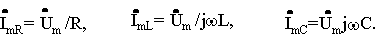
Тогда

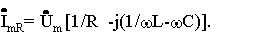
Находя отношение комплексных амплитуд тока и напряжениz, получим комплексную проводимость параллельной R, L, C-цепи в виде

Y=1/R-j(bL-bC)

или

Y=,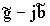

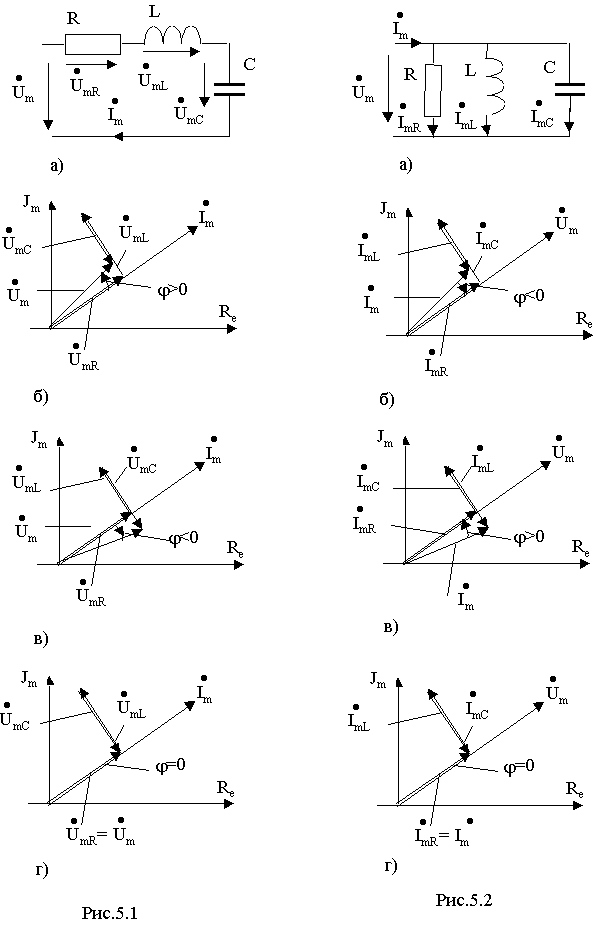
где 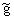=1/R - активная составляющая комплексной проводимости,

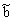=bL-bC - реактивная составляющая комплексной проводимости.

Реактивная составляющая комплексной проводимости рассматриваемой цепи равна разности проводимостей индуктивной и емкостной ветвей и поэтому может принимать разные знаки и обращаться при определенных условиях в 0. Указанное обстоятельство является следствием того, что при одинаковом напряжении на индуктивности и емкости токи, протекающие через эти элементы, находятся в противофазе.

Полная проводимость цепи

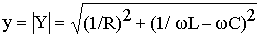
и, следовательно, амплитуда тока, протекающего через входные зажимы цепи, может быть определена как

.

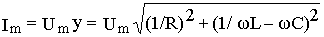Аргумент комплексной проводимости, определяющий фазовый сдвиг между напряжением и током находится по формуле

j =arctg(b/g)= arctg[R(1/w L -w C)]

и, следовательно, выражение для мгновенного значения тока в неразветвленной части цепи можно окончательно получить в виде

.

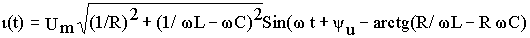Таким образом, как амплитуда, так и начальная фаза тока зависит от соотношения величин проводимостей индуктивной и емкостной ветвей, что иллюстрируется векторными диаграммами, приведенными на рис. 5.2 б, в, г.

Если bL < bC и, следовательно, ImL < ImC (рис. 5.2,б), то φ<0 и цепь носит емкостной характер.

Если bL >bC и, следовательно, ImL>ImC (рис. 5.2,в), то φ>0 и цепь носит индуктивный характер.

Если bL =bC и, следовательно, ImL=ImC ( рис. 5.2,г), то φ=0 и цепь носит резистивный характер. В этом случае в цепи имеет место резонанс.

Вообще в цепи, содержащей емкость и индуктивность, существует резонанс, если напряжение на зажимах цепи и ток, протекающий через зажимы, совпадают по фазе. В зависимости от схемы, по которой включены элементы R, L и C в цепях может иметь место либо резонанс напряжений, либо резонанс токов. При последовательном соединении указанных элементов в цепи имеет место резонанс напряжений, при параллельном- резонанс токов.

Эквивалентные преобразования пассивных двухполюсников

Как отмечалось ранее, ток напряжение на входе любого пассивного двухполюсника связаны между собой законом Ома в комлексной форме

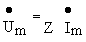 или ,

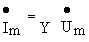где Z и Y- входные комплексное сопротивление и проводимость двухполюсника.

Входному комплексному сопротивлению Z=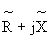 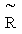соответствует эквивалентная схема двухполюсника, состоящая из последовательного соединения активного сопротивления и реактивного сопротивления 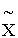(рис. 5.3,а). Последняя в зависимости от знака может быть либо индуктивной либо емкостной .

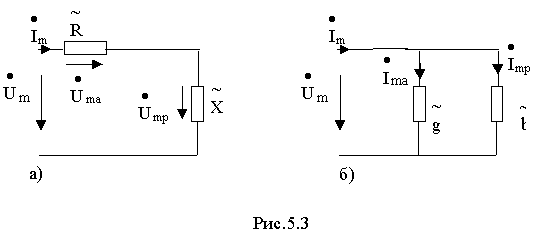
В соответствии с выражением

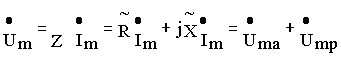
напряжение на зажимах такого двухполюсника можно разложить на 2 составляю-щие : активную 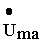, совпадающую по фазе с током, и реактивную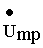, сдвинутую по фазе на угол p /2.

Входной комплексной провдимости Y=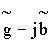 соответствует эквивалентная схема двухполюсника, состоящая из параллельного соединения активной провдимости 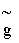и реактивной проводимости 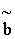(рис. 5.3,б). Последняя в зависимости от знака также может быть либо индуктивной либо емкостной .

В соответствии с выражением

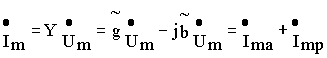
ток, протекающий через зажимы такого двухполюсника можно разложить на 2 составляющие : активную 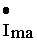, совпадающую по фазе с напряжением, и реактивную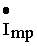, сдвинутую по фазе на угол p /2.

Переход от комплексного сопротивления Z к комплексной прово-димости Y и обратно соответствует замене схемы двухполюсника с последо-вательным соединением активного сопротивления 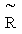и реактивного сопротивления 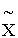схемой с параллельным соединением элементов 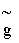и 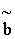и обратно. Схемы будут эквиваленты, если Y=1/Z, т.е.

.

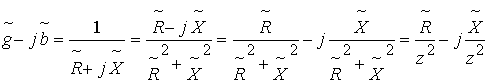Следовательно, .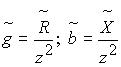

Обратный пересчет осуществляется по формулам