Лекция 4
Характеристики простейших пассивных двухполюсников в цепях синусоидального тока
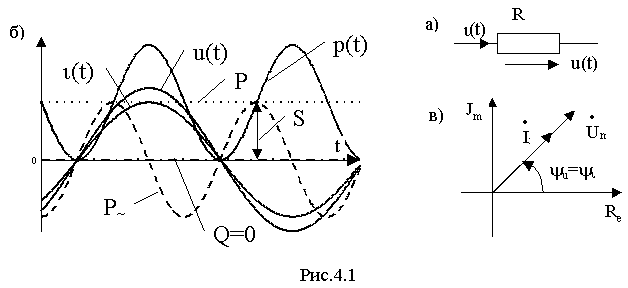
Пусть напряжение на резистивном элементе с сопротивлением R (рис. 4.1а,б) синусоидально, т.е. u(t)= U

Поскольку мгновенные значения напряжения и тока для резистивного элемента связаны законом Ома, то
i (t)= u(t)/ R= (Um/ R) Sin (w t+y u)или
i (t)= Im Sin (w t+y i ), где Im= Um/ R и y i =y u.Следовательно,
а) при синусоидальном напряжении на резистивном элементе ток в нем также синусоидален;
б) синусоидальные напряжения и ток совпадают по фазе (
j =y u-y i =0) (рис.4.1,б);в) амплитуда и действующее значение тока равны соответствующим значениям напряжения, деленным на R.
Мгновенная мощность в резистивном элементе определяется формулой
p(t)=u(t)
i (t)=UI- UICos2w t=p=+p~и иллюстрируется графиком на рис.4.1,б. Мощность пульсирует от нулевого значения до максимального, принимая только положительные значения. Это означает, что при любом направлении тока энергия поступает от источника в резистивный элемент и рассеивается в нем в виде тепла.
Средняя за период переменного тока (или активная) мощность равна
Р= p
== UI=I2R=U2g, Вт.Поскольку
j =0, то реактивная мощность равна 0, т.е. Q = UISinj =0.Полная мощность равна активной мощности, т.е. S=UI.
Находя отношение комплексной амплитуды напряжения к комплексной амплитуде тока , получим выражение для комплексного сопротивления резистивного элемента в виде
ZR=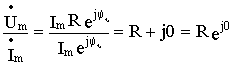 .
.
Следовательно:
а) комплексное сопротивление резистивного элемента содержит только активную составляющую ( реактивная составляющая равна нулю), т.е.
![]() ;
;
б) полное сопротивление резистивного элемента z=R;
в) аргумент комплексного сопротивления равен 0 (
j =0) и потому векторы напряжения на резистивном элементе и тока в нем совпадают по направлению ( рис. 4.1,в ) .Комплексная проводимость резистивного элемента есть величина обратная комплексному сопротивлению, т.е.
YR=1/ ZR= (1/R)ej0
=1/R, Сим.Следовательно:
а) комплексная проводимость резистивного элемента содержит только активную составляющую
![]() ;
;
б) полная проводимость резистивного элемента y=1/R;
в) аргумент комплексной проводимости равен 0 (
j =0).Пусть ток в индуктивном элементе с индуктивностью L (рис. 4.2а,б) синусоидален, т.е.
i (t)= Im Sin (w t+y i ).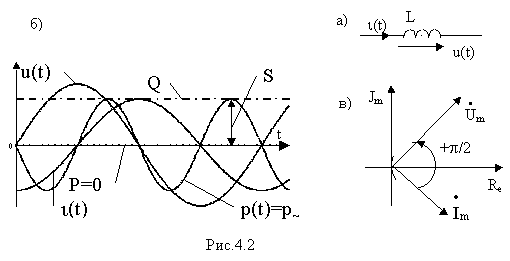
Поскольку мгновенные значения напряжения на индуктивном элементе пропорционально скорости изменения тока, то
u(t)=L d
i /dt= Imw L Cos (w t+y i )= Imw L Sin (w t+y i +p /2)или u(t)=U
mSin (w t+y u), где Um=Imw L –амплитуда напряжения и y u=y i +p /2- начальная фаза напряжения.Следовательно:
а) при синусоидальном токе в индуктивном элементе напряжение на нем также синусоидально;
б) напряжение опережает по фазе ток на угол
j =p /2 (рис.4.2,б);в) амплитуда и действующее значение напряжения равны соответствующим значениям тока, умноженным на величину
xL=
w L,Ом,называемую индуктивным сопротивлением.
Величина b
L, обратная индуктивному сопротивлению, называется индуктивной проводимостьюbL =1/ xL=1/
w L,Сим .Как видно, при неизменной амплитуде напряжения на индуктивном элементе с ростом частоты пропорционально падает амплитуда тока. Фазовый сдвиг между напряжением и током при всех частотах остается неизменным и равным
p /2.Мгновенная мощность в индуктивном элементе определяется формулой
p(t)=u(t)
i (t)=UISin2(w t+yi )=p~и иллюстрируется графиком на рис.4.2,б. Мощность содержит только переменную синусоидальную составляющую, меняющуюся с удвоенной частотой . На интервалах периода, когда знаки напряжения и тока совпадают, энергия поступает в индуктивность от источника, запасаясь в магнитном поле катушки. На интервалах периода, когда знаки напряжения и тока различны, энергия запасенная в индуктивном элементе возвращается обратно источнику.
Средняя за период переменного тока (или активная) мощность для индуктивного элемента равна нулю, т.е. Р= UICos(
p /2)=0.Поскольку
j =p /2, то реактивная мощность положительна и равнаQ = UISin
j =UI.Полная мощность равна по величине реактивной мощности, т.е. S=UI.
Находя отношение комплексной амплитуды напряжения к комплексной амплитуде тока , получим выражение для комплексного сопротивления индуктивного элемента в виде
ZL=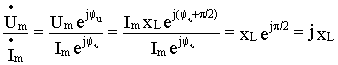
Следовательно
а) комплексное сопротивление индуктивного элемента содержит только реактивную составляющую ( активная составляющая равна нулю)., т.е. ![]()
б) полное сопротивление резистивного элемента z=x
L;в) аргумент комплексного сопротивления равен
p /2 (j =p /2) и потому вектор напряжения на индуктивном элементе опережает вектор тока в нем на p /2 ( рис. 4.2,в ) ;Комплексная проводимость индуктивного элемента есть величина обратная комплексному сопротивлению, т.е.
YL=1/ ZL= bLe-j
p /2=-jbL, См.Следовательно:
а) комплексная проводимость индуктивного элемента содержит только реактивную составляющую
![]() ;
;
б) полная проводимость индуктивного элемента y=b
L;в) аргумент комплексной проводимости равен -
p /2 (j =p /2).Пусть напряжение на емкостном элементе с емкостью С (рис. 4.3а,б) синусоидально, т.е. u(t)= U
m Sin (w t+y u).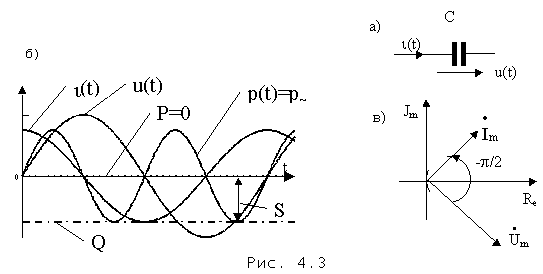
Поскольку мгновенное значения тока в емкостном элементе пропорционально скорости изменения напряжения, то
i
(t)=С du /dt= Umw C Cos (w t+y u)= Umw C Sin (w t+y u+p /2)или
i (t)= Im Sin (w t+y i ), где Im= Umw С –амплитуда тока и y i =y u +p /2)- начальная фаза тока.Следовательно:
а) при синусоидальном напряжении на емкостном элементе ток в нем также синусоидален;
б) ток опережает по фазе напряжение на угол
p /2 (j = -p /2) (рис.4.3,б);в) амплитуда и действующее значение тока равны соответствующим значениям напряжения, умноженным на величину
x
с=1/w С,Ом,называемую емкостным сопротивлением.
Величина bс, обратная емкостному сопротивлению называется емкостной проводимостью.
b
с =1/ xc=w C,СимКак видно, при неизменной амплитуде напряжения на емкостном элементе с ростом частоты пропорционально растет амплитуда тока. Фазовый сдвиг между напряжением и током при всех частотах остается неизменным и равным -
p /2.Мгновенная мощность в емкостном элементе определяется формулами
p(t)=u(t)
i (t)=UISin2(w t+yu )=p~и иллюстрируется графиком на рис.4.3,б. Мощность содержит только переменную синусоидальную составляющую, меняющуюся с удвоенной частотой . На интервалах периода, когда знаки напряжения и тока совпадают, энергия поступает в емкость от источника, запасаясь в электрическом поле конденсатора. На интервалах периода, когда знаки напряжения и тока различны, энергия запасенная в емкостном элементе возвращается обратно источнику.
Средняя за период переменного тока (или активная) мощность для емкостного элемента равна нулю, т.е.
Р= UICos(-
p /2)=0.Поскольку
j = -p /2, то реактивная мощность отрицательна и равнаQ = UISin
j = -UI.Полная мощность по величине равна реактивной мощности, т.е.
S=UI.
Находя отношение комплексной амплитуды напряжения к комплексной амплитуде тока , получим выражение для комплексного сопротивления емкостного элемента в виде
Z
с=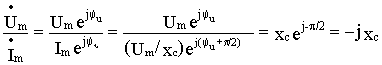 , Ом
, Ом
Следовательно
а) комплексное сопротивление емкостного элемента содержит только реактивную составляющую ( активная составляющая равна нулю). Таким образом для емкостного элемента
![]() ;
;
б) полное сопротивление емкостного элемента z=xс
;в) аргумент комплексного сопротивления равен -
p /2 (j =-p /2) и потому вектор напряжения на емкостном элементе отстает от вектора тока в нем на p /2 ( рис. 4.3,в ) .Комплексная проводимость емкостного элемента есть величина обратная комплексному сопротивлению, т.е.
Y
с=1/ Zс= bсejp /2=jbс, СимСледовательно
а) комплексная проводимость емкостного элемента содержит только реактивную составляющую
![]() ;
;
б) полная проводимость индуктивного элемента y=bс
;в) аргумент комплексной проводимости равен
p /2 (j = -p /2).Поскольку комплексные сопротивления и проводимости индуктивного и емкостного элементов содержат только реактивные составляющие, в литературе эти элементы часто называют реактивными элементами. Резистивный элемент, комплексное сопротивление и проводимость которого содержат только активные составляющие, называют активным сопротивлением.