Лекция 3

Задача анализа установившегося режима в ЭЦ синусоидального тока

Среди режимов работы ЭЦ различают установившиеся и переходные режимы. Установившиеся режимы имеют место в результате сколь угодно длительного воздействия источников энергии в ЭЦ. В ЭЦ с источниками постоянного напряжения и тока токи ветвей и напряжения на них неизменны во времени. В ЭЦ с источниками периодических напряжений и токов (синусоидальных и несинусоидальных) токи в ветвях и напряжения на них являются периодическими функциями времени.

Решение задачи анализа установившегося режима в ЭЦ с источниками синусоидального напряжения и тока во временной области сводится к отысканию частного решения системы дифференциальных уравнений, записанных по законам Кирхгофа для контуров и узлов ЭЦ. Но такой расчет для цепей с числом независимых контуров более двух связан с громоздкими выкладками, вызванными тем, что искомые начальные фазы токов находятся под знаком тригонометрических функций.

Поэтому для определения амплитуд и начальных фаз синусо-идальных напряжений и токов в установившемся режиме работы ЭЦ чаще применяют метод, предложенный в конце 19 века американским инжене-ром Чарльзом Штейнметцем и получивший название метода комплексных амплитуд . Все расчеты по этому методу осуществляются на основании алгебраических соотношений с использованием понятий комплексных амплитуд синусоидальных напряжений и токов, комплекс-ных сопротивлений и проводимостей элементов ЭЦ, законов Ома и Кирхгофа в комплексной форме.

Комплексные амплитуды и комплексы

При расчете этим методом всякой синусоидальной функции времени

A_mSin (w t+y ) ставится в соответствие комплексное число вида

=A_mе ^jy,

которое называется комплексной амплитудой синусоидальной величины. Как видно, комплексная амплитуда есть комплексное число, модуль которого равен амплитуде синусоидальной величины, а аргумент-начальной фазе. Как и всякое комплексное число комплексная амплитуда может быть представлена на комплексной плоскости вектором с длиной A_m и углом поворота относительно вещественной оси y . (рис.3.1)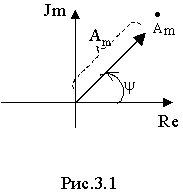

Во многих случаях пользуются понятием комплекса синусоидальной величины

=Aе ^jy,

т.е. комплексного числа с модулем в виде действующего значения синусоидальной величины и аргументом в виде начальной фазы.

Существует взаимно-однозначное соответствие между комплексной амплитудой и синусоидальной функцией времени. Например, мгновен-ныму значению напряжения u=25Sin(314t-30^o)B соответствует комплекс-ная амплитуда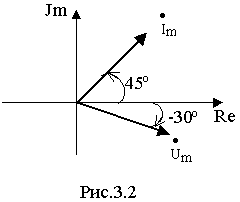 B и вектор на комплексной плоскости (рис.3.2).

Мгновенному значению тока i =10Sin(314t+45^o)B соответствует комплексная амплитуда B и вектор на комплексной плоскости (рис.3.2). Наоборот, зная комплексную амплитуду тока и частоту w , легко определить его мгновенное значение.

Примечание. Естественно, что масштабные коэффициенты при построении векторов тока и напряжения на комплексной плоскости могут быть разными.

Комплексное сопротивление и комплексная проводимость

Отношение комплексной амплитуды напряжения на зажимах двухполюсника к комплексной амплитуде тока, протекающего через эти зажимы, называется комплексным сопротивлением пассивного двухпо-люсника

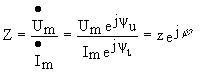Ом.

Модуль комплексного сопротивления, равный отношению амплитуды напряжения к амплитуде тока называется полным сопротивлением двухполюсника, т.е.

z=mod(Z)= U_m/ I_m ,Ом.

Аргументом комплексного сопротивления является фазовый сдвиг между напряжением и током на зажимах двуполюсника, т.е.

j = y_u -y_i .

Представляя комплексное сопротивление, как комплексное число, в алгебраической форме, получим

Z=z Cosj +j z Sinj = (Ом)

Вещественная и мнимая части комплексного сопротивления двухполюсника носят название соответственно активной и реактивной составляющих комплексного сопротивления.

Величина обратная комплексному сопротивлению называется комплексной проводимостью

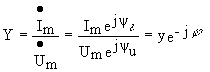Сим

Модуль комплексной проводимости, равный отношению амплитуды тока к амплитуде напряжения называется полной проводимостью двухполюсника, т.е.

y=mod(Y)= I_m/ U_m ,Сим.

Аргументом комплексной проводимости является фазовый сдвиг между напряжением и током на зажимах двуполюсника, взятый со знаком (-)

Представляя комплексную проводимость, как комплексное число, в алгебраической форме, получим

Y=y Cosj -j y Sinj =, Ом.

Вещественная и мнимая части комплексной проводимости двухполюсника носят название соответственно активной и реактивной составляющих комплексной проводимости.

Законы Ома и Кирхгофа в комплексной форме

Введение понятий комплексного сопротивления и комплексной проводимости означает, по-существу, введение закона Ома в комплексной форме для установившегося синусоидального режима

или .

Комплексная амплитуда напряжения на зажимах пассивного двухполюсника равна комплексной амплитуде тока, умноженной на комплексное сопротивление двухполюсника.

Пример 1. Через зажимы двухполюсника с комплексным сопротивлением Z=40e^j30 Ом протекает синусоидальный ток i =3 Sin (314 t + 15^o) A. Определить напряжение u(t) на зажимах двухпо-люсника.

Решение.

Находя комплексную амплитуду тока =3е ^j15 и зная комплексное сопротивление двухполюсника, на основании закона Ома в комплексной форме определяем комплексную амплитуду напряжения

=3е ^j15ґ40e^j30=120 е ^j45 В.

Следовательно, мгновенное напряжение равно u=120 Sin (314 t + 45^o), B.

Первый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.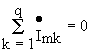

Поскольку каждое слагаемое в представленном выражении есть вектор, то результат есть сумма векторов. Это обстоятельсво позволяет контролировать аналитические расчеты наглядными графическими построениями-векторными диаграммами.

Пример 2 В узле ЭЦ сходятся 3 ветви с синусоидальными токам одной частоты (рис.3.3,а).

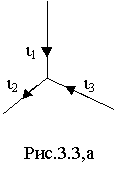
Мгновенные значения токов i ₂ и i ₃ определяются выражениями i₂= 100 Sin( 100t-45^o) и i₃= 50 Sin( 100t+30^o). Требуется определить ток i₁, пользуясь методом комплексных амплитуд.

Решение. На основании первого закона Кирхгофа в комплексной форме находим

I'_m1=I'_m2 -I'_m3 , где I'_m2=100e^-j45, I'_m3=50e^j30.

Тогда

I'_m1= 100e^-j45 - 50e^j30 = 100Cos45^o - j100Sin45^o -50Cos30^o -j50Sin30^o=

=27.4-j97.5=@ 101e^-j74A.

Построив вектора токов на комплексной плоскости (рис.3.3,б), убеждаемся, что сумма их действительно равна 0.

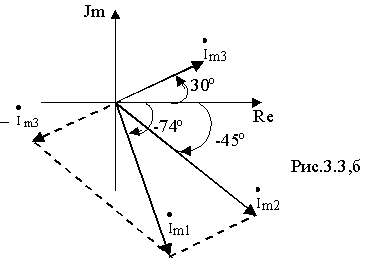
Переходя от комплекса к мгновенному значению, получим i₁= 101 Sin( 100t-74^o), А.

Второй закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом

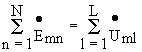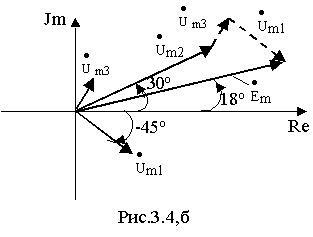
Пример 3. Известны мгновенные значения напряжений на элемен-тах контура ( рис.3.4,а) u₁= 10 Sin( 100t-45^o) B, u₂= 25 Sin( 100t+30^o)B, u₃= 5 Sin( 100t+60^o)B. Требуется определить мгновенное значение ЭДС источника напряжения.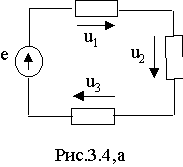

Решение. На основании второго закона Кирхгофа для мгновенных значений напряжений и ЭДС находим e= u₁+ u₂+ u₃.

Переходя к комплексам, получим , где

Следовательно,

10Cos45^o-j10Sin45^o+25Cos30^o+j25Sin30^o+5Cos60^o + j5Sin60^o =

=30.75+j9.75=@ 32.3e^j18в.

Построив вектора напряжений на комплексной плоскости (рис.3.4,б ) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e= 32.3 Sin( 100t+18^o), В.