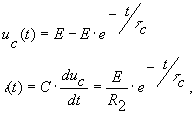
Лекция 12
При перебросе ключа К из положения 1 в положение 2 имеем
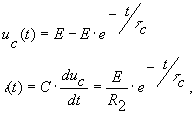
где
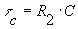
а при перебросе ключа К из положения 2 в положение 1
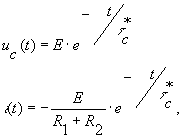
где :
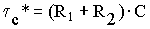
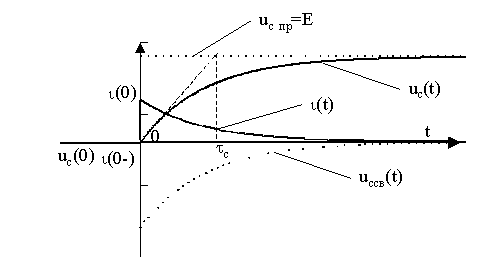
Временные зависимости uC(t) и ı(t), соответствующие процессам в рассматриваемой цепи, приведены соответственно на рис. 12.1,а, б.
 a)
a)
 б)
б)
рис. 12.1,а, б
Анализируя полученные зависимости, можно установить, что
а) при подключении RC-цепи к источнику напряжения и отключении ее от источника имеет место монотонный процесс изменения напряжения на емкости (заряда или разряда емкости);
б) в моменты коммутации (скачкообразного подключения или отключения источника) имеют место всплески (броски) тока в цепи емкости, величина которых зависит от суммарного сопротивления, включенного последовательно с емкостью. Следовательно, токи в ветвях с емкостями в переходном режиме во много раз могут превышать установившиеся значения;
в) время переходного процесса в RC-цепях первого порядка теоретически равно бесконечности. Практически принято считать переходный процесс закончившимся, если интересующая нас величина (напряжение или ток) достигнет 95% от своего нового установившегося значения. В этом случае время переходного процесса зависит от параметров R и C цепи, по которой происходит заряд или разряд емкости. Это время растет с ростом сопротивления R, поскольку последнее ограничивает величину зарядного или разрядного тока емкости. Увеличение емкости также приводит к росту времени переходного процесса, поскольку при неизменном напряжении на емкости с ростом емкости растет и энергия, которая в ней запасается;
г) практически время переходного процесса tпер" 3t С, где t С=R·C - постоянная времени последовательной RC-цепи. Постоянная времени t С численно равна времени, в течение которого свободная составляющая переходного процесса затухает в "е" раз. Постоянная времени графически может быть определена как длина подкасательной к кривой тока или напряжения в переходном режиме в любой момент времени. На рис. 12.1,а,б постоянные t С и t С* определены подкасательной к кривой напряжения uC(t) в момент коммутации (t=0).
2. Анализ переходных процессов в цепи первого порядка с индуктивным элементом (схема рис.11.1,б)
Процессы изменения тока в индуктивности и напряжения на индуктивности при подключении ее через сопротивление R2 к источнику напряжения протекает в соответствии с уравнениями
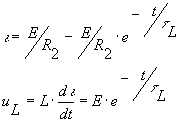
где
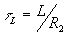
Для той же цепи) при перебросе ключа К из положения 2 в положение 1 уравнения, определяющие ток и напряжение на индуктивности, принимают вид
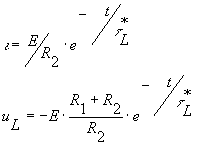
где
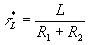
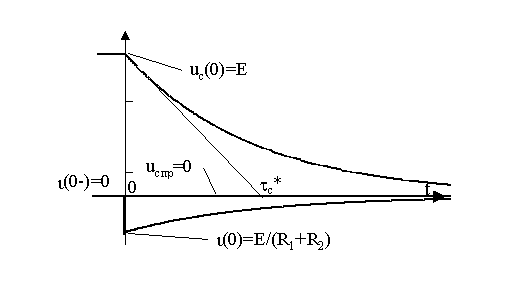
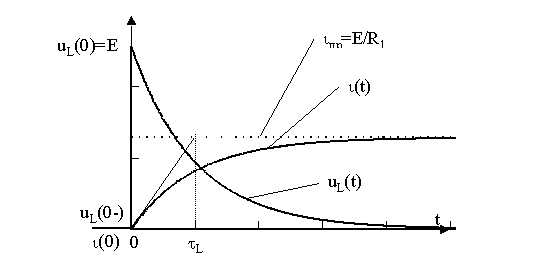
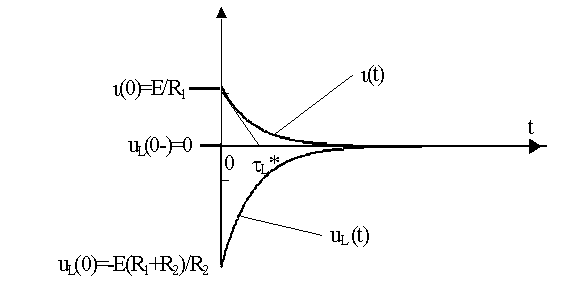
Графики полученных зависимостей приведены на рис. 12.2,а, б.
 а)
а)
 б)
б)
рис. 12.2,а, б
Анализ их показывает, что
а) при подключении индуктивности к источнику напряжения через сопротивление R2 и замыкании ее на сопротивления R1 и R2 при отключенном источнике имеет место монотонный (экспоненциальный) процесс изменения тока через индуктивность;
б) в моменты коммутации имеет место всплески (броски) напряжения на индуктивности, что может привести к возникновению перенапряжений на зажимах отдельных ветвей в цепях с индуктивностью при коммутациях. Величина всплесков напряжения при отключении цепи от источника зависит как от тока ι(0-) так и от сопротивления цепи, на которую замыкается индуктивность, (R1+R2);
в) практическое время переходного процесса зависит от постоянной времени t L цепи, так что tпер" 3·t L. Время переходного процесса растет с ростом индуктивности L и падает с ростом сопротивленияR, включенного последовательно с индуктивностью.
(схема рис.11.1,в)
В результате анализа переходного процесса в последовательной RLC-цепи можно установить, что характер переходного процесса зависит от параметров элементов цепи и может быть либо апериодическим, либо колебательным.
В случае если δ>ω0, переходной процесс носит апериодический характер, причем временные зависимости напряжения на емкости и тока в цепи определяется выражениями
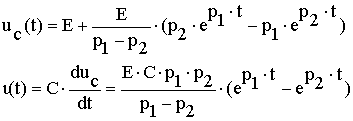
Графики зависимостей представлены на рис.12.3,а.
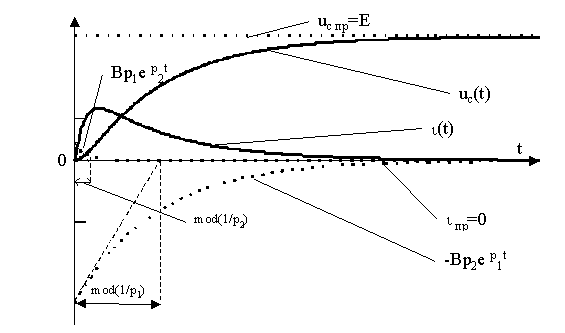
рис.12.3,а
Время переходного процесса в цепи определяется временем, в течение которого затухает самая медленная из экспоненциальных составляющих в свободной составляющей процесса uс св. Если предположить, что |p1|<|p2|, то в нашем случае медленнее затухает составляющая
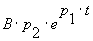 ,
,
где
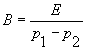 .
.
Случай d =w 0 соответствует предельному случаю апериодического процесса в рассматриваемой цепи и носит название "критического случая". Малейшее уменьшение сопротивления R или увеличение индуктивности L приводит к изменению характера свободной составляющей процесса (она становится колебательной). В "критическом случае" переходный процесс по характеру не отличается от рассмотренного выше и кривые напряжения на емкости и тока в цепи, определяемые соотношениями
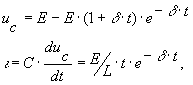
аналогичны соответствующим кривым, представленным на рис. 12.3,а.
В случае если d <w 0, корни характеристического уравнения цепи являются комплексно-сопряженными, кривые тока и напряжения на емкости определяются выражениями
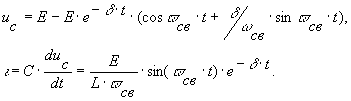
Эти кривые представлены на рис. 12.3,б и показывают, что в данном случае подключение источника напряжения к последовательной RLC-цепи обуславливает появление затухающего колебательного переходного процесса с частотой свободных колебаний w св и периодом Тсв = 2p /w св .
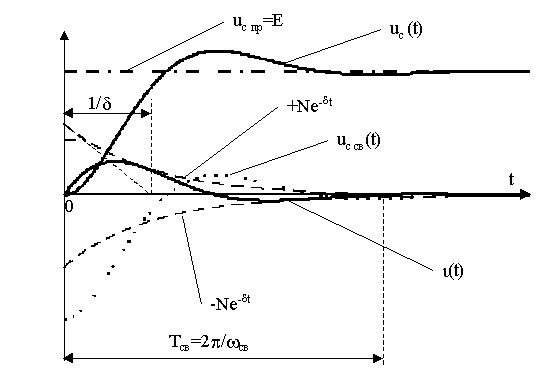
рис. 12.3,б
В процессе колебаний имеет место периодическое преобразование энергии электрического поля, запасаемой в емкости, в энергию магнитного поля, запасаемой в индуктивности. Это преобразование сопровождается необратимыми потерями энергии в резистивном элементе R , поэтому колебания являются затухающими во времени. Чем больше величина сопротивления R, тем быстрее затухают колебания во времени. Огибающими кривой тока ι(t) служат экспоненциальные кривые
±
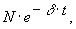
где
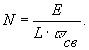
Величину 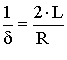 часто называют постоянной времени колебательного
контура, поскольку за время
часто называют постоянной времени колебательного
контура, поскольку за время 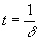 ордината огибающей уменьшается
(изменяется) в "e" раз.
ордината огибающей уменьшается
(изменяется) в "e" раз.
Чем меньше δ по сравнению с ω0 (чем меньше сопротивление R), тем медленнее затухают колебания и тем ближе частота свободных колебаний ωсв к резонансной частоте контура, определяемой соотношением
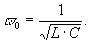
В предельном случае при R=0 имеем δ=0, ωсв=ω0. В этом случае в цепи будут иметь место незатухающие колебания с угловой частотой ω0, и говорят о контуре без потерь.
Относительное затухание колебаний характеризуется так называемым декрементом колебаний, представляющим отношение мгновенных значений тока через один период
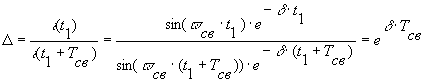
Декремент (затухание) колебаний не зависит от времени, так как отношение амплитуд в любом месте кривой тока имеет одно и тоже значение.
Натуральный логарифм декремента (затухания) колебаний называется логарифмическим декрементом колебания
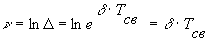
Все сказанное о частоте и затухании свободной составляющей тока относится также к свободным составляющим напряжений на емкости uс св и на индуктивности uL св.